离心泵转子系统在流体作用下发生振动变形的直接原因之一是作用在叶轮上的径向水力激振力。对于本章的单叶片模型离心泵而言，作用最明显的是由于单叶片流道内非对称流动与蜗壳隔舌间相互作用而产生的周期性水力不平衡力^[153]。这种水力激振力实际上是一种宏观上抽象整合出的合力，分析该合力有利于整体上理解转子水力激励振动现象的产生机理。该合力是由分散作用在叶轮叶片及前后盖板表面的流体压力（图4-25）和流体粘性作用力合成的，对这些分散的力在叶轮表面进行积分，见式（4-14）和式（4-15）^[148]。叶轮所受到的径向力即为压力径向力和粘性径向力向量的合力向量，且该合力向量为叶轮旋转位置或时间的函数，见式（4-16）。

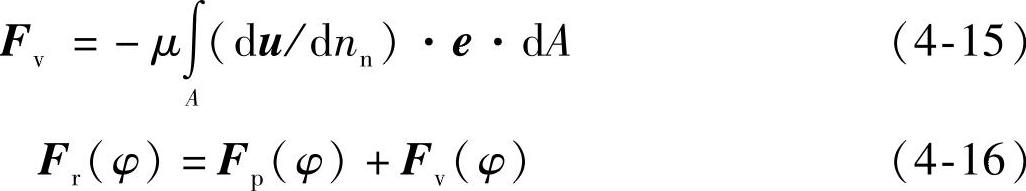
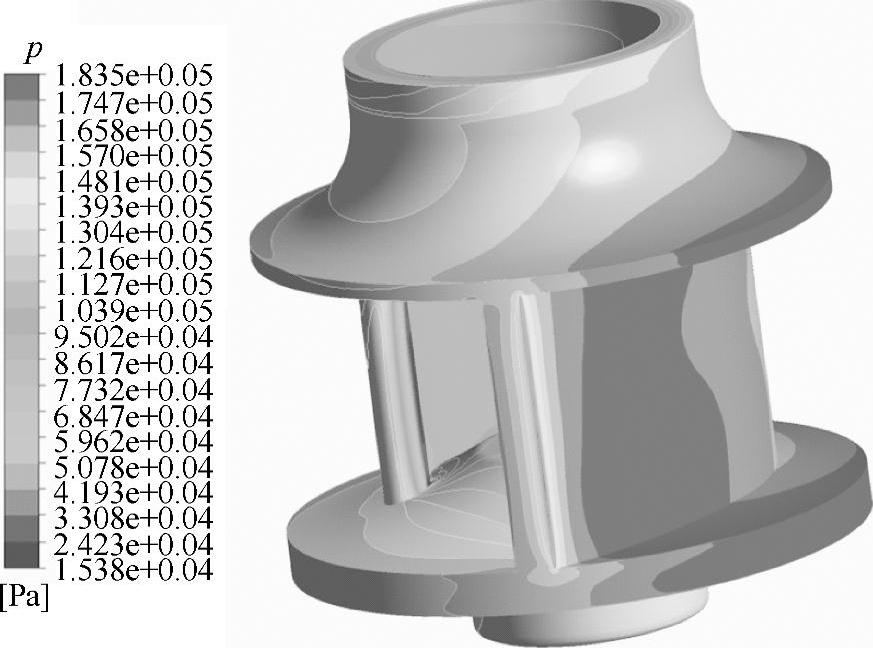
图4-25 单叶片离心泵叶轮典型流体压力分布

本书假设各径向力以及合力向量在径向平面上都等效作用于叶轮转轴的轴心点，即每个面单元上径向力分量都在该中心点进行向量求和，因此，在对叶轮求解径向合力时产生了流体力对叶轮结构的转矩作用。同时，通过实际的计算可知，相比于流体压力产生的径向力，流体粘性作用所产生的径向作用力相对较小，同时也忽略该粘性作用力，即流体对结构的影响主要是流体作用在结构表面的压力产生的。因此，式（4-16）可以简化为式（4-17）。

F_r（φ）=F_p（φ） （4-17）

如图4-26所示是额定转速下大流量工况（Q=42L/s）叶轮各流固耦合交界面所受的径向力，是旋转坐标系下的结果。从该图可以看出，作用在前盖板和叶片上的径向力位于旋转坐标系的第二象限内，且作用在叶片上的径向力明显大于作用在前盖板上的力：作用在叶片上的力在500～1000N的范围内变化，而作用于前盖板上的径向力在小于250N的范围内变化。作用于后盖板上的径向力较小，位于旋转坐标系内的第三象限，最大值约为100N。最终得出的径向合力曲线主要位于旋转坐标系的第二象限，x方向最大径向力分量可达1250N，y方向最大分量约为350N。通过以上分析可知，使叶轮发生径向振动的水力激励不仅包括流体作用于叶片的力，作用于前后盖板的力同样不能忽视，而作用于盖板的力不仅包含叶轮流道一侧的流动作用，还包括叶轮与泵体间隙内的流动作用。因此，对于流固耦合计算而言，为了保证对流体作用力的准确求解，必须同时考虑叶轮流道和叶轮泵体间隙内的流动效应，采用全流场的CFD计算方法。

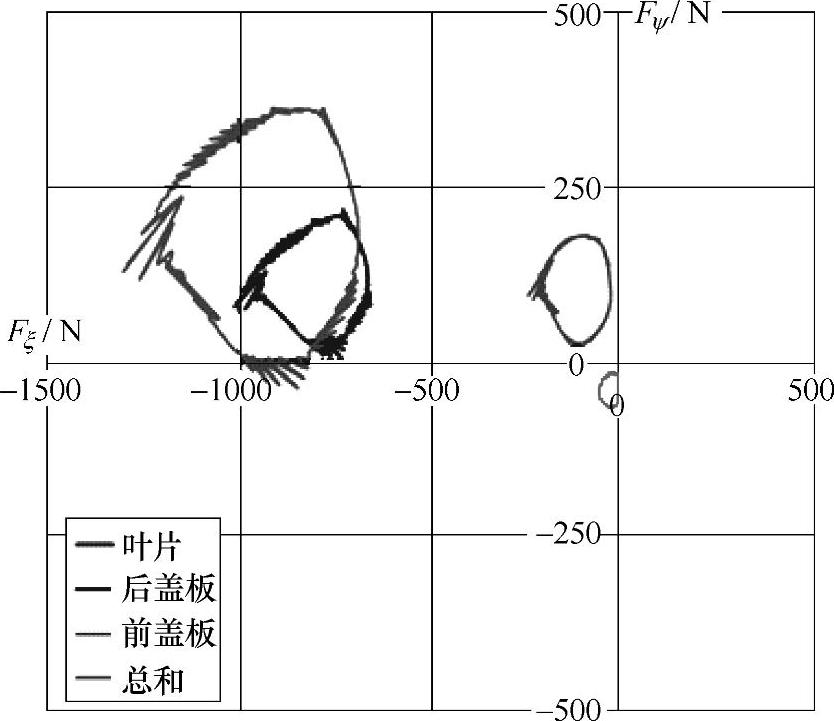
图4-26 额定转速Q=42L/s下叶轮各流固耦合交界面所受径向力在旋转坐标系下的结果

为了分析在各转速不同工况下模型离心泵叶轮所受径向力的相对大小，本章对不同转速定义了径向力大小参考值F_ref，见式（4-18），并对所求得的径向力值进行无量纲化换算。

如图4-27所示是额定转速下不同工况双向流固耦合求解得到的径向力，是静止坐标系下的表现形式，由旋转坐标系下的结果通过动静坐标系结果转换公式求得。从图中可以看出，径向力曲线呈椭圆形分布，曲线上出现的小波动主要是由流固耦合求解过程中数值不稳定性造成的，但该波动相对较小，已经通过前述的数值阻尼进行了控制，不影响整个计算结果的趋势。在静止坐标系下，第一、四象限内径向力大小差别不大，而在第二、三象限内径向力大小随着流量的增大而明显增大。此外，图中的箭头表示叶轮在φ=0°起始位置时径向力在静止坐标系下的分布位置。对于不同流量工况下的径向力，其相位也有一定差别，随着流量的增大，径向力起始点向逆时针方向移动。

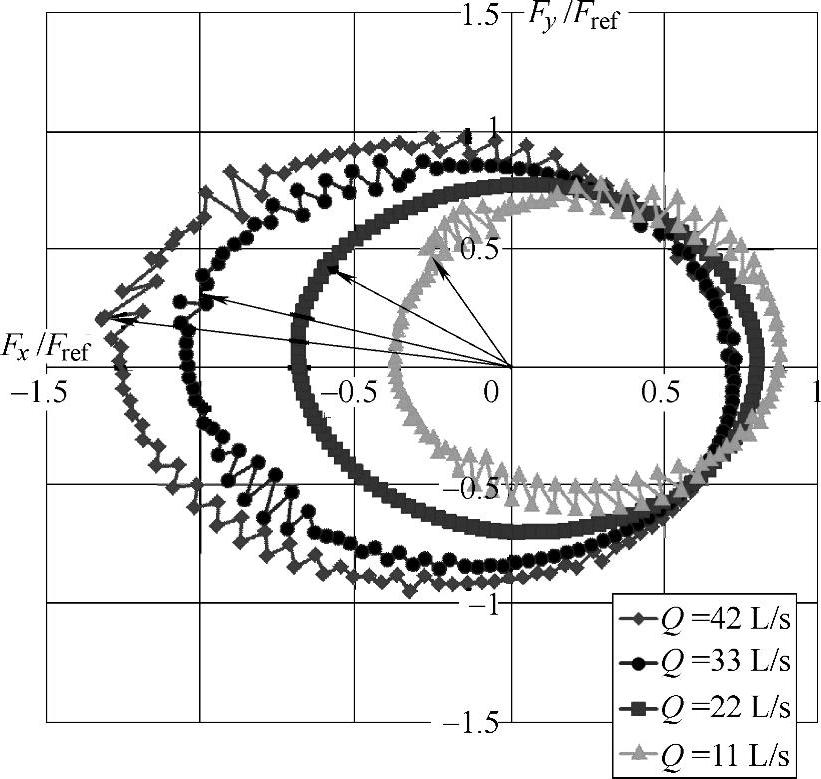
图4-27 额定转速下不同工况双向流固耦合求解径向力分布

同时也分析了低转速不同工况下双向流固耦合求解径向力分布情况，如图4-28和图4-29所示。从这两图中可以看出，其径向力分布曲线与额定转速下的结果有着近似的规律，如大小分布和相位分布。(www.daowen.com)

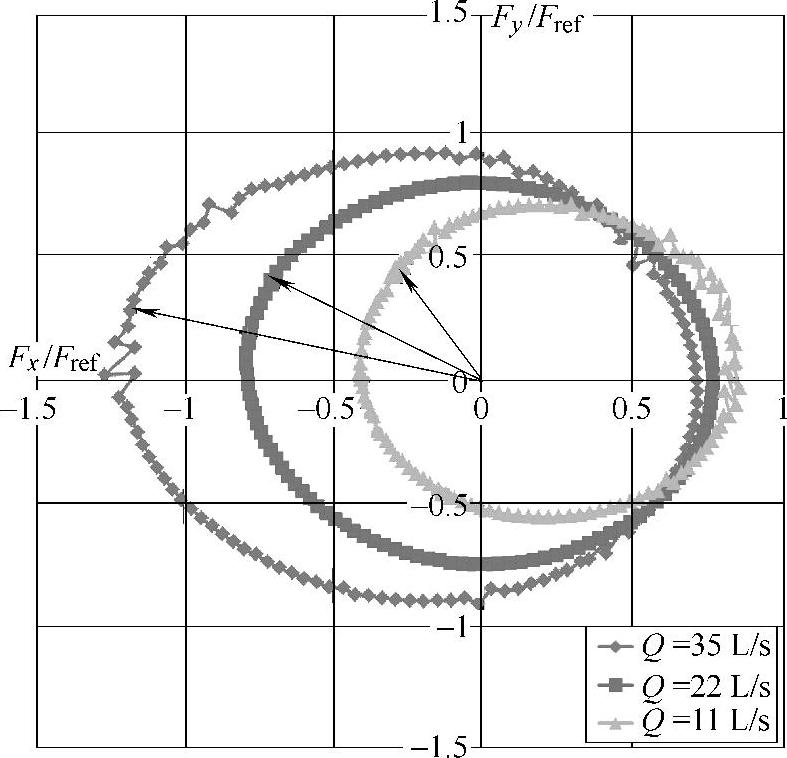
图4-28 n=1250r/min不同工况下双向流固耦合求解径向力分布

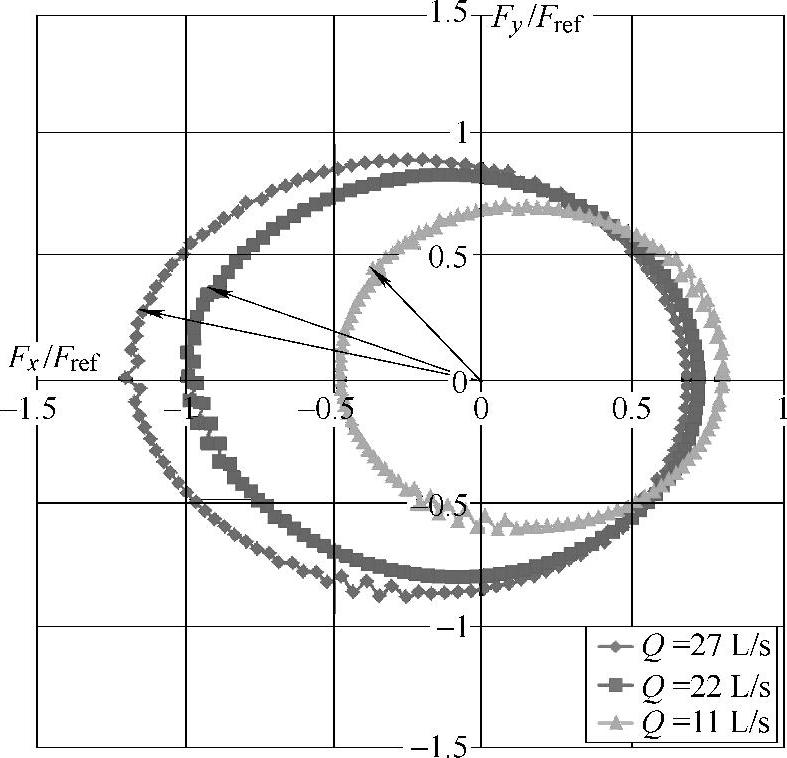
图4-29 n=1000r/min不同工况下双向流固耦合求解径向力分布

如图4-30所示是额定转速下各工况径向力在双向和单向耦合求解策略下的计算结果对比。从图中可以看出，两种耦合方式下得到的径向力大小结果没有明显的差别，仅单向耦合求解结果略小一些。在42L/s和22L/s流量工况下，两者存在一定的相位差。与双向耦合结果相比，单向耦合结果在大流量下存在一定的相位超前，而在小流量下相位滞后。此外，与双向耦合结果相比，由于单向耦合过程中流场不受结构振动的反作用，因此水力径向力结果更稳定。如图4-31所示是不同耦合求解策略求解相同网格的计算时间对比。该流固耦合计算使用的是4核工作站，单核运算速度为3.2GHz，计算采用HP MPI并行模式来获得高效的并行FSI求解。从图中可以看出，双向耦合求解所需时间明显多于单向耦合求解，这是因为双向耦合求解每时间步内包含若干的耦合迭代步。在

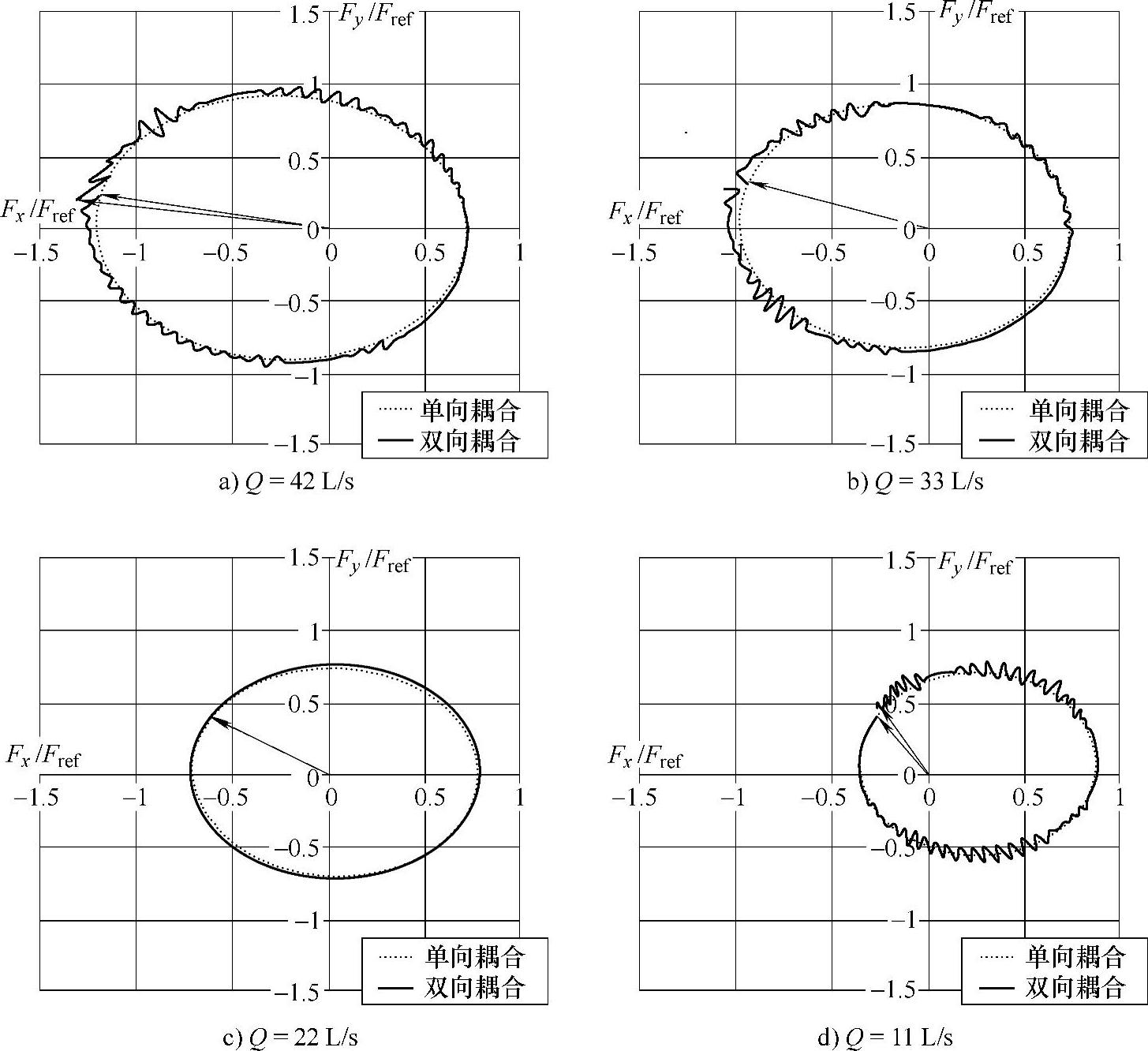
图4-30 n=1440r/min各工况下径向力求解策略下在单向和双向流固耦合计算结果对比

Q=33L/s工况下，计算时间差别最大，双向耦合计算时间约为单向耦合计算时间的4倍，这定量地给出了两种耦合方式的时间成本，为选取求解策略求解不同耦合问题提供参考。

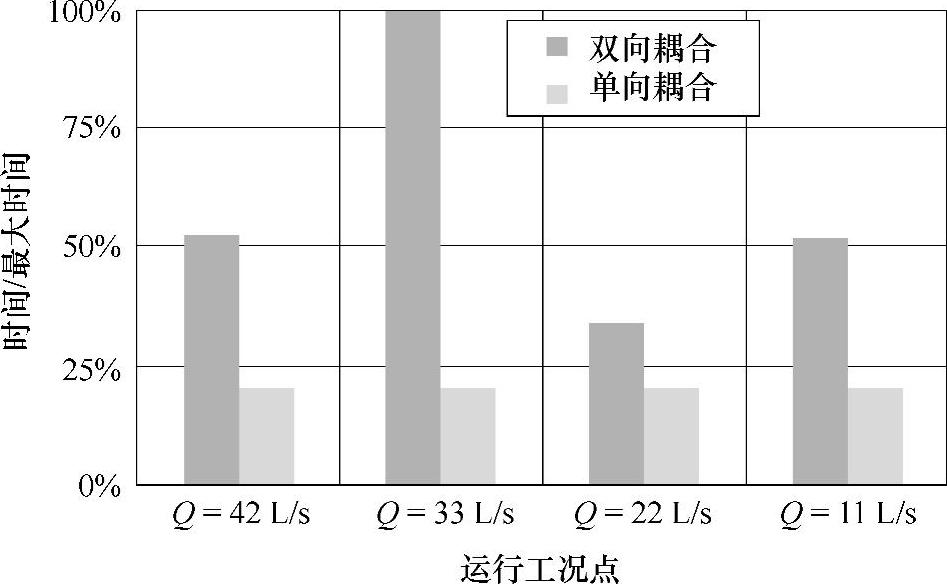
图4-31 n=1440 r/min各工况下不同耦合策略求解相同网格的计算时间对比

为了研究不同流体网格数对流固耦合求解的影响，本书在原有网格的基础上，选择了一个网格数较少的流体网格进行双向耦合求解，该网格节点数为185262，称为“粗网格，Coarse Mesh”，原有网格称为“细网格，Fine Mesh”。如图4-32所示，大流量工况下粗网格求解的径向力较小，并且有明显的相位差。在设计工况下，粗网格求解的径向力也较小，但相位差别不大。在Q=22L/s工况下，粗网格和细网格求解的径向力大小结果在整个叶轮旋转周期内都存在明显差别，但相位差别不大。对于Q=11L/s工况，粗网格求解结果在第一象限内较大，在其他象限内较小，相位差别不大。如图4-33所示是不同流体网格下耦合求解时间的对比情况。由于网格数较多，细网格耦合计算时间较长，但对于不同工况计算时间差别不同，最小差别出现在设计流量时，细网格计算时间约为粗网格计算时间的2倍。因此，进行流固耦合问题求解时，在保证流场求解精度相差不大的前提下，应考虑时间成本。

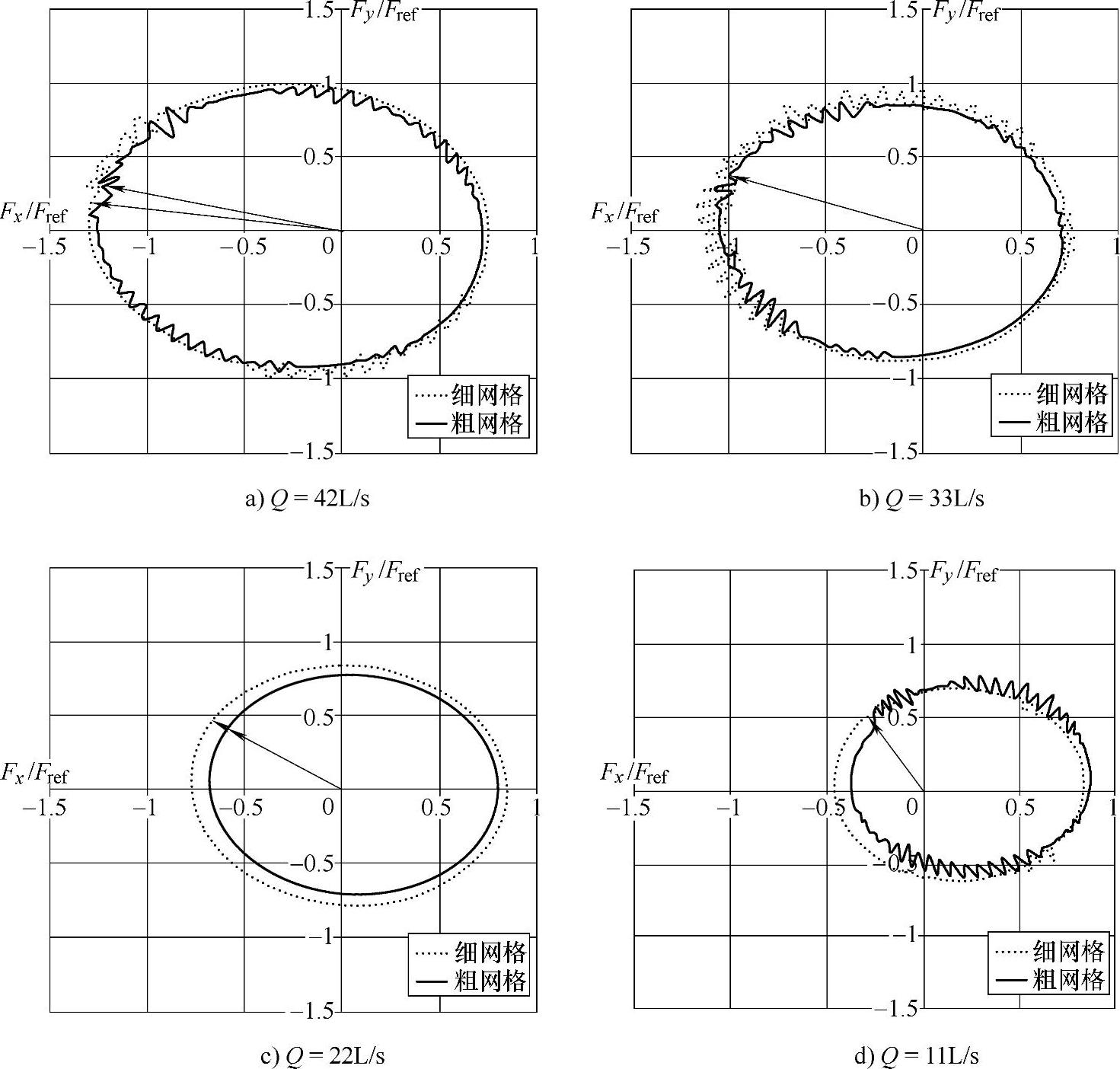
图4-32 n=1440r/min各工况下不同网格耦合求解径向力对比

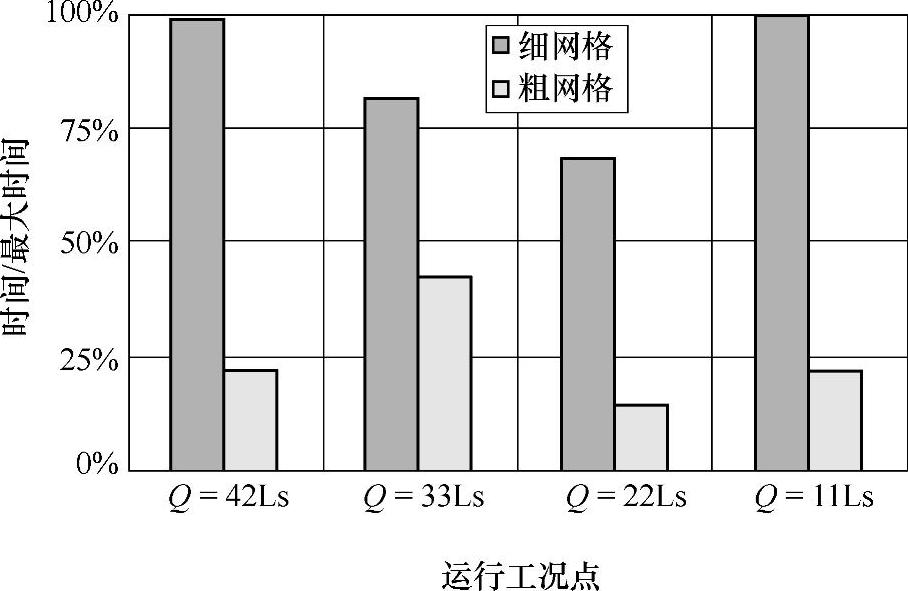
图4-33 n=1440r/min各工况下不同流体网格下耦合求解时间对比