基于ANSYS的模态求解已成功地应用在很多领域，包括旋转机械领域，且都取得了与试验模态吻合较好的结果，本书的模态分析是基于ANSYS的有限元计算方法。本节根据模态求解理论，针对本章中的单叶片叶轮有限元模型进行了求解。求解过程不加载预应力，仅在轴承安装处加载面约束。求解模式使用的是Direct方式，模态求解方法使用的是Block Lancos法。表4-3单列出的是求解得到的转子前6阶模态的固有频率。由该表可知，模型离心泵转子系统的第1阶固有频率为127.8Hz。

表4-3 模型离心泵转子系统前6阶模态的固有频率

根据模型离心泵的额定转速n=1440r/min，可由下式求得单叶片叶轮的叶片通过频率为：

(www.daowen.com)

可以得出结论，该单叶片离心泵内动静干涉作用的主要流体载荷频率远远低于转子系统的第1阶固有频率，因此该转子系统在动静干涉作用下不会发生共振现象。可以这样理解，与会使转子结构发生大变形的第1阶固有振动频率相比，动静干涉的流动载荷变化较慢，则可以将这时的结构动力响应问题简化为静力学响应问题，即结构响应随时间变化较慢，在计算时间步长内可以认为是静力学效应。如图4-24所示的额定转速Q=22L/s流量工况下动力学和静力学位移计算结果对比可以印证这一假设，从图中可以看出，转子系统在动力学和静力学情况下的结果十分相近。因此，可以得出结论，在本章的流固耦合计算过程中，结构振动的位移是影响流动分布的主要因素，而振动速度对流场的影响则可以忽略。同样的，在任何流固耦合计算过程中，需要首先对振动结构进行模态分析，分析出所研究的流体激励与结构自振频率间的关系，从而确定耦合计算中结构振动对流场影响的主要载荷传递量。

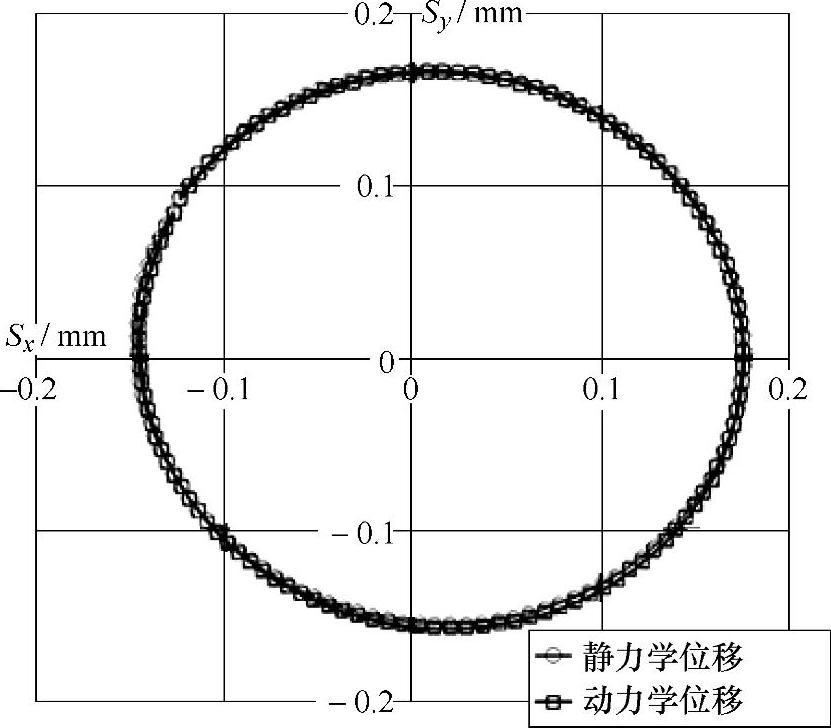
图4-24 额定转速Q=22L/s流量工况下动力学和静力学位移计算结果对比