结构的阻尼在系统动态响应分析中扮演着重要角色。由于各种阻尼的机理至今并不十分清楚，实际的阻尼矩阵不容易精确测定或计算出来，在工程实践中常将阻尼抽象为某种数学模型，根据与结构反应物理量等效的原则来确定其参数。阻尼不但与结构自身的物理特性有关，还与确定阻尼时的等效目标和分析方法有关^[164]。大量的分析研究表明^[161，162]，结构时程分析中阻尼模型和相应的阻尼比的选择还是一个很不明确的问题。本书采用试错法（Trial and Error）和相关的工程经验确定计算所使用的阻尼系数。

对多自由度结构，考虑阻尼的影响，并按粘滞阻尼理论，即假定阻尼的大小与质量振动的速度成正比，但方向与速度的方向相反。对于结构动力学运动方程（2-13），常用的假设是，阻尼矩阵C是质量矩阵M和刚度矩阵K的线性组合，其表达式为：

C=α·M+β·K （4-5）

这种阻尼称作瑞利阻尼。其中α和β分别为与质量成比例的系数和与刚度成比例的系数，即瑞利阻尼系数。α阻尼系数通常在系统连接处考虑，由于本计算中转子系统本身没有考虑连接，因此可以忽略该阻尼系数的影响，仅考虑β阻尼系数的影响。

图4-18 不同瑞利阻尼系数β对流固耦合振动位移结果的影响

如图4-18所示是不同瑞利阻尼系数β对流固耦合振动位移结果的影响。根据相关工程经验系数范围，β分别选择0.03%、0.1%和0.3%进行试算。从图中可以看出，β阻尼系数对于耦合计算结果的曲线形状和位置影响明显。当β取0.03%时，振动位移轨迹曲线出现不稳定现象，1个旋转周期内在坐标系每个象限均出现了1次波动，根据试验结果可知，该频率的波动是没有物理意义的；当继续增大刚度阻尼系数，β取0.1%时，计算结果稳定，曲线为平滑椭圆形；当β取0.3%时，计算结果仍是平滑椭圆曲线，仅曲线的位置发生了一定变化。由以上分析可知，随着β取值的增加，计算结果逐渐趋于稳定，因此，本书选择试算过程中使结果平稳的最小阻尼系数值作为计算的设定值，即β=0.1%。

为了保证流固耦合计算过程中的数值稳定性，除了瑞利阻尼系数的设置，ANSYS MFX耦合求解系统还提供了数值阻尼系数（Numerical Damping）。该系数没有实际物理意义，仅对数值计算过程有影响。为了将计算数据与试验结果进行对比并达到较高的精度，选取多个数值阻尼系数进行计算，并分析其对结果的影响，从而确定该系数值。(www.daowen.com)

如图4-19和图4-20所示是不同数值阻尼系数对流固耦合振动位移结果的影响。图4-19是数值阻尼系数在0.05～0.3区间的结果对比。从图中可以看出，在该阻尼系数区间内，计算结果随着阻尼系数的不同变化明显，且计算结果曲线有一定程度的波动，不同数值阻尼对结果曲线的影响也不同。图4-20是数值阻尼系数在0.4～0.9区间内的计算结果对比。由图可知，当数值阻尼系数增大到0.4时，计算结果已经变得稳定，且随着系数值的继续增大，结果变化不大，曲线近似为圆形。因此，本书根据以上试算的结果及分析，选取使计算结果稳定的最小数值阻尼系数0.4作为计算过程中的取值。

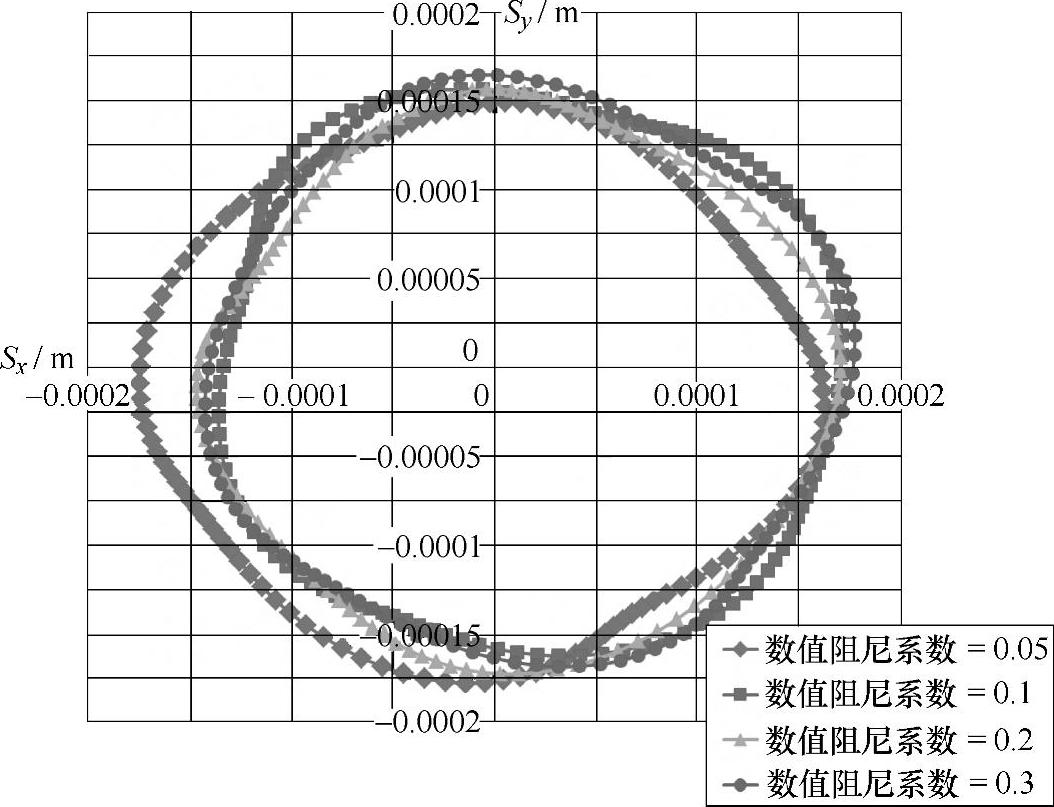
图4-19 不同数值阻尼系数对流固耦合振动位移结果的影响（0.05～0.3区间）

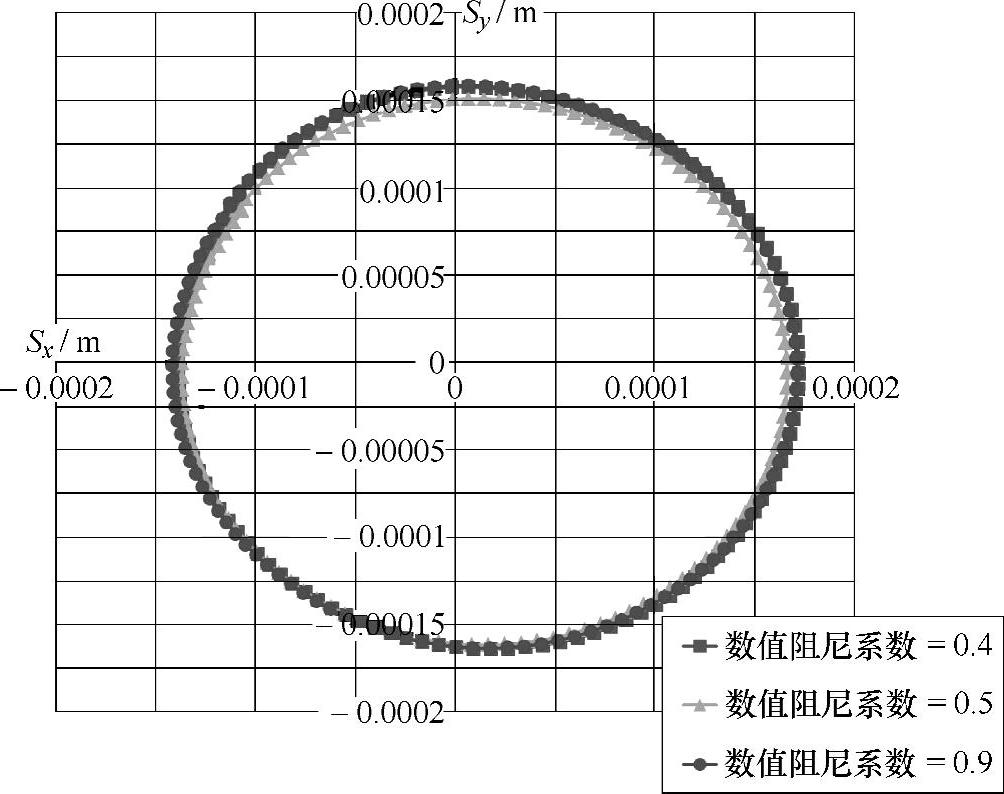
图4-20 不同数值阻尼系数对流固耦合振动位移结果的影响（0.4～0.9区间）

通过以上分析可知，两种阻尼系数的确定对最终的流固耦合振动计算结果影响十分显著，选择不当将会产生没有物理意义的错误结果。因此，阻尼系数是流固耦合计算中的关键参数之一，需要根据试验结果，利用试错法得到合理的取值。本计算最终得到的曲线是瑞利阻尼和数值阻尼同时作用的结果，得到的计算结果比较稳定。