ANSYS MFX求解流固耦合问题时使用的是多重坐标系方法，CFX中蜗壳区域是静止坐标系下求解的，而叶轮区域流场以及ANSYS中的叶轮结构求解是在同一坐标系，即旋转坐标系下进行的。这样构建计算的目的是保证叶轮流场网格能够与有限元网格进行实时数据传递。由于第3章离心泵叶轮瞬态水力激振试验测量结果是在绝对坐标系下，因此，为了便于将计算结果与试验结果进行对比分析，本节根据理论力学中的相对运动定理^[163]，提出了动静坐标系下流固耦合振动结果转换公式（4-3）和公式（4-4），后续所有绝对坐标系下的瞬态水力激振及径向水力激振力结果均由这两个公式换算。

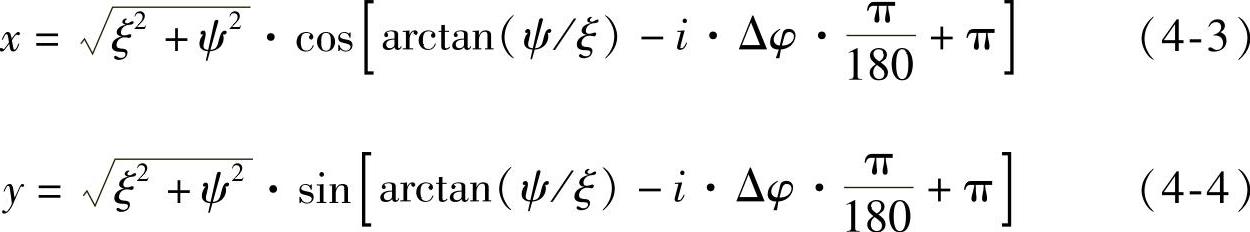
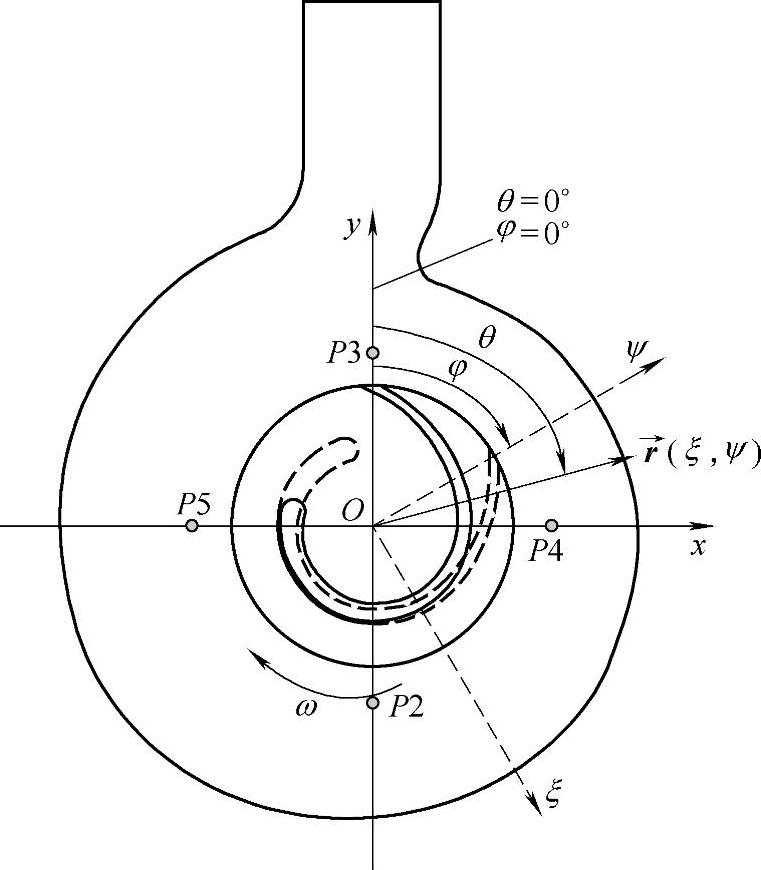
如图4-16所示是旋转坐标系下的结果向绝对坐标系下的结果转换的原理图。图中（ξ，ψ）代表旋转坐标系坐标；（x，y）代表静止坐标系坐标；i为时间步长数，且i=1，2，3…，120；Δφ为1个时间步长叶轮转动的角度，本书中Δφ=3°，公式中ξ≠0。对于旋转坐标系下各个象限内的（ξ，ψ）值，式4-3、式4-4均适用。设某一时间步长内旋转坐标系下的振动位移结果为（ξ，ψ），则可用式4-3、式4-4直接获得在绝对坐标系下的振动位移结果（x，y）。将1个叶轮旋转周期内每个时间步上的结果按上述两式进行转换，可得静止坐标系下1个旋转周期的振动位移结果。旋转坐标系下的振动位移结果向绝对坐标系下转换的效果如图4-17所示。

(www.daowen.com)

图4-16 旋转坐标系下的结果向绝对坐标系下的结果转换原理图

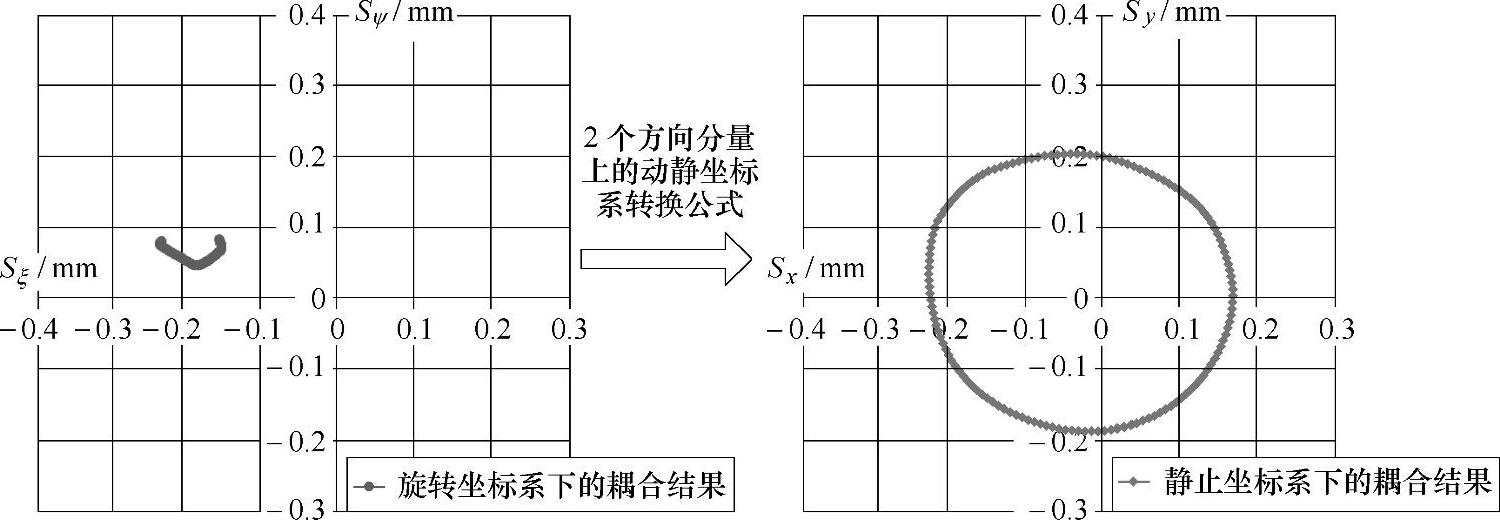
图4-17 旋转坐标系下的振动位移结果向绝对坐标系下转换的效果图