离心泵流固耦合数值计算的设置主要包括3个方面：流体CFD计算、结构FEM计算和耦合策略的相关参数设置^[161，162]。

1.流体CFD计算的相关设置

三维非定常雷诺时均Navier-Stokes方程的求解使用ANSYS CFX 12.1软件。进出口边界条件方面，进口设置为静止坐标系下的总压和流动方向，由试验测量的相关数据进行估算得出；出口边界条件设置为质量流量，由流量计测量并计算得出。定常计算采用k-ε湍流模型，交界面采用冻结转子（Frozen Rotor）设置，定常计算结果作为非定常计算的初始条件。非定常计算中，湍流模型采用SST（Shear Stress Transport）k-ε模型，湍流初始强度系数为5%。根据文献^[148]，流项离散格式的选择对计算的鲁棒性以及精度和收敛性有影响，且是相互制约的关系。一般可选取Blend Factor为0.75，但根据本书计算模型的情况，取该参数为1.0可以得到较好的计算稳定性以及精度。空间离散为二阶精度，时间离散选择二阶向后欧拉格式。转动区域和静止区域间的耦合面采用“瞬态转子-静子模型”，主要功能是捕捉瞬态转子和静子在相对运动过程中的相互作用情况。壁面设置为滑移壁面条件。所有计算区域的参考压力（Reference Pressure）设置为0Pa，则CFX求解得到的压力值即为绝对压力值。由于本计算的进出口边界条件完全依据试验值来设置，则计算时的工况与试验工况一致。CFX软件的计算采用独特的隐式欧拉时间离散方法，计算结果是数值稳定的，且对于时间步长的选择没有特殊限制。瞬态计算的时间步长根据每步叶轮旋转的角度确定，由式（4-1）计算。^[153]

式中，Δφ=3°，即1个叶轮旋转周期包含120个时间步长。

根据本书考虑的动静干涉作用结果频域范围可知，该计算精度完全可以满足对动静干涉作用非定常分量的捕捉。因此，对于额定转速n=1440r/min，时间步长为0.000347225s；转速n=1250r/min时，时间步长为0.0004s；转速n=1000r/min时，时间步长为0.0005s。此外，每个时间步长内的迭代收敛标准为最大残差（Maximum Residual）达到10^-3，每个时间步内设置最大迭代步数为10。典型非定常流场计算收敛残差曲线如图4-8所示。

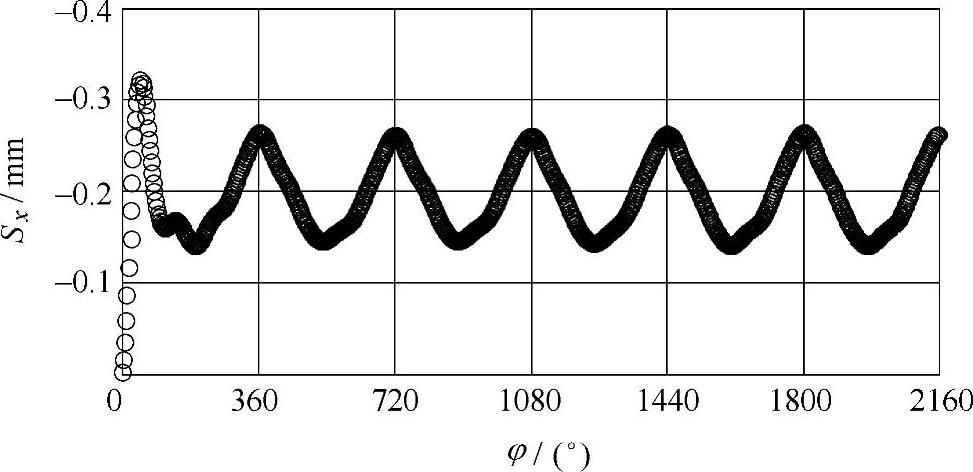
为了给流固耦合计算提供一个稳定的周期性初始流场，在耦合计算之前，先针对非耦合条件下的模型离心泵内流场进行非定常计算。本章的初始流场是模型离心泵叶轮旋转8圈的计算结果。同时，为了获得周期稳定的流固耦合计算结果，在初始流场的基础上，仍需对流固耦合计算进行多圈的耦合求解，总的耦合求解时间为6个叶轮旋转周期。典型的流固耦合求解叶轮结构振动位移结果曲线如图4-9所示。从图中可以看出，耦合计算在开始阶段出现不稳定波动，而后逐渐稳定，最终得到了稳定的周期性结果。因此，结果的分析是基于耦合计算第6圈的结果进行的。

2.结构有限元计算的相关设置

为了建立起流体计算和结构有限元求解之间的数据传递桥梁，在叶轮所有“湿”表面设置流固耦合交界面（Fluid-structure Interface），包括叶片、叶轮前盖板和后盖板，这其中也包含了前后盖板与泵腔内流动相对应的部分，如图4-6所示的区域。同时，定义图中区域为面固定约束边界条件（Face Fixed Support），即本书假定轴承为刚性，忽略轴

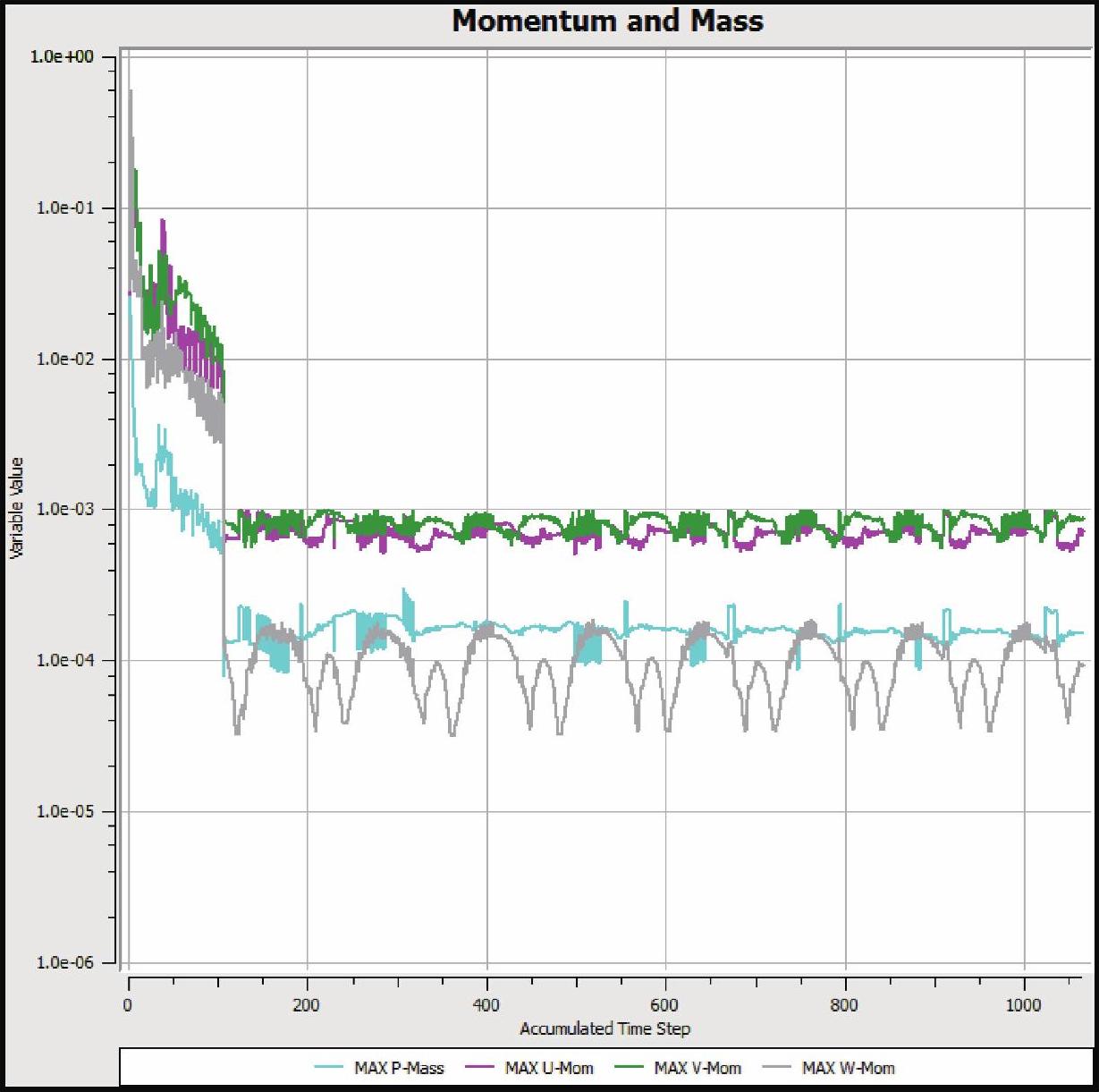
图4-8 典型非定常流动计算收敛残差曲线（Maximum Residual）

(www.daowen.com)

图4-9 典型流固耦合叶轮结构振动位移结果曲线

承的弹性。有限元时间积分采用Hilber-Hughes-Taylor（HHT）离散方法，使用瑞利阻尼（Rayleigh Damping）系数来定义结构瞬态阻尼效应。此外，定义数值阻尼系数来控制分块式载荷传递流固耦合求解系统的数值稳定性。所有的流固耦合计算结构方面的参数设置，包括有限元模型的数据以及流固耦合交界面节点编号，全部以ANSYS APDL程序语言的形式包含于*.inp文件。将此文件读入CFX程序并启动即可实现ANSYS FEM Solver与CFX Solver间的流固耦合计算。部分重要设置的APDL程序如下：

3.耦合系统相关参数的设置（双向耦合）

叶轮表面流固耦合交界面处的网格设为动网格（Mesh Motion），设置CFX从ANSYS求解器接收的数据类型为Total Mesh Displacement，CFX向ANSYS传递的数据类型为Total Force。为了控制耦合计算过程的收敛性，对所有两求解器间的数据传递过程设置合理的松弛因子（UnderRelaxation Factor），选择0.75；设置收敛准则为10^-2。每个耦合迭代步最大迭代步数设为200，最小步数设为1。通常情况下，流固耦合计算稳定后，数据过程会在10步以内收敛。设置ANSYS有限元的求解在CFX求解之后启动。流固耦合计算的收敛包括：每个时间步长内各迭代步中流场计算的收敛、每个时间步长内各迭代步中结构有限元求解的收敛和每个时间步长上的两求解器间的数据传递过程的收敛。由于流固耦合计算的初始流场条件已经是收敛较好且周期稳定的结果，且结构有限元计算的收敛性也较好，因此流固耦合计算过程中主要关注的是数据传递过程的收敛。双向耦合计算过程的收敛曲线如图4-10所示。由式（2-26）

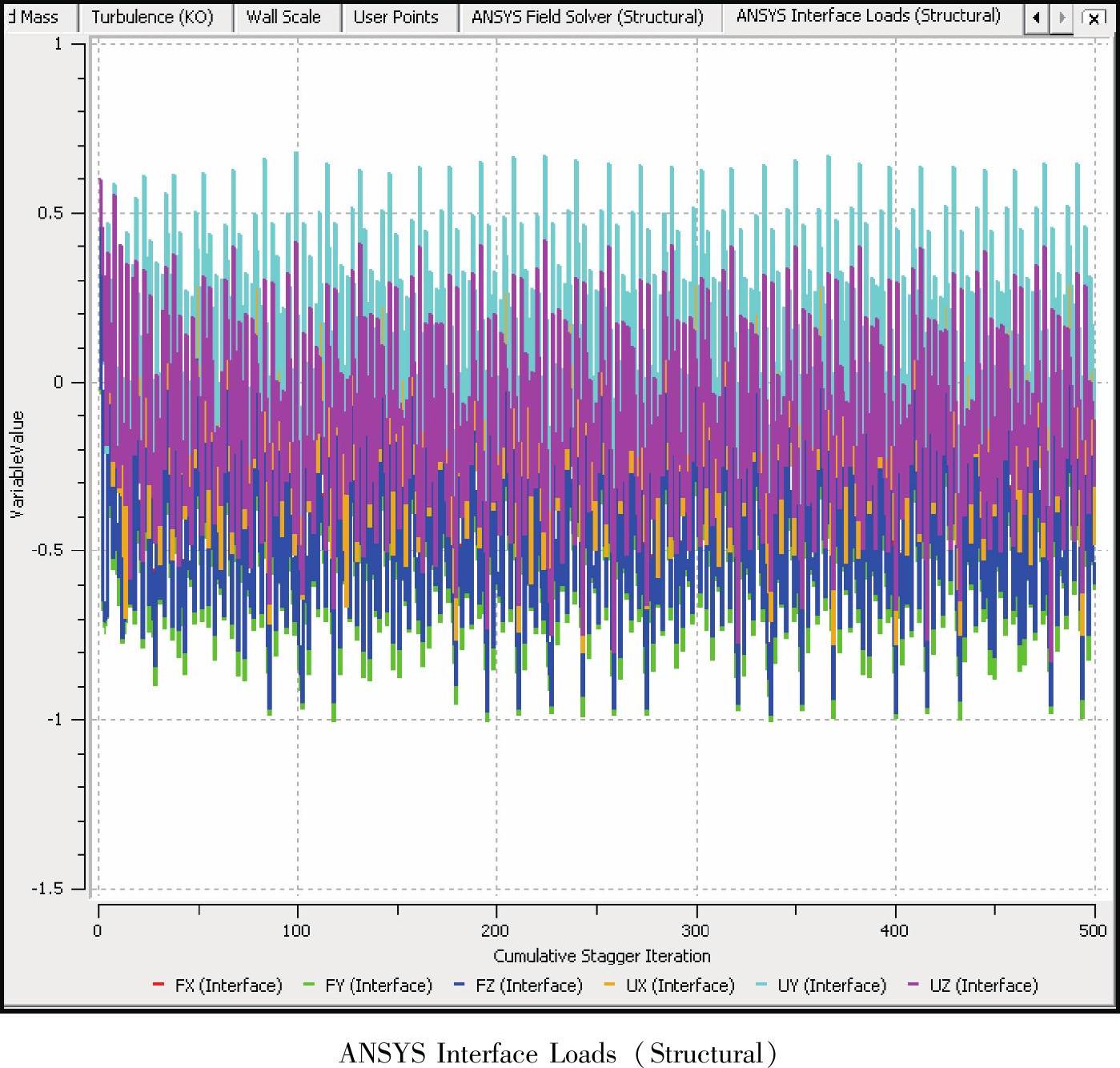
图4-10 双向耦合计算过程的收敛曲线

可知，每个时间步长内当所有值小于零时，则该时间步长内耦合计算收敛。