如前所述，本试验期望获得的是由离心泵内部动静干涉作用产生的周期性水力激振结果。为了获得周期性较好的结果，减小非周期性因素的影响，需要对大量测量得到的振动结果进行周期相平均计算。在实际测量过程中，由于离心泵的转速较难维持绝对恒定，会随着时间发生小幅变化，这就导致了实际运行时叶轮旋转每一周的时间都会有误差。即在采样率不变的情况下，叶轮旋转每一周，系统所采集的数据量也会不同。因此，在做相平均的过程中，无法对每个相位的数据进行对应平均计算，这使得相平均计算的误差增大。为了解决这一难题，本试验提出了新的相位处理方法，并基于LabVIEW编制了自动处理程序。

如图3-33所示是本书使用的相平均处理程序图，试验给出的均是对50个叶轮旋转周期进行相平均后的最终结果。当n=1440 r/min，采样频率为10000Hz时，1个叶轮旋转周期内的采样点数为416；当n=1250r/min时，旋转周期内采样点数为480；当n=1000r/min时，旋转

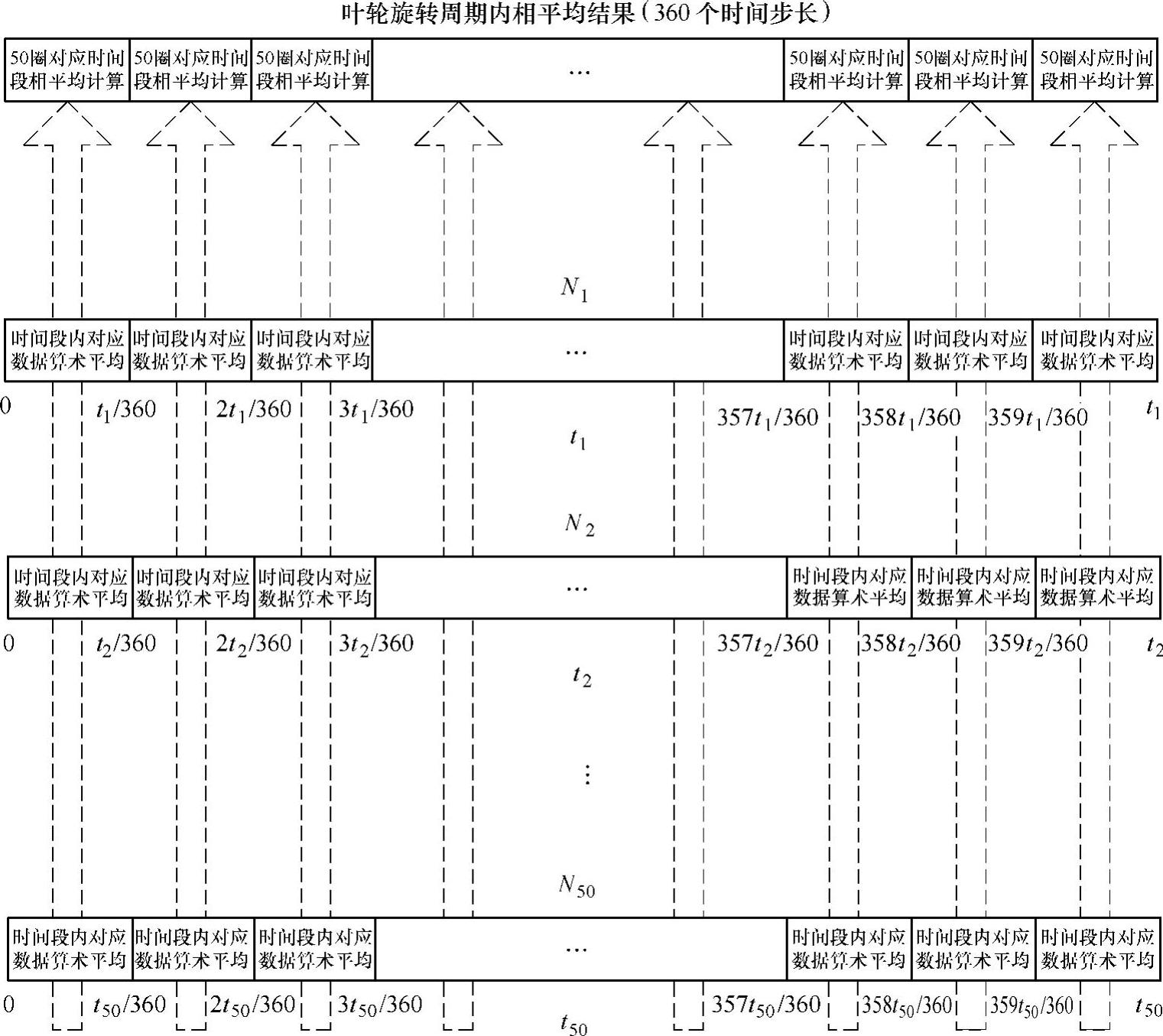
图3-33 相平均处理程序图

周期内采样点数为600。由于实际测量中转速无法保证绝对的恒定，因此测量得到的每个叶轮旋转周期略有差别，即图中给出的叶轮旋转周期t₁，t2，…，t50各不相同，从而导致每个周期内的数据采集量N₁，N₂，…，N50也各不相同。人为地将各个旋转周期平均分成360个时间段，将每一时间段内对应的测量值进行算术平均，计算结果作为该时间段的测量值，最终可使用360个值代表整个旋转周期内的测量结果。无论每个周期内的数据采集量是否相同，最终每个周期结果都被转换为相同的360个相位对应的结果，进而对50个周期对应的相位结果再进行平均，得到相平均结果。如图3-34所示是本书使用的相平均处理程序。

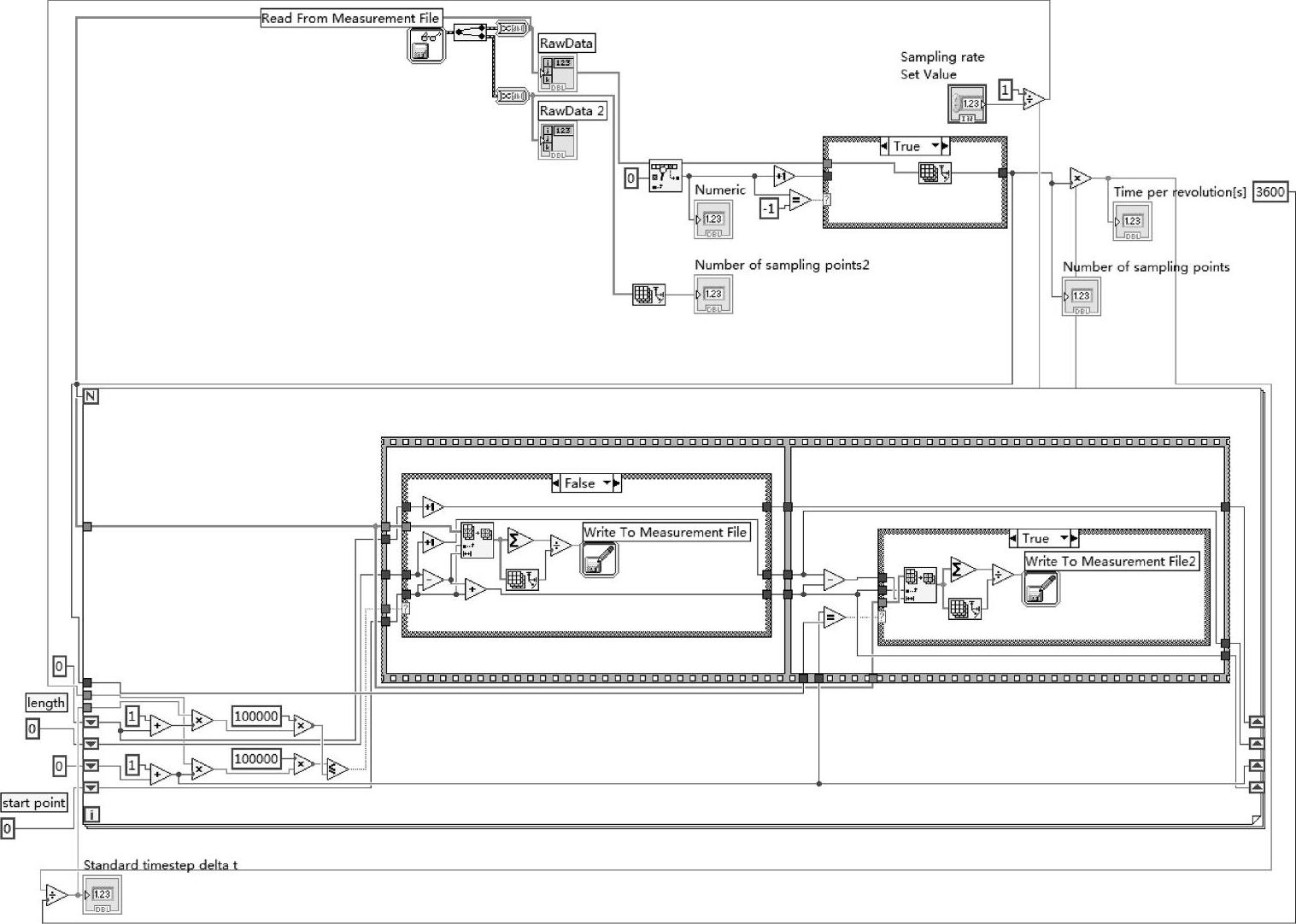
图3-34 相平均处理程序

本书利用巴特沃斯滤波器对测量的叶轮水力激振信号进行低通滤波处理，其截止频率分别为50Hz、100Hz和500Hz，振动位移轨迹如图3-35所示。从图中可以看出，当截止频率为500Hz时，试验获得的振动位移轨迹比较杂乱，说明叶轮振动还与离心泵内其他高频周期性流动现象有关，从图中可以看出，这些流动对振动的影响表现为较高频率和小幅值的波动。由于本书研究的主要针对动静干涉作用下叶轮的振动位移，因此需要采用较低的滤波频率。由于试验用单叶片模型离心泵的叶片通过频率为24Hz，根据奈奎斯特采样定律，如果需要使用离散信号准确获得某频率f_m的原始连续信号主要波形特征，则采样频率f_s必须高于特征信号频率f_m的2倍，即(www.daowen.com)

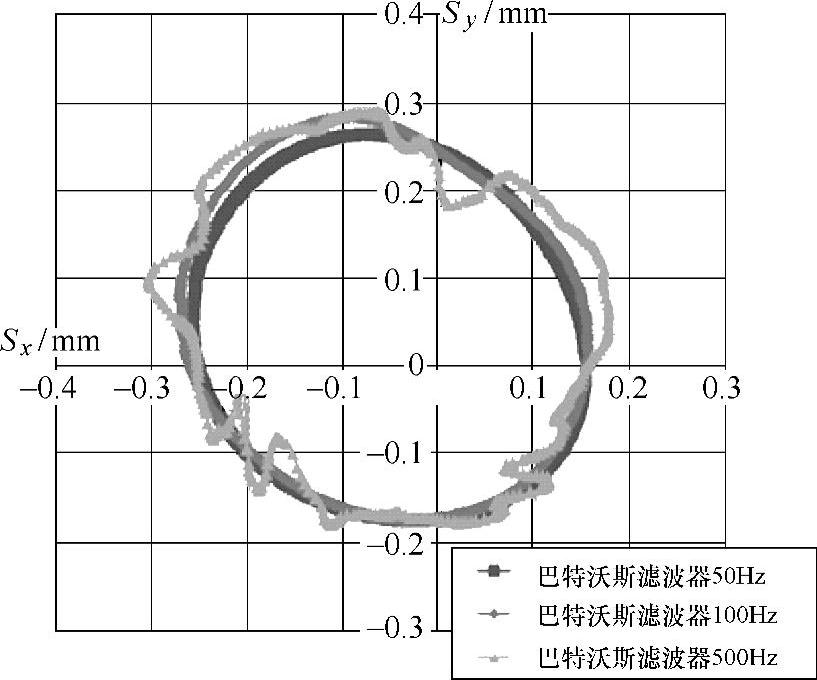
图3-35 不同截止频率下的振动位移信号滤波结果对比

f_s≥2f_m （3-5）

本试验对采样结果进行了50Hz和100Hz的低频滤波。从图3-35中可以看出，这两种截止频率的结果差别不大，呈现较为明显的平滑椭圆分布特征，说明已经基本滤掉了其他不稳定流动作用激励下的振动分量，但50 Hz滤波后得到的轨迹曲线更为平滑，因此选择了50Hz低通滤波频率对试验研究的各工况结果进行滤波处理。

如图3-36所示是“干”测量条件下叶轮在超低转速（80r/min）和额定转速（1440r/min）下x方向典型振动分量的测量结果对比。图中N代表测量过程中各数据采样点的编号，其随着时间的推移，从0，1，2，3…开始逐渐增大，直至最大编号值N_T为止；纵坐标代表测量系统的电压输出值。从图3-36中可以看出，尽管两条曲线代表的测试转速差别巨大，但在“干”测试中，两曲线趋势相同，且差别不大。如果转子质量不平衡，叶轮随着转速的变化在“干”条件下的振动应发生明显变化，即随转速的增大，振动应明显增大。因此，本试验中使用的单叶片叶轮尽管从叶片结构上来看质量分布不对称，但经过动平衡及质量补偿处理后，已经基本达到了转子的质量平衡。曲线的波动主要应是叶轮口环表面不平整等一些加工误差造成的。

图3-36 “干”测量条件下叶轮在80r/min和1440r/min转速下x方向典型振动分量的测量结果对比