目前，由于对流体-结构系统的广义变分原理及有限元求解格式的理论还不成熟，因此，在同一个耦合坐标系统内的直接耦合方法仍不能处理复杂实际工程的流固耦合问题。由于离心泵耦合系统具有模型复杂、结构变形小和流动湍流性强等特点，本书选择已经在很多工程流固耦合问题上得到成功应用的迭代式耦合求解策略。在该策略中，流体域和结构域分别在各自坐标系下进行单独求解，通过耦合界面进行双向的数据传递，可以实现离心泵湍流激振流固耦合系统的求解。这种方法可以实现高效、准确的流固耦合求解，并且可以结合离心泵在CFD和FEM领域研究取得的成果做进一步耦合分析。除此之外，该求解策略的优点还包括：

1）可以发挥不同程序对不同求解域的建模能力，并将其整合进一个程序结构。

2）将耦合系统的问题分成不同的系统进行分别求解，将求解的问题简化，降低了求解系统对计算资源的需求。

3）求解过程中可以获得较好的系数矩阵，获得较好的计算收敛性。

4）可以使用先进的并行计算策略，提高运算效率。

与直接求解方法相比，其缺点主要表现在计算稳定性和误差方面。(www.daowen.com)

迭代式耦合求解策略包括强耦合求解策略（Strongly Coupled Strate-gy）和弱耦合求解策略（Weakly Coupled Strategy），即分别对应双向耦合（Two-way Coupling）求解策略和单向耦合（One-way Coupling）求解策略^[148]，如图2-2和图2-3所示。双向耦合方法主要是针对具有强物理耦合效应的问题，即除了考虑流动对结构的影响，结构的变形或运动对流动的反作用也需要考虑。在这个情况下，结构计算对流动求解的反馈十分重要，是耦合问题得到合理解的前提条件。此外，双向耦合计算可以达到二阶时间精度，因而计算过程更加稳定，能够保证耦合系统能量的守恒。单向耦合方法用于求解结构受流动影响，而结构的反馈对流动的影响不大的情况。单向耦合计算快速，节省计算资源，同时不需要对流体网格进行更新，保证了网格的质量稳定。这种方法主要用于处理流体与结构间的弱耦合效应或结构的变形只影响流体域的边界范围的问题。

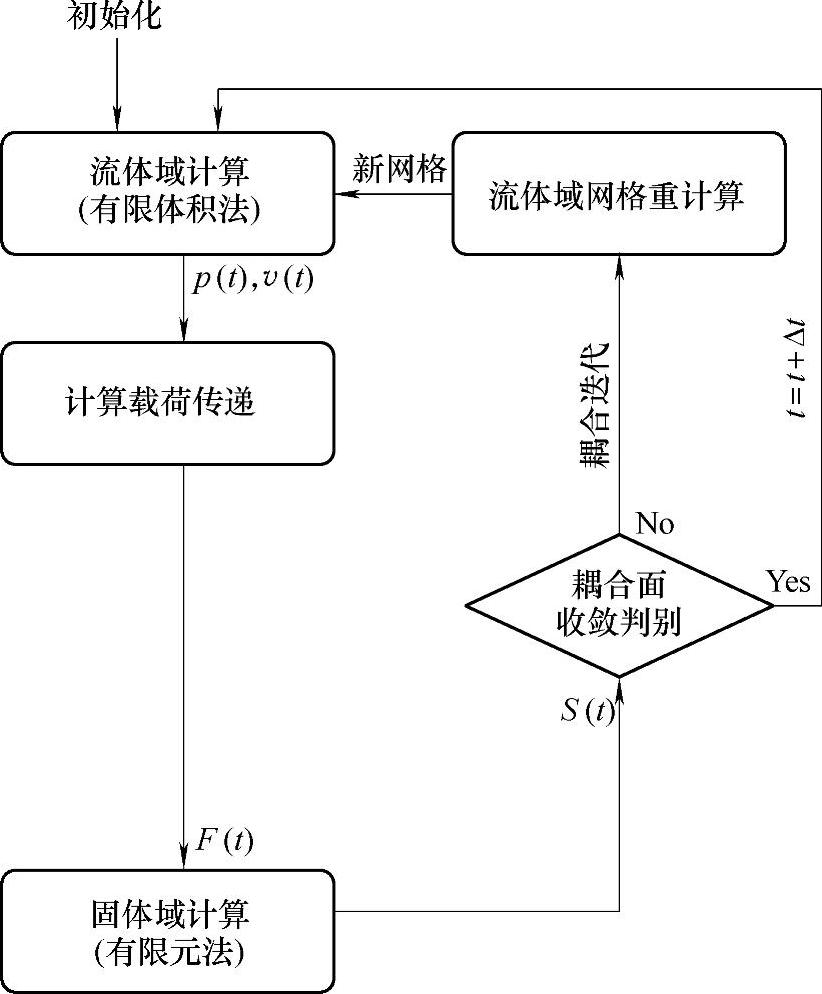
图2-2 双向耦合求解策略

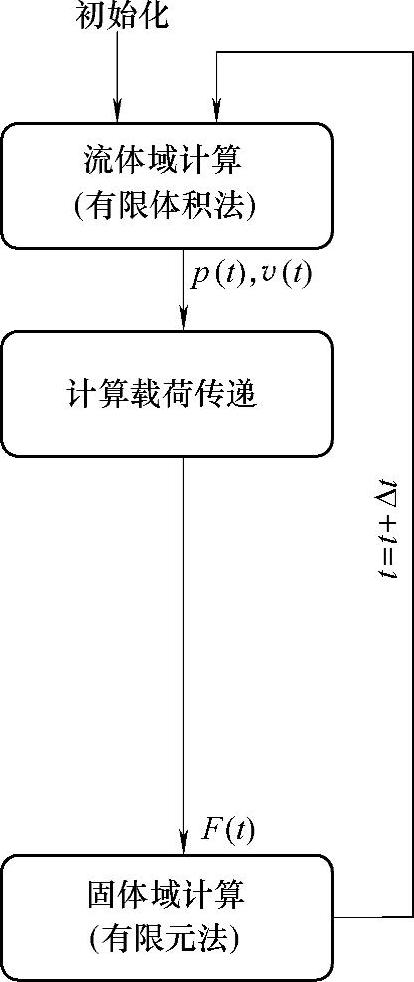
图2-3 单向耦合求解策略