对于流固耦合问题的求解，最大困难在于采用统一坐标系及两相界面的协调问题。众所周知，固体力学中习惯采用Lagrange坐标系，着眼于质点；而流体动力学中更多地使用Euler坐标系，着眼于空间点。单独地应用它们求解流固耦合问题均存在很大的困难。因此，ALE方法被提出并应用。ALE坐标系可以以任意速度在空间运动。若其速度为零，即为Euler坐标系；若其速度等于质点速度，即为Lagrange坐标系。因而，ALE坐标系提供了两种坐标系的一种统一描述，能有效地将固体中常用的Lagrange坐标系与流体中常用的Euler坐标系相联系。由于ALE描述方法在流固耦合问题求解中具有无可比拟的优越性，如今大部分流固耦合问题研究者均采用此方法^[146]。

如图2-1所示是ALE坐标系的定义示意图，图中ξ₁、ξ₂和ξ₃表示初始坐标系的3个坐标轴；x₁、x₂和x₃分别为变换后新坐标系的3个坐标轴。ξ为初始坐标系内的某一向量；x为新坐标系内的一个向量；d为位移向量。

图2-1 ALE坐标系的定义示意图

新坐标系是初始坐标系和其位移的和，表示为：

x=ξ+d（ξ，τ）=x（ξ，τ） （2-14）

t=τ （2-15）式中，τ和t为时间。

通过式（2-14）和式（2-15），移动坐标系（x，t）被转换为新坐标系（ξ，τ），向量d（ξ，τ）用于处理任意移动坐标系。

任意函数f（x，t）=f（ξ+d（ξ，τ），τ）对时间的导数为：

(www.daowen.com)

用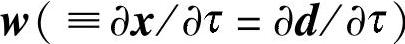代表移动坐标系的速度，就可得到坐标系的转换公式，即：

将式（2-17）应用于Euler坐标系下的N-S方程，就可以得到ALE坐标系中的N-S方程。当遇到移动边界条件问题，例如移动的壁面、变形的结构和自由表面时，ALE方法能够以任意的坐标系统描述流体方程，因此，能够满足物理边界条件的变化^[147]。由此可以推导出ALE坐标系中的不可压流动控制方程为：

连续性方程

▽·u=0 （2-18）

动量方程

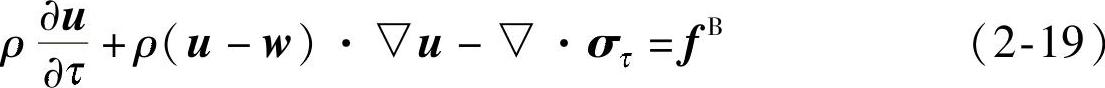
式中，w为坐标系移动速度矢量；u为流体速度矢量；ρ为流体密度；f^B为流体力矢量；σ_τ为应力张量。