本小节考虑样本大小和搜索步长对分数阶傅里叶变换的影响。具体地，当采样频率为1 000 Hz时，研究了样本大小（1 000，2 000，3 000，4 000，50 000）和搜索步长（0. 1，0. 01，0.001，0.000 1）对FRFT 的影响。压力波动信号的FRFT 过程如上所述（6.3.1 节）。同时，使用标准偏差（SD）评估样本大小和搜索步长对FRFT 的影响。SD 的定义见方程式（6.2）。另外，为了研究SD 与平均值之间的关系，还计算了相对标准偏差（RSD）（式6.3）。此外，还使用可以表示结果准确性的相对误差（RE）来讨论绝对误差和平均值之间的关系。相对误差的数学表达见式（6.4）。

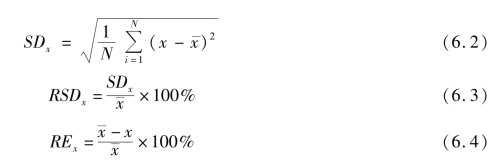
式（6.2）—式（6.4）中，x 表示分数阶傅里叶变换的最佳阶数p 与最大幅值A。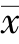表示它们的平均值，N=1，2，3，4，5。

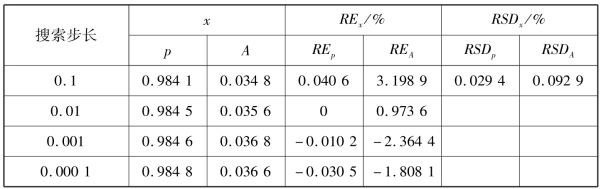
相应的计算结果见表6.2 和表6.3，在表6.2 中，它们的误差均小于1%。当样本大小为4 000时，其误差的绝对值最小。在本书中，影响三维FRFT 峰值的最优阶数p 对于求解不同条件下压力波动信号的特征值至关重要。同时，有一个明显的结论，其误差的绝对值也是最大的。基于最佳阶数p 和信号特征提取的不确定性，所选择的采样大小为4 000。在表6.3 中，所有误差的绝对值不大于1%。通常来讲，搜索步长越小，最佳阶数p 值的精度越高。但是，当搜索步长为0.001 时，FRFT 的幅度A 最大。也就是说，该搜索步长对流体流动信号的特征值的响应最为灵敏。基于该发现，为了深入了解搜索步长对FRFT 的影响，通过MATLAB 中的tic 函数和toc 函数研究了峰值搜索的计算时间，即求得最佳分数阶所消耗的时间。当搜索步长为0. 001 和0. 000 1 时，相应的计算时间分别为9. 172 4 s、9. 764 8 s。不同搜索步长（0.001，0.000 1）下的计算时间差别不大。综上所述，在该研究系统中，所选择的采样大小为4 000，搜索步长设置为0.001。(www.daowen.com)

表6.2　样本大小对FRFT 的影响

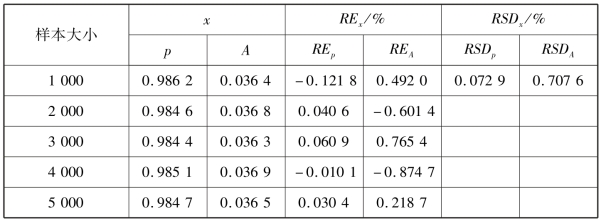
表6.3　搜索步长对FRFT 的影响