分数阶傅里叶变换是一种统一的时频变换，在信号分析和处理中具有独特性和优越性。它在信号检测和重建、滤波和图像处理方面具有广泛的应用。在处理高频信号时，分数阶微分算子可以显著提高其信号强度并改善低频信号。此外，分数阶微分算子的研究可以在文献[276]中找到。在处理实际问题时，定义及其变换机制是不同的。在信号分析中，分数阶傅里叶变换（FRFT）是传统傅里叶变换（FT）的推广，具体将信号的傅里叶变换视为其在频率轴ω上的投影，从而在更宽的频谱上使能量分散，然后可以覆盖信号的所有特征。实际上，信号的FRFT 是在旋转角度α 之后的u 轴上的投影。随着旋转角度在（0，π）范围内的变换，分数阶傅里叶变换可以显示从时域到频域的信号的所有变化特征，这为信号时频分析提供了更多选择。信号的FRFT 和FT 可以用如图6.4 所示进行图解说明。适当的旋转角度可以使信号的能量高度聚集并产生一个窄的积累峰值，这有利于信号的检测和估计。

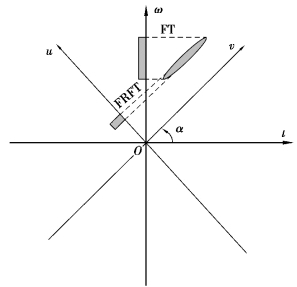
图6.4　时频平面内一组坐标（v，u）相对于原始坐标（t，ω）的旋转角度α(www.daowen.com)

在本节中，我们关注由Ozaktas 等开发的幅度搜索方法。详细的离散化算法可以在文献[150-151]中看到。通常，最佳旋转角度α 不是已知的。在旋转角度优化问题方面，采用步进搜索方法计算信号的FRFT，并在（p，u）平面上形成二维能量分布。在该平面上具有适当阈值的幅度搜索可以实现确定最优变换阶次的目标。在分数阶傅里叶变换的二维平面（p，u）中，采用步进搜索模式找到适当的（p0，u0）并使目标函数式（6.1）最小。该过程可以描述为