三相对称绕组通以对称电流，形成一个按同步转速旋转的合成电枢磁动势即旋转磁场。设i_a，i_b，i_c为三相定子绕组电流的瞬时值，随时间变化。采用单矢量多时轴的方法，取定子绕组A、B、C各相空间轴线为各自的时间轴。定子电流空间综合矢量定义为

综合矢量是一个在空间旋转的矢量，如图15-6所示，各相电流为综合空间矢量在各自相轴上的投影。这种综合矢量的分析方法也适合于电压、磁链等，而且不要求各相物理量必须按正弦变化。

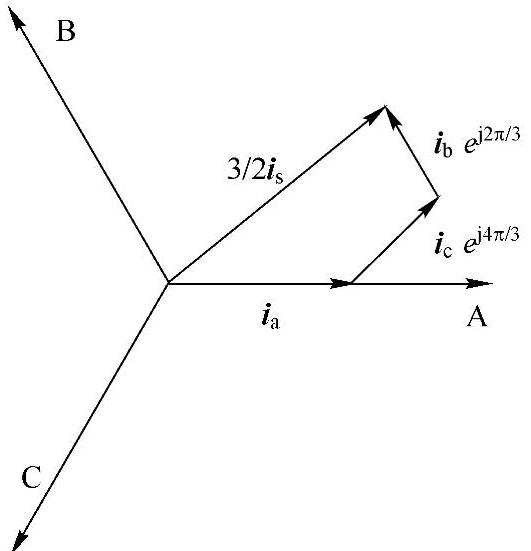
图15-6 定子电流空间综合矢量

旋转空间综合矢量i_s是三相电流的空间矢量和，也同样可以由常用的α-β两相静止坐标系统产生，如图15-7所示。三相A、B、C到两相α-β坐标系统变换（也称为Clarke变换）的关系式为

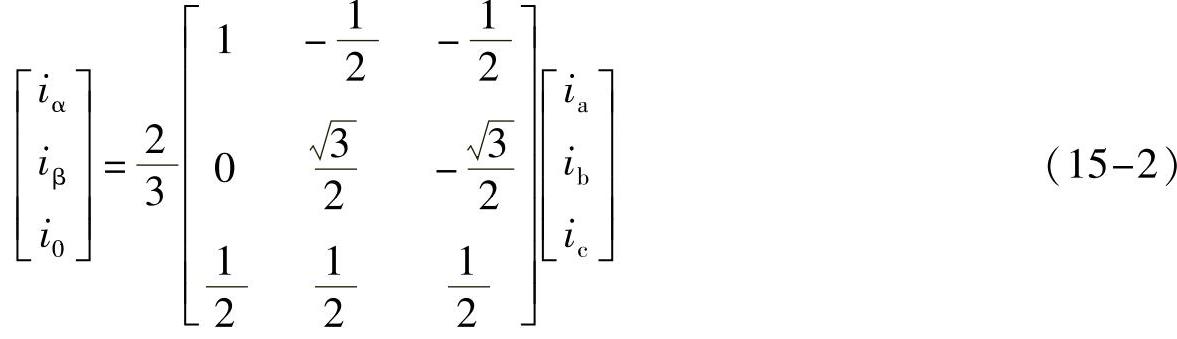
对于三相永磁同步电动机对称接法，通常无相线，三相电流之和为零，即零序电流为零，i₀=0。三个变量只有两个是独立的，即

i_a+i_b+i_c=0

这时坐标变换的公式可以得以简化，三相到两相静止坐标变换即α-β变换的关系式为

i_α=i_a

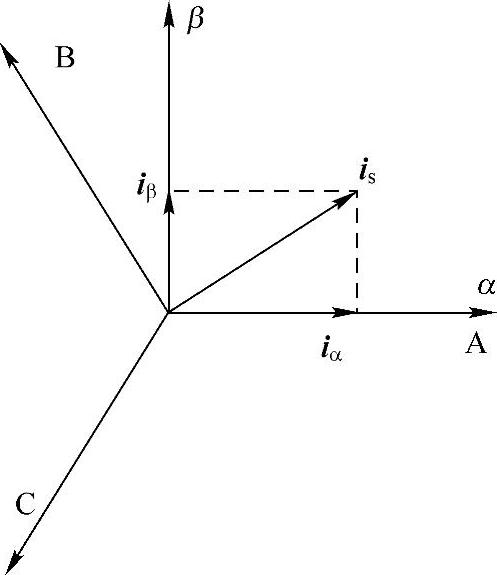
图15-7 A、B、C到α-β的坐标变换

α-β变换后，电磁转矩仍然是转子磁通位置的函数，电磁方程的求解仍很困难，为此进行d-q坐标变换。d-q坐标是建立在转子上的旋转坐标，取转子磁通ψ_f的方向为d轴正方向，如图15-8所示。

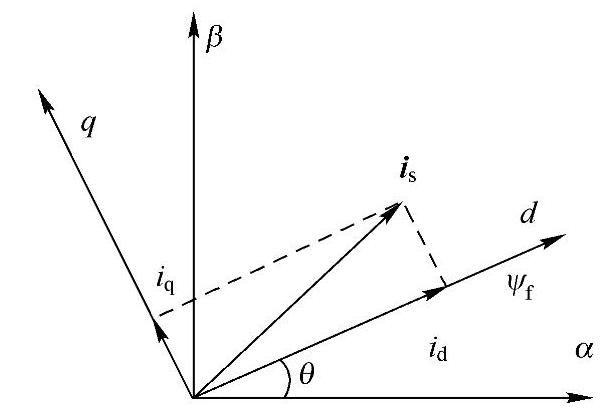
图15—8 α-β到d-q的变换

综合矢量i_s。可分解为沿d-p轴的两个分量i_d，i_q。两相静止坐标变换到转子旋转坐标变换即d-p变换（也称为Park变换）的表达式为(www.daowen.com)

θ为转子d轴领先定子a相（α轴）的电气角度。d-q坐标变换后，定子电压方程可以大为简化，相应的d-q坐标电压方程即Park方程为

R_a为定子相电阻，p=d/dt为微分算子。ω=pθ=dθ/dt为电气角速度。ψ_d，ψ_q为d-q轴磁链，

ψ_f，为转子永磁体磁链，为一常数。L_d、L_q为d-p轴电感。电磁转矩方程为

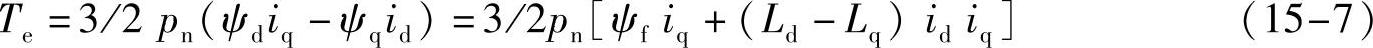
p_n为电动机极对数。

而机械运动方程为

T_e=T_L+JpΩ+BΩ （15-8）

T_L为机械负载转矩，Ω=ω/p_n为机械角速度，J为转动惯量，B为运动阻尼系数。

交轴电流i_q为转矩电流分量，对电磁转矩的产生起主要作用。通常励磁电流分量i_d对电磁转矩的产生贡献不大，且存在使永磁体去磁的可能，故控制i_d=0，即采用磁场定向控制（FOC）方法，使定子磁场与转子磁场始终保持垂直。这时电磁转矩方程和d轴电压方程分别为

T_e=3/2p_nψ_fi_q （15-9）

u_d=-p_nΩL_qi_q （15-10）

电磁转矩与交轴电流i_q成正比，即

T_e=K_ti_q （15-11）

K_t=3/2p_nψ_f为比例常数。这类似于传统它激直流电动机，能够实现电磁转矩的线性化控制。因此，采用i_d=0的矢量控制，可以得到优良的转速控制特性。对于高于额定转速的应用场合，可使i_d＜0，即采用弱磁调速，进行恒功率控制。