上述公式是在把水准面当作水平面、观测视线是直线的条件下导出的，当地面两点间的距离小于300m时是适用的。两点间距离大于300m时就要顾及地球曲率，并加以曲率改正，简称为球差改正。同时，观测视线受大气垂直折光的影响而成为一条向上凸起的弧线，必须加以大气垂直折光差改正，简称为气差改正。以上两项改正合称为球气差改正。

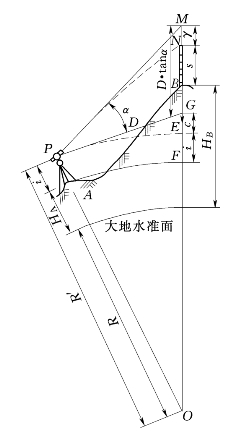
图5-16　球气差对三角高程的影响

如图5-16所示，O为地球中心，R为地球曲率半径（R=6371km），A、B为地面上两点，D为A、B两点间的水平距离，R′为过仪器高P点的水准面曲率半径，PE和AF分别为P点和A点的水准面。实际观测竖直角α时，水平线交于G点，GE就是由于地球曲率而产生的高程误差，即球差，用符号c表示。由于大气折光影响，来自目标N的光沿弧线PN进入望远镜，而望远镜却位于弧线PN的切线PM上，MN即为大气垂直折光带来的高程误差，即气差，用符号γ表示。

由于A、B两点间的水平距离D与曲率半径R′之比很小，例如当D=3km时，其所对圆心角约为2.8′，故可认为PG近似垂直OM，则

MG=Dtanα

于是，A、B二点高差为

令f=c-γ，则公式为

从图5-16可知

(R′+c)2=R′2+D2(www.daowen.com)

即

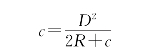
c与R′相比很小，可略去，并且考虑到R′与R相差甚小，故以R代替R′，上式为

根据研究，因为大气垂直折光而产生的视线变曲的曲率半径约为地球曲率半径的7倍，则

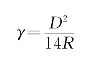
球气差改正为

式中水平距离D以公里为单位。

表5-10给出了1km内不同距离的球气差改正数。三角高程测量一般都采用对向观测，即由A点观测B点，再由B点观测A点，取对向观测所得高差绝对值平均可抵消两差的影响。

表5-10　球气差改正数