小三角测量内业计算包括外业成果的整理、检查、角度、边长和坐标平差计算。一般图根小三角测量计算采用近似平差，一、二级小三角测量用严密平差。下面主要介绍图根三角锁的近似平差计算方法。

1.绘制小三角测量略图

图5-9为单三角锁略图。图中D0或Dn是起始边。从第一个三角形开始，由D0按正弦定律推算与下一个三角形的邻边边长，该边长即为第二个三角形的已知边，这种相邻边称为传距边。依次类推，即可推出所有三角形的边长。为了方便，三角形内角按以下规定编号：已知边所对的角为bi，待求边所对的角为ai，第三边所对的角为ci，称为传距角，亦称为间隔角。

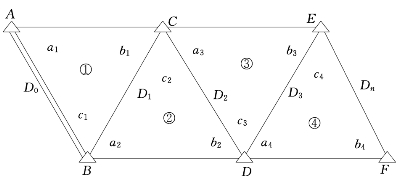
图5-9　单三角锁略图及编号

2.角度闭合差的计算与调整

设为第i个三角形的角度观测值，则各三角形的角度闭合差用式（5-1）计算，图根小三角测量角度闭合差容许值fβ容≤60″。若fi≤fβ容，则进行角度闭合差调整，否则，该三角形的内角要进行外业重测。

设各角度第一次改正数为vai、vbi、vci。因各角度为同精度观测，各改正数应相等。则

改正数取至秒位，第一次改正后的角值为

经过第一次改正后的角度应满足三角形闭合条件，即

3.基线闭合差的计算与调整

根据基线D0和第一次改正后的角值ai、bi，按正弦定理推算另一条基线过程如下。

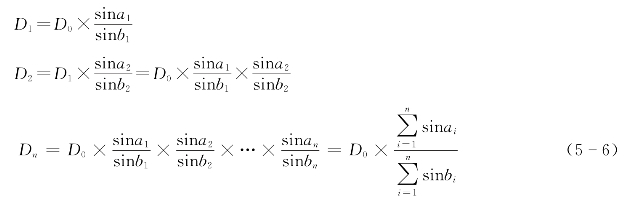
计算的第二条基线应与实测的Dn相等。但由于第一次改正后的角度仍有误差，所以往往≠Dn，从而产生基线闭合差ω′。(www.daowen.com)

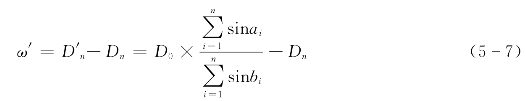
为了消除ω′误差，必须对ai、bi，进行第二次改正，设为角度第二次改正数，则有

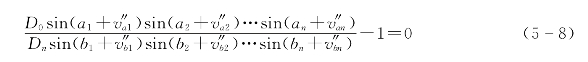
将式（5-8）按泰勒级数展开，取前两项得

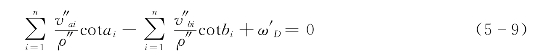
为使第二次改正后仍能满足三角形内角和为180，必使大小相等，符号相反，所以

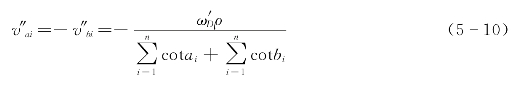
4.边长和坐标计算

根据第二次改正后的角度和基线D0，按正弦定理计算三角形各边长。最后求得的应与Dn相等。求得各边长和改正后的角度，按闭合导线计算各点坐标。

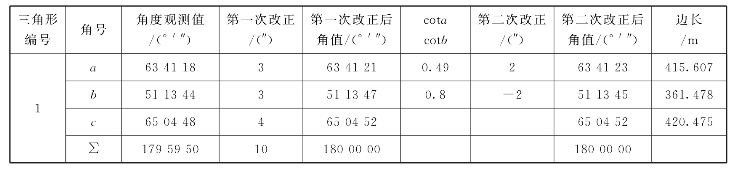
以图5-9为例，按上述推算步骤，角度和边长计算见表5-7，坐标计算见表5-8，表中坐标计算按A-C-E-F-D-B-A闭合导线进行。

表5-7　三角锁闭合差调整与边长计算

续表

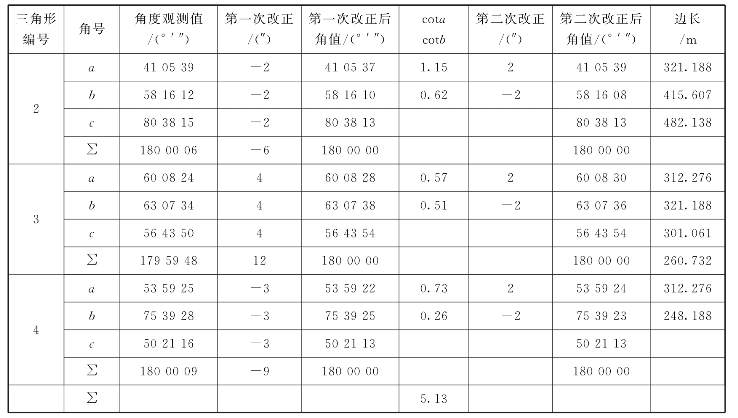
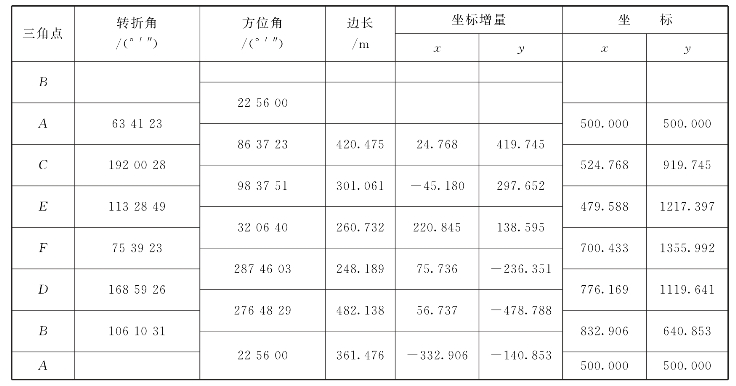
表5-8　三角锁坐标计算