导线内业计算之前，应全面检查导线测量外业工作、记录及成果是否符合精度要求，然后绘制导线略图，标注实测边长、转折角、连接角和起始坐标，以便于导线坐标计算，如图5-5所示。

（一）附合导线计算

由于附合导线是在两个已知点上布设的导线，因此测量成果应满足两个几何条件。

（1）方位角闭合条件：即从已知方位角αAB，通过各βi角推算出终点CD边方位角，应与已知方位角αCD一致。

（2）坐标增量闭合条件：即从B点已知坐标XB、YB，经各边长和方位角推算求得的C点坐标、应与已知C点坐标XC、YC一致。

上述两个条件是附合导线外业观测成检核条件，又是导线坐标计算基础。其计算步骤如下。

1）坐标方位角的计算与角度闭合差的调整。推算CD边坐标方位角为

由于测角存在误差，所以和αAB之间有误差，称为角度闭合差。

本例中=351°36′59″，αCD=351°36′48″，则fβ=+11″，详细数据见表5-5。

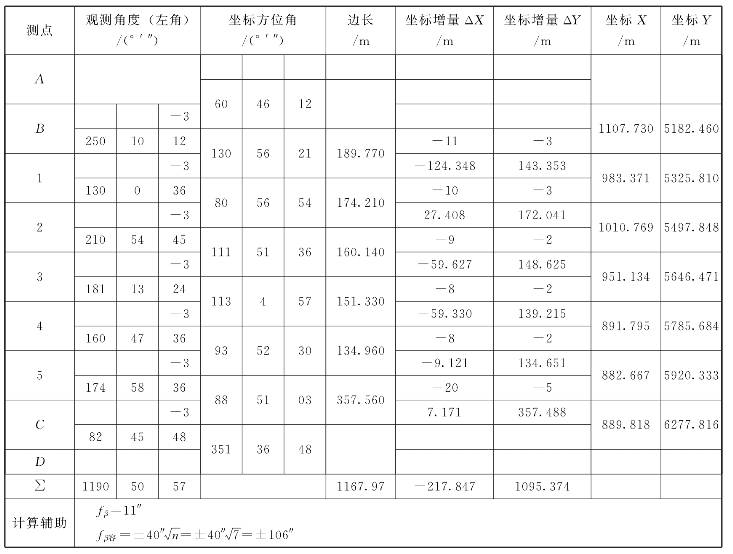
表5-5　附合导线测量计算

图根导线角度闭合差的容许误差为

若fβ≥f容，说明角度测量误差超限，要重新测角；若fβ＜f容，说明角度测量成果合格，可对各角度进行闭合差调整。由于各角度是同精度观测，所以将角度闭合差反符号平均分配给各观测角，然后再计算各边方位角。最后计算的α′CD和αCD，并以是否相等作为检核条件。

2）坐标增量闭合差的计算和调整。利用上述计算的各边坐标方位角和边长，可以计算各边的坐标增量。各边坐标增量之和理论上应与控制点B、C的坐标差一致，若不一致，产生的误差称为坐标增量闭合差fx、fy。计算式为

fx=∑Δx-(xc-xb)

fy=∑Δy-(yc-yb)

由于fx、fy的存在，使计算出的C′点与C点不重合。CC′用f表示，称为导线全长闭合差，用下式表示

fD值和导线全长∑D之比K称为导线全长相对闭合差，即(www.daowen.com)

K值的大小反映了测角和测边的综合精度。不同导线的相对闭合差容许值是不相同的，见表5-2。图根导线K值小于1/2000，困难地区可放宽到1/1000。若K＞K容，应分析原因，必要时重测；一般情况下是量距误差较大。调整的方法是将fx、fy反号按与边长成正比的原则进行分配，对于第i边的坐标增量改正值为

计算完毕，改正后的坐标增量之和应与B、C两点坐标差相等，即∑Δx=ΔxBC，∑Δy=ΔyBC以此作为检核。

根据起始点B的坐标及改正后各边的坐标增量按下式计算各点坐标。

xi+1=xi+Δxi,i+1

yi+1=yi+Δyi,i+1

最后推算出的C′点坐标应与原来C点坐标一致。

（二）闭合导线计算

闭合导线计算方法与附合导线相同，也要满足角度闭合条件和坐标闭合条件。

（1）角度闭合差的计算与调整。闭合导线测的是内角，所以角度闭合条件要满足n边形内角和条件，即

∑β理=（n-2）×180

则角度闭合差为

fβ=∑β测-∑β理=∑β测-（n-2）×180

（2）坐标增量闭合差的计算与调整。闭合导线的起、终点是同一个点，所以坐标增量总和理论值为零，即∑Δx=0，∑Δy=0。则坐标增量闭合差为

角度闭合差fβ，坐标增量闭合差fx、fy及导线全长闭合差f的检验和调整与附合导线计算方法相同。由起点坐标通过各点坐标增量改正计算，求得各点坐标，最后推回到B点坐标并相同，作为计算检核。表5-6为闭合导线计算表。

表5-6　闭合导线测量计算

（三）角度闭合差超限检查方法

在导线测量中，角度闭合差超限要进行外业重测。首先要检查外业记录手簿，看是否有记错、算错的数据，再找外业测量本身的原因。但初学者往往不知道是哪一个角超限或者是否有多个角超限，只得全部重测，这样易造成财力物力及人力的浪费。当只有一个角有较大误差时，可从观测数据中很容易发现是哪一个角超限。检查办法是将前次的推算路线反向之后重新推算各点坐标（注意：只推算，不进行角度闭合差和坐标增量的调整），比较两次坐标计算结果，当发现某一点坐标非常接近时，说明该点的角度测量误差很大。表5-5中，假若3点角度测量误差较大，其余很小，则按A-B-1-2-3-4-5-C-D路线推算结果是1、2、3点坐标准确，4、5点坐标偏离正确值；按D-C-5-4-3-2-1-B-A路线推算结果是5、4、3点坐标准确，2、1点坐标偏离正确值。因此，两次推算结果中，仅3点坐标相近，其余相差较大。若有多个测角误差较大，则仅从数据很难找出原因来。