在角度的观测中，因仪器的对中不严格、观测点上所立标志几何中心偏离目标实际点位、对目标的瞄准不准确及仪器本身读数设备的限度和观测者的估读误差等原因，也会对观测结果产生影响，这种影响称观测误差。观测误差有对中误差、目标偏心误差、瞄准误差和读数误差。

（一）对中误差

对中误差是指仪器在对中时，未严格使仪器中心与测站标志中心重合，从而对在测站上测定目标间的水平角带来影响，也称测站偏心。如图2-18所示，仪器中心为O′，测站标志中心为O，二者的间距设为e，e为对中误差，观测目标点A、B距测站点的距离设为S1、S2，β为正确角值，β′为因未严格对中的实际观测角值，δ1、δ2为因对中偏差引起A、B方向值的误差。

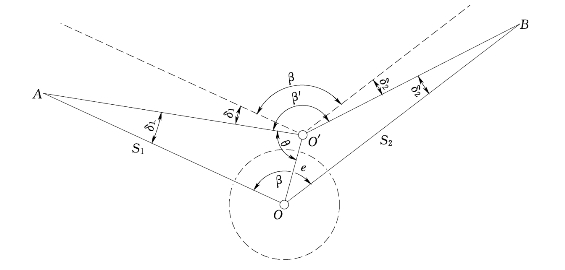
图2-18　对中误差示意图

因δ1和δ2很小，由图易知

又由图知，对中误差e对水平角的影响为

因为，O′可以在以O为圆心，e为半径的圆周上的任意位置，θ角每变化一个dθ，就对应一个dβ，从而可有个影响值。由误差理论可知因仪器的对中误差引起角β的中误差为

将式（2-25）代入式（2-26），得

即

由式（2-27）可知，仪器的对中误差对水平角的影响与下列因素有关：

（1）与目标之间的距离SAB成正比，SAB越大，即水平角越接近180°，此时影响最大。

（2）与测站到目标的距离有关系，距离越短，影响越大。

（3）与对中的偏差e成正比，偏差越大，影响越大。

如果e=3mm，S1=S2=100m，β′=180°，则

而当e=3mm，S1=S2=10m，β′=180°时，则

由此可见，在水平角测量时，应认真精确地对中，对于边长较短的角度或者被观测角接近180°的情况下更应特别注意对中。

（二）目标偏心误差

目标偏心误差是指仪器瞄准在观测的点上所立的标志杆位置同观测点的标志中心不在一铅垂线上或者所立的标志杆不在观测点上，从而因照准目标的偏心对水平角产生的影响。如图2-19所示，A、B分别为观测点标志的实际中心，A′、B′分别为仪器瞄准标志杆上的点在水平面上的垂直投影点，β为正确角值，β′为因目标偏心的实际观测角值，δ1、δ2为因目标偏心引起A、B方向值的误差。

图2-19　目标偏心误差示意图

因δ1和δ2很小，由图易知(www.daowen.com)

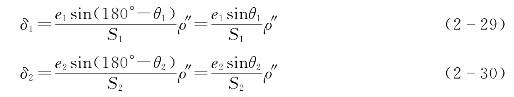
因为，A′可以在以A为圆心，e1为半径的圆周上的任意位置，θ1角每变化一个dθ，就对应一个δ1，从而可有个影响值。由误差理论可知因目标偏心引起A方向的中误差为

将式（2-29）代入上式，得

同理可得

从而由误差传播定律可得因目标偏心对水平角的影响为

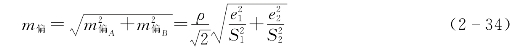
由式（2-29）、式（2-30）及式（2-34）可知，目标偏心的误差给水平角的影响与下列的因素有关：

（1）与测站到目标的距离有关系，距离越短，影响越大；

（2）与目标偏心的方向有关系，若目标偏心在观测方向上，此时对水平角无影响；若标偏心垂直于观测方向，此时对水平角影响最大；

（3）与目标偏心的偏差大小也有关系，偏差越大，影响越大。

如果e1=e2=3mm，S1=S2=100m，则

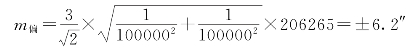
而当e1=e2=3mm，S1=S2=10m时，则

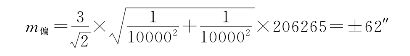
由此可见，在瞄准目标时，应尽量瞄准目标的底部，对于观测边长较短时更应特别注意将标志杆立直，且立于观测点的中心上，并使标志杆尽量细一些。

仪器的对中误差和目标偏心误差，就误差的本身性质而言，二者均是偶然误差，但是仪器安置和目标标志设置一旦完成，则仪器的对中误差和目标偏心误差的真值就不再发生变化，无论水平角的观测采用多少个测回，因这两项误差分别在各测回之间均保持相同，绝不会通过增加水平角观测的测回数而减小仪器的对中误差和目标偏心误差对水平角的影响。所以，在水平角的观测中，一定要注意仪器的对中误差和目标偏心误差的影响，特别是当测站到目标的距离较短时，尤应仔细对中，观测点上的标志杆尽可能细，并立直，且立于观测点的中心上。

（三）瞄准误差

瞄准误差是人眼在通过望远镜瞄准远处目标时所产生的一种偶然误差，它取决于望远镜的照准精度，目标与照准标志的形状、大小及颜色，人眼对照准标志在望远镜中的影像的判别力，目标影像的亮度和清晰度，目标成像的稳定性以及通视情况等因素。一般认为瞄准误差与望远镜的放大率和人眼的分辨率有直接关系，是影响瞄准误差的主要因素。其误差的大小可以表示为

其中ν为望远镜的放大率；p″为在目标影像亮度合适、成像稳定、清晰度好等较为理想的状态下，人眼通过望远镜观测远处目标的瞄准分辨率。在此理想状况下，当以十字丝的双丝来照准目标时，人眼的瞄准分辨率p″=10″，并取ν=25（对DJ6经纬仪而言），则得瞄准误差为

由于影响瞄准误差的因素很多，实际上dβ″一般比上面的计算值大一定的倍数k，即

由实验数据可统计得出：在目标亮度适宜、标志杆宽度较小、成像稳定及远处目标背景清晰等的情况下，k可取1.5～3.0。

（四）读数误差

读数误差主要取决于仪器的读数设备，一般以仪器的最小估读数为读数误差的极限。对于采用分微尺测微器的J6型经纬仪而言，其估读的极限误差为分划值的1/10，即±6″。当然，在读数窗照明不佳、读数显微镜的目镜焦距未调好以及观测者的技术不熟练等情况下，估读的极限误差则会增大，从而读数误差将超过6″。