1.水静压强

水静压强是水处于静止或相对静止时的水压强。

图4-1　流体静压力的方向

水静压强具有两个重要特性。

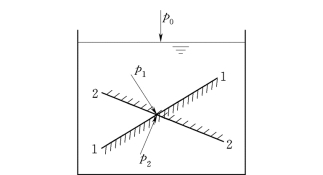
特性一：水静压强的方向总是垂直并指向作用面，如图4-1所示。

特性二：在静止水内部任意点处水静压强的大小与作用面的方位无关，即任一点上各方向的水静压强均相等，如图4-2所示。

2.水静力学基本方程式

图4-3为一开口容器，盛有密度为ρ的水，且所受的质量力只有重力。水静力学基本方程式为

式中 z——水中点距基准面的高度，表示单位重量水所具有的位置势能，又称为位置高度或位置水头，m；

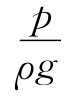——单位重量水的压强势能，又称压强高度或压强水头，m。

(www.daowen.com)

图4-2　流体静压强各向相等示意图

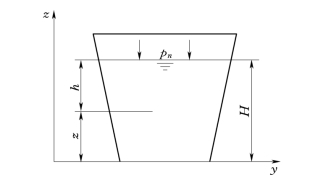
图4-3　流体静力学基本方程导出示意图

位置势能与压强势能之和称为单位重量水的总势能；位置水头与压强水头之和称为测压管水头。式（4-4）说明在静止水中，任何一点的压强势能和位置势能之和是常数，即总静能头保持不变，它是能量守恒定律在水静力学中的具体体现；或者说，绝对静止水中各点的测压管水头都相等。

在工程计算中常需计算有自由水面的绝对静止水中任意一点的静压强。为此，可由水静力学基本方程式（4-4）得到它的计算公式。

如图4-3所示，在自由表面z＝z 0处，设压强p＝p 0，将此边界条件代入式（4-4）中，可得积分常数为

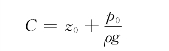
再将积分常数代入式（4-4）可得

式（4-5）是计算有自由水面的绝对静止水中任意一点的静压力公式，它也是水静力学基本方程的又一表达式，式中h为点距自由水面的深度。从式（4-5）可看出：

（1）在静止的水中，静压强随深度按直线规律变化。

（2）在静止的水中，位于同一深度的各点的静压强相等，即任一水平面都是等压面（对于海洋，等压面为近似球面的曲面）。

（3）在静止水中，任一点的静压强由两部分组成：一部分是自由水面上的压强，另一部分是该点到自由水面的单位截面积的水柱重力ρgh。