物体各部分之间不发生相对位移时,依靠分子、原子及自由电子等微观粒子的热运动而产生的热量传递称为热传导,简称导热。
(一)温度场
温度场是指某一时刻,物体内部各点温度分布的总称。一般来说,它是空间坐标和时间坐标的函数。即
![]()
若温度场不随时间变化,称为稳态温度场,即
![]()
若温度场只沿空间一个方向变化,则称为一维稳态温度场,即
![]()
例如,火电厂中锅炉、汽轮机的启停和变工况条件下运行,汽包壁、汽缸壁的温度场均为非稳态温度场,而在稳定工况下运行时,其温度场为稳态温度场。本书仅讨论一维稳态温度场。
为了形象地表示物体内的温度场,常使用等温面(线)来表示。等温面是由物体内温度相同的点组成。在任何一个二维的截面上等温面表现为等温线。不同温度的等温线不相交。在等温面上或等温线上不存在温差,等温线上温度相等,所以沿着等温线无热量传递。但不同的等温面(线)间存在温差,从而有热量从高温处向低温处传递。等温面法线方向上单位长度的温度变化率称为温度梯度,记为Ф,单位为W(瓦)或k W(千瓦)。傅里叶定律给出了热流量与温度梯度之间的关系式。
(二)导热基本定律——傅里叶定律
傅里叶在实验研究的基础上得出,单位时间内通过单位面积所传递的热量正比例于垂直于截面方向的温度梯度,即
![]()
式中 Ф——单位时间内通过某一给定面积的热量为热流量,W;
q——单位时间内通过单位面积的热量称为热流密度,W/m2;
λ——比例系数,又称导热系数,W/(m·℃)。
从上面分析可以看到,要计算导热的热流密度,首先要知道公式中的比例系数即导热系数。
从导热基本定律公式得出
![]()
在数值上,它等于在单位温度梯度作用下物体内所产生的热流密度。导热系数是表示物质导热能力强弱的物理量,导热系数越大,表明物质的导热能力越强。导热系数的数值取决于物质的种类和温度等因素。气体的导热系数在物质三态中是最小的,其范围在0.008~0.2W/(m·℃)之间,例如干空气的导热系数为0.0259W/(m·℃)。液体的导热系数较气体的导热系数大,其数值范围为0.1~0.7W/(m·℃)。如20℃时水的导热系数为0.599W/(m·℃)。金属的导热系数很高,其数值范围为22~458W/(m·℃)。如20℃时铜的导热系数为399W/(m·℃);碳钢(含碳量w C≈1.5%)为36.7W/(m·℃)。
习惯上把导热系数小的材料称为保温材料(又称隔热材料或绝热材料)。我国国家标准规定,凡平均温度不高于350℃时导热系数不大于0.12W/(m·℃)的材料称为保温材料。工程上,常用保温材料来减少设备和管道的散热,如矿渣棉、岩棉、膨胀珍珠岩、微孔硅酸盐、中空微珠和泡沫塑料等。
(三)一维稳态导热
1.平壁的导热
工程上常用的平壁是指壁的长、宽尺寸比其厚度大得多的平壁,称为无限大平壁,这样的平壁导热可简化为只沿厚度方向进行的一维稳态导热。图1-25为单层平壁导热示意图。平壁两侧表面分别维持均匀而恒定的温度tW 1和tW 2,且tW 1>tW 2,壁的厚度为δ,导热系数λ是常数。
无内热源的一维稳态导热微分方程为
![]()
边界条件:
![]()
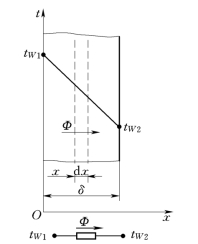
图1-25 单层平壁导热
![]()
积分式(1-33),得其通式为
![]()
式中 c1、c2——积分常数,由边界条件确定。最后解得温度分布为
![]() (https://www.daowen.com)
(https://www.daowen.com)
式(1-35)表明常物性无内热源平壁内温度分布沿x方向线性变化。根据傅里叶定律可得通过平壁的热流密度为
![]()
式(1-36)可改写成

式中 rd——单位导热面积的导热热阻,m2·K/W。
由此可知,热流密度与温压成正比,与热阻成反比。
若平壁的导热面积为A,则所传递的热流量为

式中 Rd——导热面积为A时的导热热阻,K/W。
工程上经常遇到多层平壁的导热问题,例如锅炉炉墙(由耐火材料层、保温材料层和外加钢质护板组成)、外包保温层的汽轮机外壳等均可看作多层平壁的实例。图1-26是由三层平壁组成的多层平壁,各层的厚度分别为δ1、δ2、δ3;导热系数分别为λ1、λ2、λ3;两侧温度均匀恒定,并分别为tW 1和tW 4。层间接触良好,相邻两层分界面上的温度均匀。
应用热阻串联原理,并借助于电路欧姆定律,可以很方便地写出三层平壁导热的热流量计算式,即
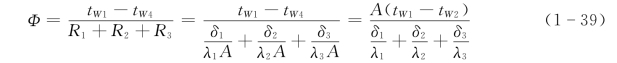
2.圆筒壁的导热
由于圆形管道和圆筒形容器不但具有较高的强度,而且制造方便,受力均匀,节省金属材料,所以发电厂的汽水管道多用圆形,如锅炉的汽包、水冷壁管、过热器管以及汽轮机凝汽器的冷却水管等。
图1-27为一常物性、无内热源的单层圆筒壁,内外半径分别为r1和r2;内外表面的温度恒定、均匀,并分别维持tW 1和tW 2;长度l远大于外径d 2。
若选用圆柱坐标,上述圆筒壁的导热微分方程为
![]()
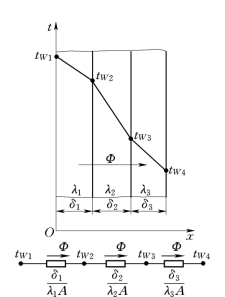
图1-26 多层平壁导热
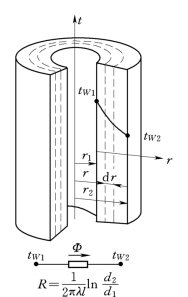
图1-27 单层圆筒壁导热
边界条件为:
![]()
积分式(1-40),得其通式为
![]()
式中 c1、c2——积分常数,由边界条件求得。最后解得圆筒壁中的温度分布为
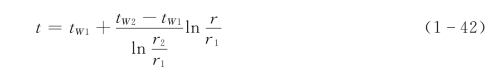
由式(1-42)可知圆筒壁温度分布呈对数曲线。
根据傅里叶定律,通过长度为l的圆筒壁的导热量为
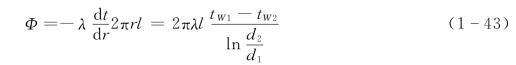
或

与分析多层平壁的导热一样,对于多层圆筒壁导热也可方便地利用热阻叠加的原则,得到如图1-28所示三层圆筒壁的导热量计算式,即
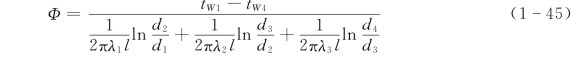
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。







