（一）热力学第一定律的实质

热力学第一定律是能量守恒与转换定律在热现象中的应用。在工程热力学中，热力学第一定律可表述为：热能可以转换为功，功也可以转换为热能，一定量的热能消失时，必产生一定量的功，消耗一定量的功时必出现与之对应的一定量的热。

热力学第一定律也可表述为：第一类永动机是不可能制造成功的。

（二）热力学能和总能

热力学能是指组成热力系统的大量微观粒子本身所具有的能量，它包括内动能、内位能及维持一定分子结构的化学能和原子核内部的原子能等。在无化学反应及原子核反应的过程中，化学能、原子核能都不变化，可以不考虑，因此热力学能的变化只是内动能和内位能的变化。由于热运动而具有的内动能是温度的函数；由于分子间相互的作用力而具有的内位能决定于气体的比体积和温度。因此，热力学能是状态参数，即u＝f（T，v）。

我国法定计量单位中热力学能的单位是焦耳，用符号J表示。热力学能用U表示，单位质量工质所具有的热力学能称为比热力学能，用u表示，单位为J/kg。

除热力学能外，热力系统还由于其宏观运动速度而具有的宏观动能Ek以及其在重力场中所处的位置而具有的宏观势能E p。因此，热力系统的总能量为

式中 m——热力系统中工质的质量，kg；

c f——热力系统相对于某外部坐标系具有的宏观速度，m/s；

z——热力系统相对于某外部坐标系具有的高度，m。对于单位质量工质而言

（三）焓

在有关热工计算中时常有U＋p V出现，为了简化公式和简化计算，把它定义为焓，用符号H表示，即

单位质量工质的焓称为比焓，用h表示，即

（四）推动功

因工质在开口系统中流动而传递的功称为推动功。如图1-3所示，质量为m的工质，在压力p 1的作用下，位移l进入系统，则推动功为

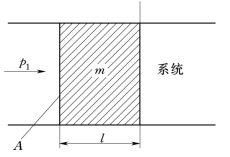
图1-3　推动功示意图

式中 A——截面积。

所以

若1kg工质进入系统，则外界所做的推动功为

同理，当系统出口处工质状态为（p 2，v 2）时，1kg工质流出系统，系统所做的推动功为p 2 v 2。

（五）闭口系统的能量方程

闭口系统的能量方程根据能量守恒原则，外界能量的减少量应该等于热力系能量的增加。单就热力系统而言，其表达式为

对于闭口系统，进入和离开系统的能量只包括热量和做功两项。

如图1-4所示，取气缸活塞系统中的工质为系统。设系统开始时处于平衡态1，过程中系统吸热Q，对外膨胀做功W，最后到达平衡态2。若工质的宏观动能和位能的变化可忽略不计，则工质（系统）储存能的增加即为热力学能的增加ΔU。根据式（1-12）可得

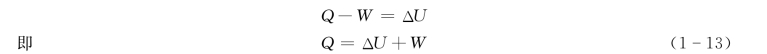
式（1-13）是热力学第一定律应用于闭口系统的能量方程式，是最基本的能量方程式，称为热力学第一定律的解析式。它对闭口系统各种过程（可逆过程或不可逆过程）各种工质都适用。

对于微元过程：

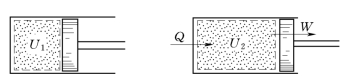
图1-4　闭口系统能量平衡

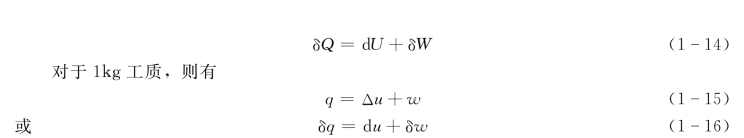
（六）稳定流动系统的能量方程

若流动过程中，开口系统内部及其边界上各点工质的热力参数都不随时间而变，这种流动过程称为稳定流动过程。

图1-5是一稳定流动系统，假想截面1-1和截面2-2之间的空间为研究对象，工质不断地从截面1-1流进系统，从截面2-2流出系统。外界不断地供给系统热量，系统同时对外输出轴功。

假定单位时间内有1kg工质从截面1-1进入系统，其参数为压力p 1、比容v 1、温度T 1、热力学能u 1、速度c f1，进口截面1-1的中心距基准面的高度为z 1，根据稳定流动的概念，在同样的时间内也有1kg工质从截面2-2流出系统，其参数为压力p 2、比容v 2、温度T 2、热力学能u 2、速度c f2，出口截面2-2的中心距基准面的高度为z 2。

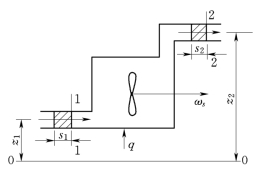
图1-5　稳定流动系统示意图

在单位时间内经过截面1-1的工质带入系统的能量有：

（1）工质的热力学能u 1，J/kg。

（2）工质的宏观动能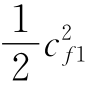，J/kg。

（3）工质的重力位能gz1，J/kg。

（4）外界对系统做的流动功p 1 v 1，J/kg。

同理，1kg工质流出系统时，带走的能量有：

（1）工质的热力学能u 2，J/kg。(www.daowen.com)

（2）工质的宏观动能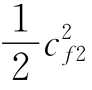，J/kg。

（3）工质的重力位能gz2，J/kg。

（4）外界对系统做的流动功p 2 v 2，J/kg。

此外，在单位时间内，外界向系统加入了热量q，系统向外界输出轴功ws。

根据稳定流动的条件，可以列出能量平衡方程式：

整理后，得

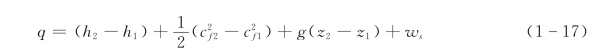
对于m kg工质

对于微元过程

式（1-17）称为稳定流动系统的能量方程，它适用于理想气体和实际气体，也适用于可逆过程和不可逆过程。

若将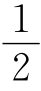mΔc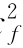、mgΔz和W s三项之和称为技术功（技术上可资利用的功），用W t表示，即

将式（1-21）代入式（1-17），稳定流动系统的能量方程也可写成

对于单位质量工质

对于微元过程

（七）稳定流动系统能量方程的应用

1.动力机械

利用工质膨胀而获得机械功的热力设备，称为动力机械，如汽轮机等。

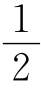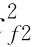图1-6是动力机械的示意图。工质流经动力机械时，工质膨胀，压力降低，对外做轴功。由于工质进、出口速度相差不大，可认为（c－c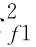）≈0；进、出口高度相差很小，可认为g（z2－z1）≈0；又因工质流经动力机械所需的时间很短，可认为是绝热过程。因此，稳定流动能量方程简化为

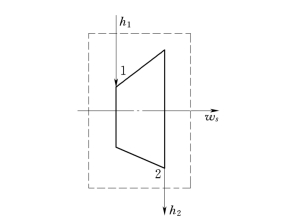
图1-6　动力机械示意图

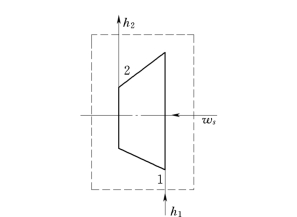
图1-7　压缩机械示意图

2.压缩机械

如图1-7所示，当工质流经泵、风机、压气机等一类压缩机械时，受到压缩，压力升高，外界对工质做功，情况与上述动力机械正好相反。稳定流动能量方程可简化为

如果压气机的散热量不能忽略，则

3.喷管

喷管是一种特殊的管道，工质流经喷管后，压力下降，速度增加，热能转化为动能，不对外做轴功。图1-8是喷管的示意图。稳定流动系统能量方程可简化为

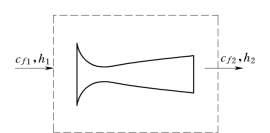
图1-8　喷管示意图

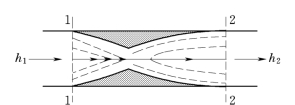
图1-9　节流示意图

4.绝热节流

工质在管内流过缩口或狭缝时，会遇到阻力，使工质的压力降低，形成旋涡，这种现象称为节流，如图1-9所示。工质流经缩口可看作绝热，对外不做功，位能差、动能差通常可忽略不计。因此，稳定流动系统能量方程可简化为

5.热交换器

热力工程中常见的锅炉、加热器和冷却器等均属于热交换器。图1-10是表面式热交换器的示意图。稳定流动能量方程可简化为

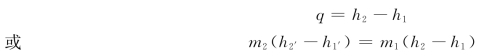
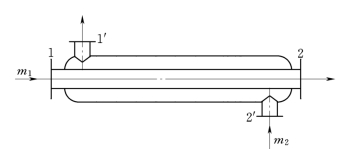
图1-10　换热器示意图

图1-11　摩擦耗散