铸造CAE对铸造过程中的物理、冶金现象进行分析，配合精确的边界条件，分别求解方程。其基本数学方程及变量关系见表7-1。充型凝固过程可以用连续性方程（质量守恒定律）、动量方程（动量守恒定律）以及能量方程（能量守恒定律）描述。

表7-1 铸造过程中的物理现象、基本数学方程及变量关系

（续）

假设金属液为不可压缩流体，没有受到除重力以外的体积力及表面力，几个基本方程分别为

连续性方程

纳维-斯托克斯方程

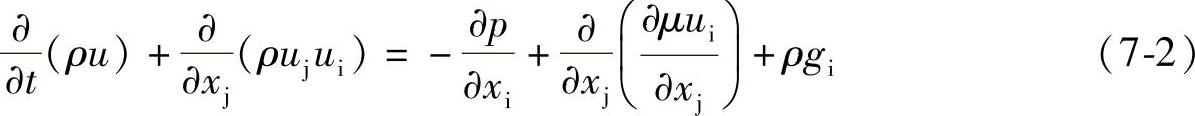
能量方程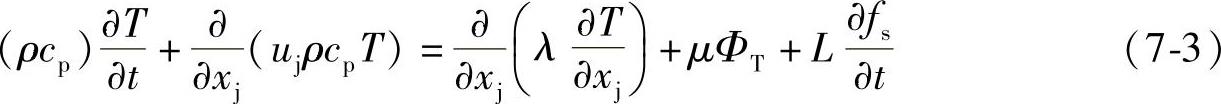

式中 u_i、u_j——速度分量；

x_j——直角坐标系中的x，y，z；(www.daowen.com)

ρ——金属液密度；

t——时间；

μ——金属液动力粘度；

p——金属液压力；

g_i——重力加速度；

c_p——比热容；

T——温度；

λ——热导率；

Φ_T——耗散函数；

L——相变潜热；

f_s——固相分数。

上述方程只是基本方程，还假定了很多前提条件。由于充型凝固过程不仅涉及金属液流动问题，还涉及流动过程自由表面确定，以及热量传导和金属液凝固相变等现象，其过程非常复杂，铸造模拟所涉及的方程还不止这些。求解这些复杂的方程组，加上压铸件往往形状复杂，所以欲精确求解上述偏微分方程组的解析解是不可能完成的任务。目前，铸造过程模拟软件大多使用数值计算方法，数值计算方法实际上是一种近似解法。数值计算是基于对计算域的离散，不同数值方法对计算域的离散方法不同，对边界的处理方法也不同，计算效率和计算精度往往也不同。