【工程实例1】江垭水利枢纽

江垭水利枢纽工程（图3.112）位于湖南省张家界市境内的澧水支流娄水中游，大坝坝址在慈利县江垭镇上游1.5km处。江垭水利枢纽工程坝址控制流域面积为3711km2，水库总库容为18.34亿m3，其中防洪库容为7.40亿m3，最大泄洪能力为17000m3/s。右岸地下厂房电站装机300MW，多年平均年发电量为7.56亿kW·h。该工程以防洪为主，兼有发电、灌溉、航运、供水、旅游等综合效益。工程由大坝、通航建筑物、发电系统和灌溉取水系统等构成。大坝为全断面碾压混凝土重力坝，坝高131m。

【问题】重力坝坝踵和坝址应力计算。

图3.112　江垭水利枢纽

图3.113　重力坝应力计算简图

分析：沿坝轴线取单位长度进行计算（图3.113），梁受到的荷载有重力、水荷载、风浪荷载、渗透压力等的作用，所有荷载均可以沿竖直方向和水平方向进行分解，把重力坝看成是固接于地基的悬臂梁进行计算，实际上就是求压缩和弯曲的组合变形，水平截面上的正应力计算可以采用偏心受压公式计算。

假定水平截面上正应力σy按直线分布，可根据偏心受压公式计算上、下游边缘应力σyu和σyd：

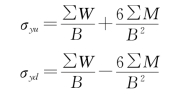
式中：∑W为作用于计算截面以上全部荷载的铅直分力的总和，kN；∑M为作用于计算截面以上全部荷载对截面垂直水流流向形心轴的力矩总和，kN·m；B为计算截面的长度，m。

根据江垭大坝典型剖面（图3.114），计算建基面水平截面上竖直方向的正应力（不计渗流和浪压力的影响）。混凝土的容重γ=24.0kN/m3，水的容重γw=9.81kN/m3。

图3.114　挡水坝典型剖面（单位：m）

解：

计算水压力和自重，计算过程如下：

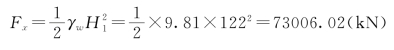
W1=12×131×24=37728（kN）

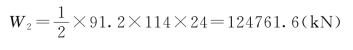
W=W1+W2=37728+124761.6=162489.6（kN）

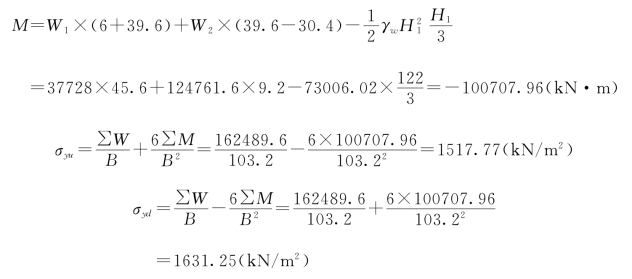
坝基面竖直方向正应力分布如图3.115所示。

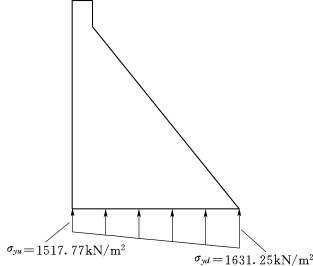
图3.115　坝基面竖直方向正应力分布

【工程实例2】温州市龙湾区蓝田水闸工程

蓝田水闸（图3.116）是温州城市东片防洪排涝重点工程，也是龙湾区防洪工程的控制性工程。水闸挡潮设计标准为100年一遇，排涝能力为50年一遇，闸孔为3孔×6m，净宽18m，设计流量为280m3/s，灌溉农田15多万亩，工程等级为Ⅱ等中型水闸。

图3.116　蓝田水闸工程

【问题】水闸闸室基底应力计算。

分析：闸室基底应力的大小及其分布状况，一般与闸室结构的布置型式，作用荷载的大小、方向和作用点，闸底板的形状尺寸和埋置深度以及地基土质等因素有关。闸室基底应力目前普遍采用材料力学偏心受压公式计算，考虑到闸墩和底板在顺水流方向的刚度很大，闸室基底应力可近似地认为呈直线分布（图3.117）。

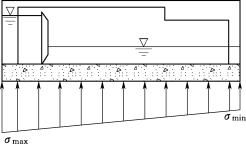
图3.117　闸室基底应力分布

解：

（1）对于结构布置和受力情况均对称的闸段（相邻两沉降缝之间的闸段），基底压力按偏心受压公式计算：

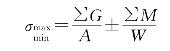
式中：为闸室基底压力的最大值或最小值，kPa；∑G为作用在闸室上的全部竖向荷载（包括闸室基础底面上的扬压力在内），kN；∑M为作用在闸室上的全部竖向和水平向荷载对于基础底面垂直水流方向的形心轴的力矩，kN·m；A为闸室基础底面的面积，m2；W为闸室基础底面对于底面垂直水流方向的形心轴的截面矩，m3。

或

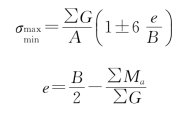
式中：为闸室基底压力的最大值和最小值，kPa；e为偏心距，m；∑G为作用在闸室上的全部竖向荷载，kN；∑Ma为作用在闸室上的竖向和水平荷载对闸底板底面上游角点a处的力矩和，逆时针旋转为正，顺时针旋转为负，kN·m；A为闸室基础底面的面积，m2；B为闸室底板的宽度，m。

（2）对于在垂直水流方向的结构布置及受力情况不对称的闸孔，如多孔水闸的边闸孔或左右不对称的单闸孔，闸室基底应力按双向偏心受压公式计算，即

式中：∑Mx、∑My分别为作用在闸室上的全部竖向和水平向荷载对于基础底面形心轴x、y的力矩，kN·m；Wx、Wy分别为闸室基础底面对于该底面形心轴x、y截面矩，m3。或

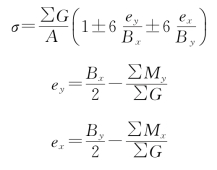
式中：σ为闸室底板角点基底压力，kPa；ex为合力对x轴的偏心距，m；ey为合力对y轴的偏心距，m；Bx为底板x方向的宽度，底板顺水流方向宽度；By为底板y方向的宽度，底板垂直流方向宽度；∑G为作用在闸室上的全部竖向荷载，kN；∑Mx为作用在闸室上的竖向和水平荷载对闸底板底面上x轴的力矩和，逆时针旋转为正，顺时针旋转为负，kN·m；∑My为作用在闸室上的竖向和水平荷载对闸底板底面上y轴的力矩和，逆时针旋转为正，顺时针旋转为负，kN·m；A为闸室基础底面的面积，m2。

【例题】某拦河闸为开敞式水闸，取水闸中间的一个独立的闸室单元进行分析，闸室结构布置见图3.118，已知闸室宽度B=14.0m，闸室面积A=14×9=126m2，各种工况下荷载计算结果见表3.6～表3.8。求各工况下闸室底板的应力。

（1）完建期。完建期的荷载（图3.119）主要包括底板重力G1、闸墩重力G2、闸门重力G3、工作桥及启闭机设备重力G4、公路桥重力G5和检修便桥重力G6。取钢筋混凝土的容重为25kN/m3。已知完建情况下作用荷载和力矩计算见表3.6。

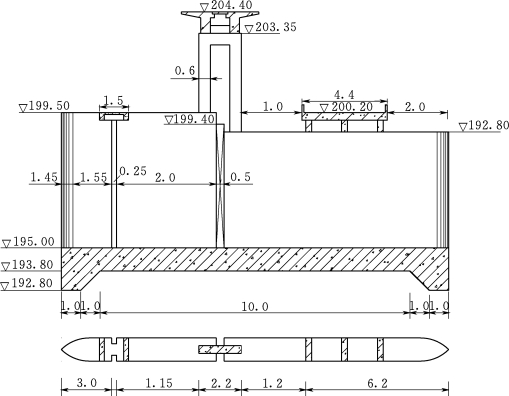
图3.118　闸室结构布置图（单位：m）

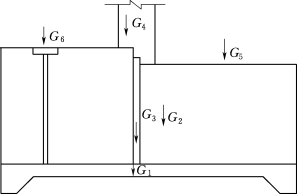
图3.119　完建情况下荷载作用图

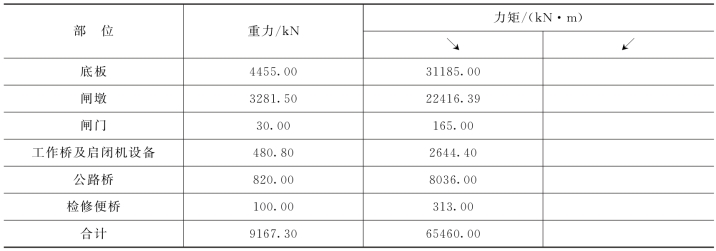
表3.6　完建情况下作用荷载和力矩计算

（2）设计洪水情况。在设计洪水情况下，闸室的荷载除完建期作用荷载之外，还有闸室内水的重力G7，上游水压力P1、P2，下游水压力P3，扬压力（包括浮托力F和渗透压力U）等（图3.120）。

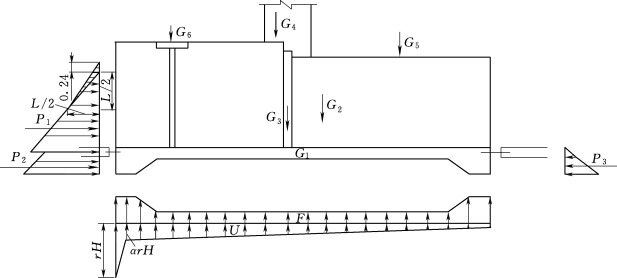
图3.120　设计洪水情况下的荷载图

设计洪水情况下的荷载和力矩计算见表3.7。

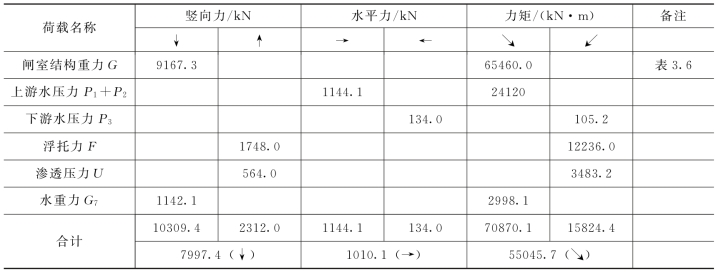
表3.7　设计洪水情况下荷载和力矩计算

（3）校核洪水位情况。校核洪水位情况时的荷载与设计洪水位情况的荷载计算方法相似。所不同的是水压力、扬压力是相应校核水位以下的水压力、扬压力。

校核洪水情况下的荷载和力矩计算见表3.8。

表3.8　校核洪水情况下荷载和力矩计算

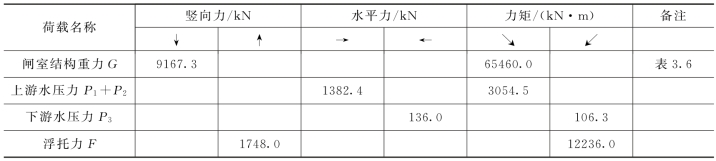
续表

解：

（1）完建期。由表3.6可知，∑G=9167.3kN，∑M=65460.0kN·m，B=14.0m，A=14×9=126（m2），则

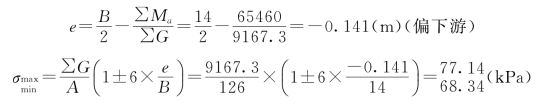
σmin=68.34kPa（上游端）；σmax=77.14kPa（下游端）

（2）设计洪水位情况。

由表3.7可知，∑G=7997.4kN，∑M=55045.7kN·m，∑P=1010.1kN，则

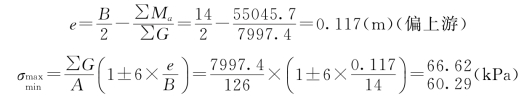
σmin=60.29kPa（下游端）；σmax=66.62kPa（上游端）

（3）校核洪水位情况。由表3.8可知，∑G=8098.8kN，∑M=55657.0kN·m，∑P=1246.4kN，则

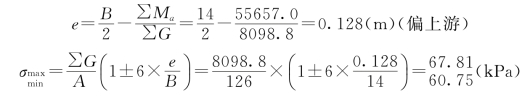
σmin=60.75kPa（下游端）；σmax=67.81kPa（上游端）

【工程实例3】小浪底水利枢纽工程

黄河小浪底水利枢纽工程（图3.121）位于河南省洛阳市孟津县，是黄河干流上的一座集减淤、防洪、防凌、供水灌溉、发电等为一体的大型综合性水利工程，是治理开发黄河的关键性工程，属国家“八五”重点项目。总工期十一年，2001年12月31日全部竣工。总装机容量为156万kW，年平均发电量为51亿kW·h；防洪标准由60年一遇提高到千年一遇；每年可增加40亿m3的供水量。小浪底工程由拦河大坝、泄洪建筑物和引水发电系统组成。

图3.121　小浪底枢纽工程

泄洪建筑物包括1座进水塔、3条导流洞改造而成的孔板泄洪洞、3条排沙洞、3条明流泄洪洞、1条溢洪道、1条灌溉洞和3个两级出水消力塘，受地形、地质条件的限制，均布置在左岸。正常溢洪道位于垭口副坝南侧，布置在T型山梁上，由引渠控制闸、泄槽、挑流鼻坎组成，进口高程为258.0m。进口选用有超泄能力的开敞式三孔洞，闸门尺寸为11.5m×17.5m。在库水位为275.0m时泄流量为3744m3/s。

【问题】溢洪道控制段应力分析。

分析：溢洪道（图3.122）是水库等水利建筑物的防洪设备，包括进水渠、控制段、泄槽和出水渠等，多筑在水坝的一侧，像一个大槽，当水库里水位超过安全限度时，水就从溢洪道向下游流出，防止水坝被毁坏。

图3.122　溢洪道

溢洪道控制段闸室基底应力计算与水闸闸室基底应力计算一样，采用材料力学偏心受压公式计算，考虑到闸墩和底板在顺水流方向的刚度很大，闸室基底应力可近似地认为呈直线分布。

解：

计算公式与水闸闸室基底应力计算公式相同。

【例题】某溢洪道，堰体采用低实用堰，结构布置如图3.123所示。堰顶高程为222.0m，堰体总长为21.0m。堰体表面0.8m厚采用C20钢筋混凝土，堰体内部采用C15素混凝土填筑。

闸室共五孔，单孔净宽12m，总宽度为70.0m，闸室长25.5m，闸墩顶高程为236.3m，高于水库2000年校核洪水位235.56m。闸室为开敞式实用堰结构，设五扇弧型钢闸门，闸门高9.5m，门顶高程为231.33m，采用卷扬启闭机控制。中墩厚度为2.5m，底部和两侧堰体浇筑成一体，单孔基础总宽度为14.5m。边墩为衡重式侧墙，和边孔堰体整体连接，墩顶宽度为1.5m，底宽3.25m，墙背坡度1∶0.3，衡重台高程为225.0m，边墩底部型式同中墩。闸顶上游设汽-10级交通桥连接两岸交通，桥宽5.0m，交通桥中心线桩号0+006.2。交通桥后墩顶抬高，上部设启闭机操纵室，宽6.0m，底板高程241.9m。已知边墩完建期各荷载计算见表3.9，试对溢洪道控制段边墩闸底进行应力计算。

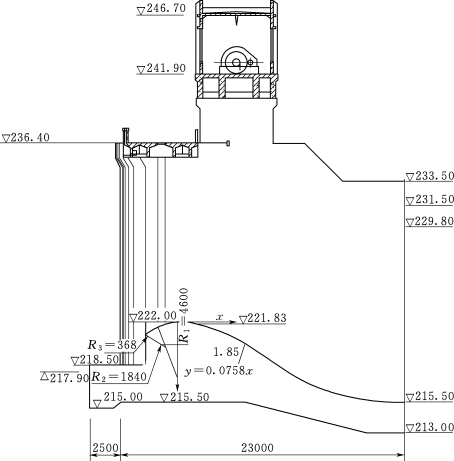
图3.123　溢洪道控制段结构布置图

表3.9　边墩完建期各荷载

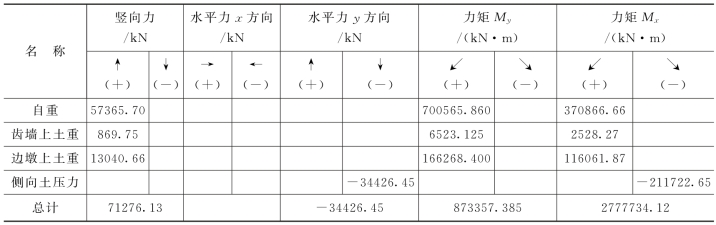
解：

Px=0（kN）　Mx=277734.15（kN·m）

Py=-34426.45（kN）　My=873357.385（kN·m）

G=71276.13（kN）　A=25.5×8.875=226.31（m2）

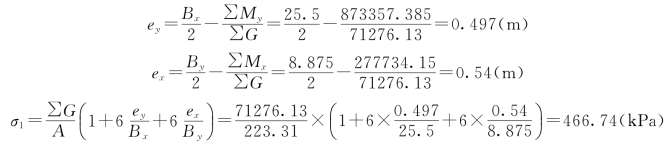
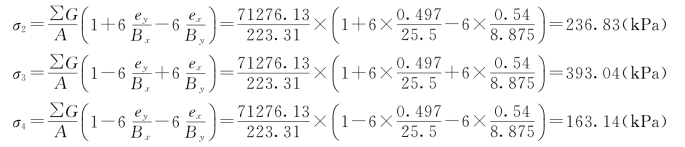
【工程实例4】小湾水电站

小湾水电站（图3.124）位于云南省西部南涧县与凤庆县交界的澜沧江中游河段，是澜沧江中下游河段规划中的第二级电站。该工程主要由混凝土双曲拱坝、坝后水垫塘和二道坝、右岸地下厂房、左岸泄洪洞组成。其中拱坝坝顶高程为1245m，最大坝高为292m，坝顶长992.74m；拱冠梁底宽69.49m，拱冠梁顶宽13m。坝身设5个开敞式表孔溢洪道、6个泄水中孔和2个放空底孔。设计洪水位时枢纽总泄量为17680m3/s，校核洪水位时为20680m3/s（其中，坝身表孔泄8625m3/s，中孔泄6730m3/s，左岸泄洪洞泄5325m3/s）。

图3.124　小湾水电站

【问题】拱坝圆弧拱拱圈厚度和中心角讨论。

分析：拱坝（图3.125）是一空间壳体结构，坝体结构可近似看作由一系列凸向上游的水平拱圈和一系列竖向悬臂梁所组成。坝体结构既有拱作用又有梁作用。其所承受的水平荷载一部分由拱传至两岸岩体，另一部分通过竖直梁传到坝底基岩。

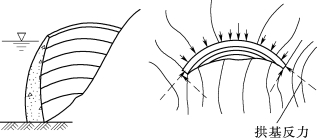
图3.125　拱坝示意图

拱坝两岸的岩体部分称作拱座或坝肩；位于水平拱圈拱顶处的悬臂梁称作拱冠梁，一般位于河谷的最深处。

合理的拱圈型式应当是压力线（拱各横截面上合力作用点的连线）接近拱轴线，使拱截面内的压应力分布趋于均匀。在河谷狭窄而对称的坝址，水压荷载的大部分靠拱的作用传到两岸，采用圆弧拱圈，在设计和施工上都比较方便。但从水压荷载在拱梁系统的分配情况看（图3.126），拱所分担的水荷载沿拱圈并非均匀分布，而是从拱冠向拱端逐渐减小。近年来，对建在较宽河谷中的拱坝，为使拱圈中间部分接近于均匀受压，并改善坝肩岩体的抗滑稳定条件，拱圈型式已由早期的单心圆拱向三心圆拱、椭圆拱、抛物线拱和对数螺旋线拱等多种型式（图3.127）发展。

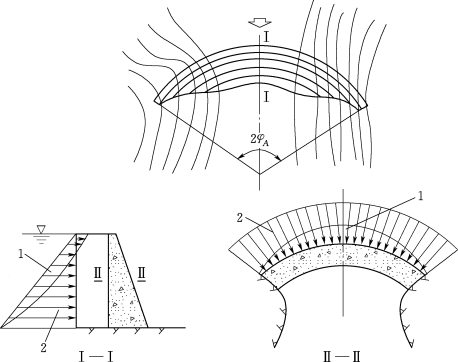
图3.126　拱坝平面及剖面图

1-拱荷载；2-梁荷载

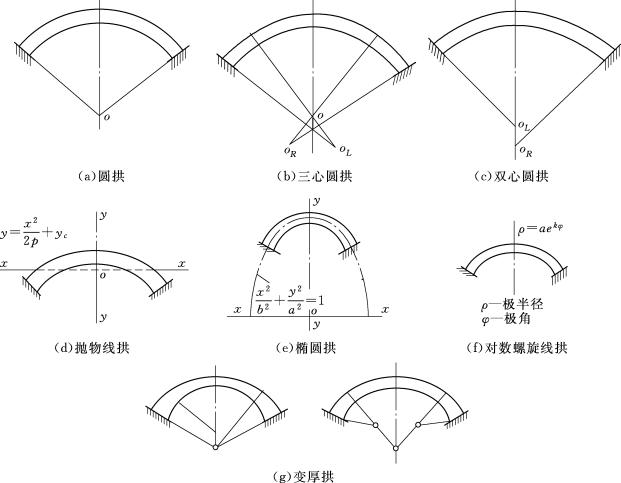
图3.127　拱坝的水平拱圈型式

由于圆弧形水平拱圈最常见，如图3.128所示，圆弧拱圈计算公式分析如下。

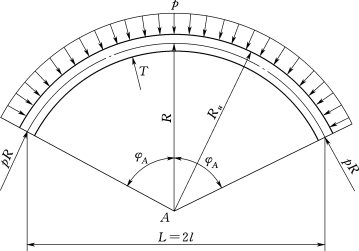
图3.128　圆弧拱圈

解：

取单位高度的等截面圆拱，拱圈厚度为T，中心角为2φA，设沿外弧承受均匀压力p，截面平均应力为σ，竖直方向列平衡方程：

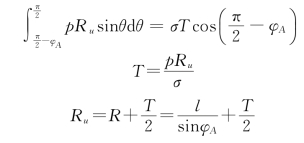
式中：T为拱圈厚度；σ为拱圈截面的平均应力；l为拱圈平均半径处半弦长；Ru、R分别为外弧半径、平均半径。

【例题1】如图3.129所示，设有一固端圆拱厚度T=10m，中心角为2φ，均布压力为1000kN/m2，已知拱冠推力H0=102000kN，拱冠弯矩M0=51836kN·m，拱冠径向变位（Δr）c=0.09658m，求拱冠上、下游面的轴向应力。

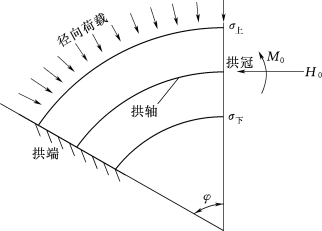
图3.129　拱圈受力简图

解：

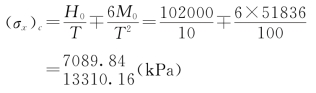
【例题2】某水电站主厂房排梁柱（图3.130）为二级建筑物，柱上端连接预制横梁（接头处用预埋铁件互相焊接，故可视为铰接点），柱下端固接在大体积混凝土上，承受基本荷载。所承受的荷载有：

（1）静荷载。

1）房顶传来的自重P1。

2）吊车梁传来的自重P2。

3）圈梁传来的砖墙及圈梁的自重P3。

4）上柱自重P4，下柱自重P5。

（2）活荷载。

1）房顶活荷载Q2。

2）吊车垂直荷载Qmax及Qmin。

3）吊车横向水平制动力T。

（3）风荷载W。

排架柱受力如图3.131所示，排架计算简图如图3.132所示，根据结构力学方法计算内力，其结果列于表3.10。柱采用一阶变截面，上柱（牛腿以上）截面b×h=40cm×60cm，下柱截面b×h=40cm×90cm。混凝土抗拉强度Rc=12300kPa，混凝土抗压强度Rw=15300kPa。试对排架进行强度校核。

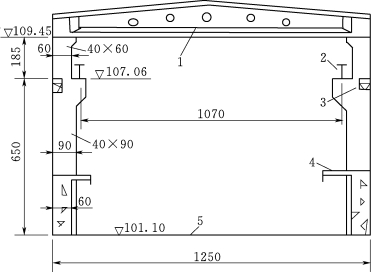
图3.130　某水电站主厂房排梁柱（单位：cm）

1-横梁；2-吊车梁；3-圈梁；4-发电机层；5-水轮机层

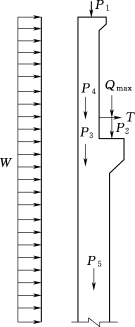
图3.131　排架柱受力图

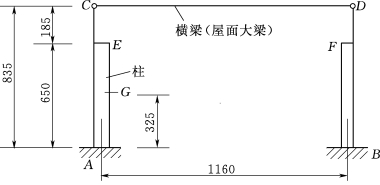
图3.132　排架计算简图（单位：cm）

表3.10　控制截面内力

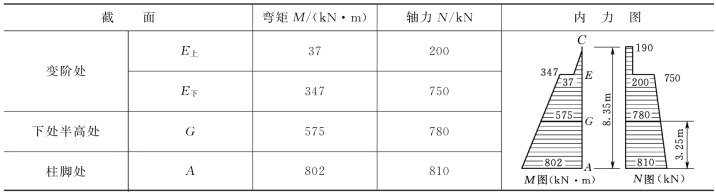
解：

排架受力为压缩和弯曲的组合，应力计算如下。

（1）E截面的应力为

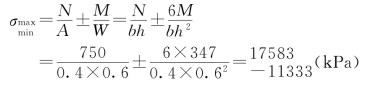
σmax=17583（kPa）＞Rw=15300（kPa）

σmin=11333（kPa）＞Rc=12300（kPa）

排架强度不满足要求，需要加配钢筋。

（2）A截面的应力为

σmax=17102（kPa）＞Rw=15300（kPa）

σmin=12602（kPa）＞Rc=12300（kPa）

排架强度不满足要求，需要加配钢筋。

【例题3】起重能力为80kN的起重机，安装在混凝土基础上（图3.133）。起重机支架的轴线通过基础的中心。已知起重机的自重为180kN（荷载P及平衡锤的重量Q不包括在内），其作用线通过基础底面的轴Oz，且有偏心距e=0.6m。若矩形基础的短边长为3m，问：

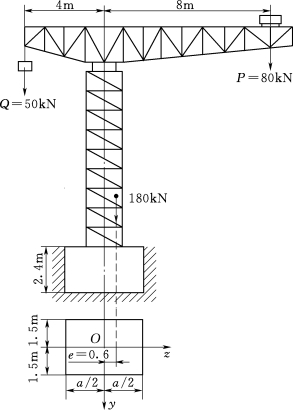
图3.133　[例题3]图

（1）其长边尺寸a应为多少才能使基础上不产生拉应力？

（2）在所选的a值之下，基础底面上的最大压应力等于多少（已知混凝土的密度ρ=2.243×103kg/m3）？

解：

（1）将有关各力向基础的中心简化，得到轴向压力

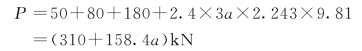
对主轴Oy的力矩为

M=-50×4+180×0.6+80×8=548（kN·m）

要使基础上不产生拉应力，必须使σmin==0。将N=P，A=3a，M和W=代入，可得(www.daowen.com)

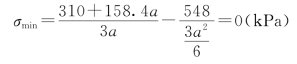
从而解得a=3.68m，取a=3.7m。

（2）在基础底面上产生的最大压应力

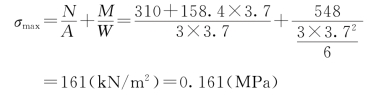
【例题4】某水库溢洪道的浆砌石挡土墙如图3.134所示（墙高与基宽的比例尺未画成一致），通常是取单位长度（1m）的挡土墙来进行计算。已知：墙的自重为G=G1+G2，G1=72kN的作用线到横截面BC的形心O的距离为x1=0.8m，G2=77kN的作用线到点O的距离为x2=0.03m；在横截面BC以上的土壤作用在墙面上的总土压力E=95kN，其作用线与水平面的夹角θ=42°，其在墙面上的作用点D到点O的水平距离和竖直距离分别为xO=0.43m和yO=1.67m；砌体的许用压应力为3.5 MPa，许用拉应力为0.14 MPa。要求计算出作用在截面BC上点B和点C处的正应力并进行强度校核。

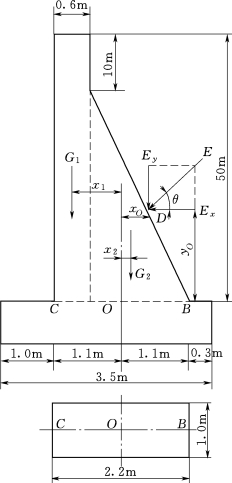
图3.134　某水库溢洪道的浆砌石挡土墙

解：

（1）土压力E的水平分力和竖直分力分别为

Ex=Ecosθ=95cos42°=70.6（kN）

Ey=Esinθ=95sin42°=60.7（kN）

作用在横截面BC上的全部竖向压力为

N=G1+G2+Ey=72+77+63.7=212.7（kN）

各力对横截面BC的形心O的总力矩为

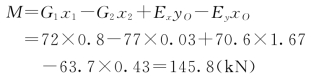
横截面BC的面积（按1m长的挡土墙计算）A=1×2.2=2.2（m2），其抗弯截面模量为

（2）由压弯组合变形应力计算公式可求得点C处的正应力

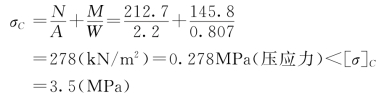
点B处的正应力

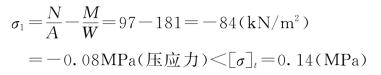
故截面BC满足强度要求。

【例题5】如图3.135所示挡土墙墙高l=3m，厚度h=2m，墙体很长，设土壤对每米长墙体的水平总压力H=30kN，作用在离基础面1/3的墙体高度处。墙体容重为20kN/m3，求基础面上的最大压应力。

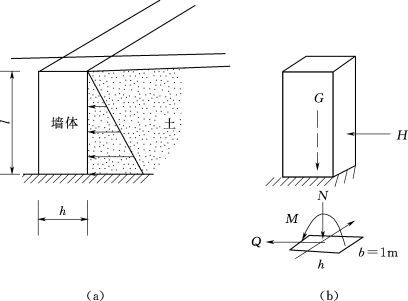
图3.135　挡土墙示意图及受力分析

解：

（1）力学模型机受力分析。由于墙体很长，不可能按全长计算，但每单位长度的受力情形完全相同，所以可以取单位长度为1m的一段墙体来进行计算，如图3.135（b）所示，这段墙体受自重G及土体的水平推力H作用[注：沿墙长方向的墙体相互之间不受力；土体对墙作用的侧向分布压力，类似水压力，越深越大，近似地可以看做沿深度呈斜线分布，如图3.135（a）所示，故其合力H的作用点在离地面的1/3墙体高度处]。

（2）内力。墙体受自重及水平力作用，危险截面在底面，其受力如图3.135（b）所示。其中：

轴力为

N=1×2×3×20=120（kN）

弯矩为

剪力为

Q=H=30（kN）

（3）最大应力。底截面受压弯组合，危险点为截面的左侧边缘，此处剪应力为零。所以在截面左、右两侧有正应力极值：

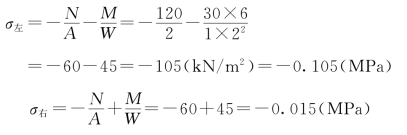
【例题6】矩形截面柱受纵向压力F1、F2作用，如图3.136所示，F1的作用线与柱轴重合，F2的作用线与柱轴平行且作用点落于y轴上，F1=100kN，F2=45kN，b=180mm，F2的偏心距e=200mm。求：

（1）欲使柱的横截面上不出现拉应力，截面尺寸h最小应为多少？

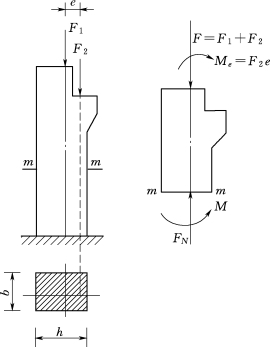
图3.136　矩形截面柱受力图

（2）当h确定后求柱截面上的最大压应力。

解：

由于纵向力的合力偏离截面形心，柱的变形为偏心压缩。将力F2移至F1作用线处，附加外力矩为

Me=F2e=45×200（kN·mm）=9×103（N·m）

截面中的内力为

FN=F1+F2，M=Me

（1）若使截面上不出现拉应力，则有

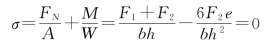
解得

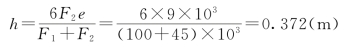
（2）柱截面上的最大压应力为

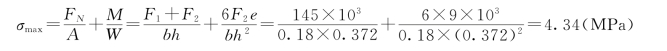
【例题7】等截面石砌圆端形桥墩如图3.137所示，梁及车辆的压力为P1=1500kN，列车的制动力为P2=180kN，上游流水压力为q=15kN/m。已知石料容重γ=22kN/m3，横截面的Iz=4.63m4，Iy=2.12m4，求桥墩的最大压应力及其所在位置。

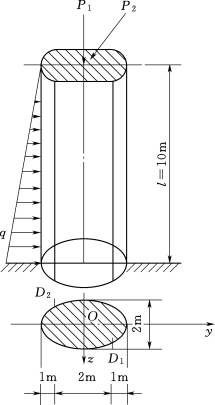
图3.137　等截面石砌圆端形桥墩

解：

（1）计算危险截面（桥墩底截面）上的内力。

自重为

轴力为

N=P1+G=1500+1571=3071（kN）

弯矩为

My=P2l=180×10=1800（kN·m）

（2）将桥墩底截面上诸内力换算成一个偏心力P，并求其偏心距。

偏心力为

P=N=3071（kN）

偏心距为

（3）求中性轴的截距。设中性轴在y和z轴上的截距分别为ay和az。于是

又

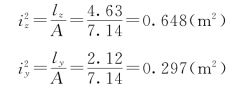
故

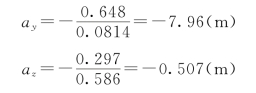
（4）作与中性轴平行且与截面相切的直线，可得切点D1及D2，D1点发生最大压应力，其坐标值约为

（5）计算最大压应力。

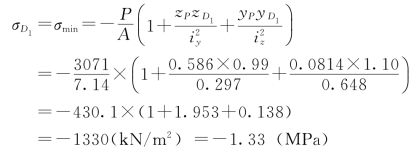
【例题8】斜梁AB（如楼梯梁）在跨度中央受竖向集中力P作用如图3.138所示。求梁的最大压应力值及发生位置。

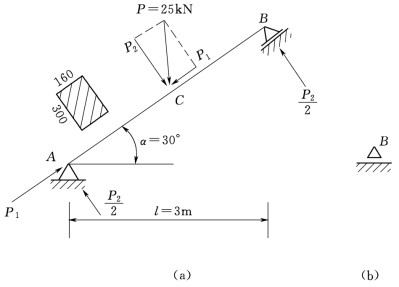
图3.138　斜梁受力图

解：

将力P沿梁的轴线及与它垂直方向分解，得

P1=Psinα

P2=Pcosα

显然，P1使梁的AC段压缩，P2使斜梁AB弯曲，故最大压应力发生在截面C的左侧的上缘。

最大弯矩为

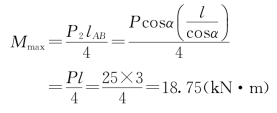
它相当于斜梁在水平面上投影的简支梁的最大弯矩。

梁的抗弯截面模量为

最大压应力的值为

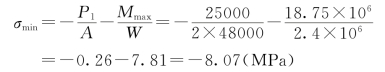
讨论：若斜梁的支座B只能产生竖向的支座反力，如图3.138（b）所示，则梁的最大弯矩不变（还是相当于斜梁在水平面上投影的简支梁的跨中弯矩），只是斜梁内的轴力N有变化，下半段受压，上半段受拉，其值各为P1的一半。

【例题9】有一盖板式涵洞是用容重为γ=24kN/m3的材料做成的。设涵洞的形式、尺寸以及荷重情形如图3.139所示。试求涵洞边墙上C、D两点的应力。

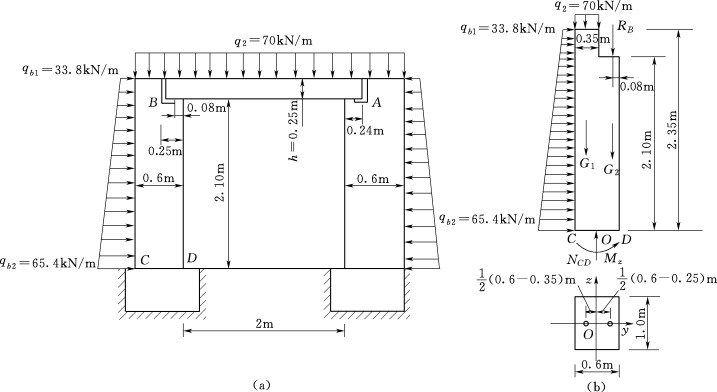
图3.139　某盖板式涵洞示意图及计算简图

解：

（1）盖板传给边墙的内力RA、RB为

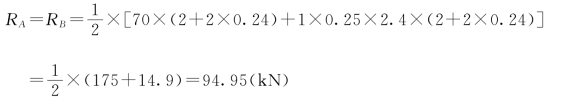
RA、RB的作用点离开边墙内侧面边缘的距离为支承宽度的，即×0.24=0.08（m）。

（2）求作用在CD截面上的内力[图3.139（b）]。轴向压力

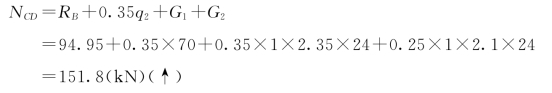
CD截面上z轴的弯矩（以顺时针为正方向）

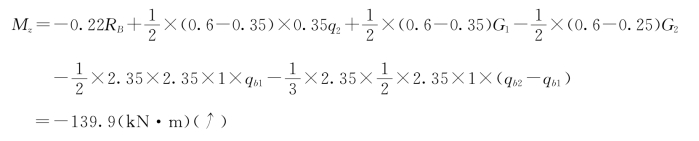
（3）C、D两点的应力

【小结】

对拱坝：

（1）当应力条件相同时，拱中心角2φA越大（即R越小）拱圈厚度T越小，就越经济。但中心角增大也会引起拱圈弧长增加，抵消了一部分由减小拱厚所节省的工程量。可以计算出拱圈体积最小时的中心角：2φA=133°34′。

（2）当拱厚T一定，拱中心角越大，拱端应力条件越好。采用较大中心角比较有利，但选用很大的中心角将很难满足坝肩稳定的要求。

（3）从有利于拱座稳定的角度考虑，要求拱端内弧面切线与可利用岩面等高线的夹角不得小于30°。过大的中心角将使拱端内弧面切线与岩面等高线的夹角减小，对拱座稳定不利。因此，拱圈中心角在任何情况下都不得大于120°。

（4）一般情况下可使顶拱中心角采用实际可行的最大值，往下拱圈的中心角逐渐减小。坝体顶拱最大中心角应根据不同的水平拱圈型式，采用90°～110°，底拱中心角在50°～80°之间选取。

习题

1.起重机受力如图3.140所示，F1=30kN，F2=220kN，F3=60kN，它们的作用线到立柱中心线的距离分别为10m、1.2m和1.6m。如立柱为实心钢柱，材料的许用应力[σ]=160MPa，试设计其底部A-A处的直径。

2.如图3.141所示一浆砌块石挡土墙，墙高4m。已知：墙背承受的土压力Pa=137kN，且其作用线与竖直线之间的夹角α=45.7°，浆砌块石的密度ρ1=2.345×103kg/m3，墙基混凝土的密度ρ2=2.396×103kg/m3，其他尺寸如图3.141所示。试取1m长的墙作为计算对象，求墙上A、B、C、D各点处的正应力。

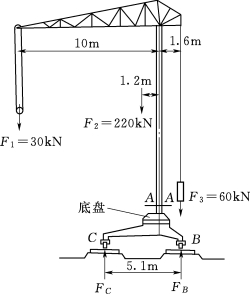
图3.140　起重机受力图

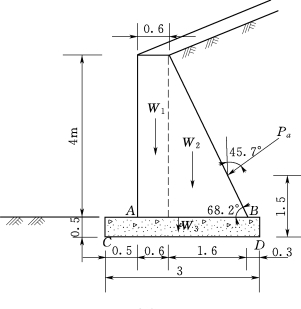
图3.141　浆砌块石挡土墙受力图（单位：m）

3.如图3.142所示的混凝土重力坝，剖面为三角形，坝高为h=30m，混凝土的密度为2.396×103kg/m3。若只考虑上游水压力及坝体自重的作用，在坝底截面上不允许出现拉应力，试求所需的坝底宽度B和在坝底上产生的最大压应力。

4.有一横截面为矩形、支撑沙土填方的砖砌挡土墙（图3.143）。如果砖砌容重γ=20kN/m3，填土给墙的水平压力按三角形规律分布，且每米长的墙承受压力P=50kN。试求：

（1）墙基平面上的最大拉应力和最大压应力。

（2）欲使此墙不受拉应力，则其厚度x应需多少？

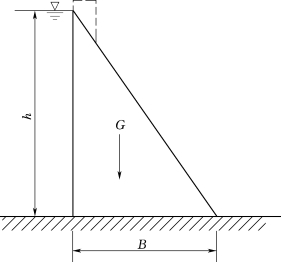
图3.142　混凝土重力坝剖面图

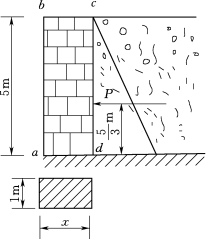
图3.143　砖砌挡土墙示意图

5.挡住泥土的土墙如图3.144所示。墙体的容重γ=18kN/m3，泥土的压力q是水平方向的，并且沿墙的高度按三角形规律分布，在墙根的最大的压力qmax=15kN/m3。试求墙底的最大和最小压应力。

6.如图3.145所示为两种高为H=7m的混凝土堤坝的横截面。若取混凝土的容重为γ=20kN/m3，为使堤坝的底部不受拉应力，试求坝必须的宽度a1和a2。

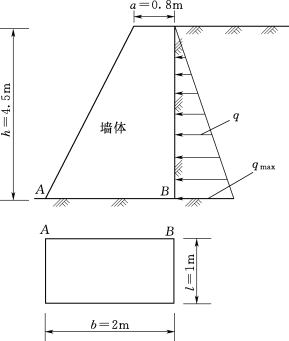
图3.144　挡泥土的土墙示意图

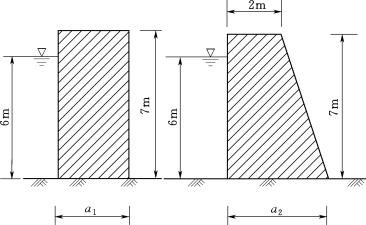
图3.145　混凝土堤坝的剖面图

7.有一圆柱形塔（图3.146），高为H，内径为d1，外径为d2，并有微小倾斜。试问与竖直线所成最大许用倾角α为多少时，才能使塔中不产生拉应力（仅考虑塔的自重荷载）？

8.如图3.147所示为某浆砌石挡土墙，墙高4m，已知墙背承受土压力F=137kN，并且与铅垂线成α=45.7°，浆砌石的重度为23kN/m3，其他尺寸如图3.147所示，试取1m长墙体作为计算对象，计算AB截面上A点与B点的正应力，又砌体的许用压应力[σ-]为3.5MPa，许用拉应力[σ+]为0.14MPa，试做强度校核。

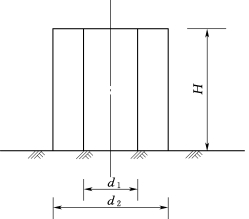
图3.146　圆柱形塔示意图

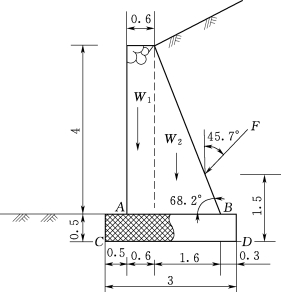
图3.147　某浆砌石挡土墙受力图（单位：m）

9.如图3.148所示混凝土坝的高度为h，坝外水面与坝顶相平，设混凝土坝不能抵抗拉应力，又知混凝土的密度是水的2.5倍，试按以下两种情况计算坝所需的厚度。

（1）坝截面为矩形。

（2）坝截面为三角形。

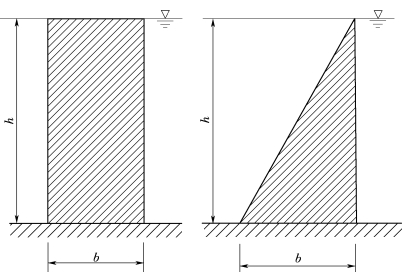
图3.148　两种情况混凝土坝示意图

10.厂房的边柱，受屋顶传来的荷载P1=120kN及吊车传来的荷载P2=100kN作用，柱的自重G=77kN，底截面如图3.149所示。求：

（1）底截面上的正应力分布图。

（2）若在柱的左侧又受到墙壁传来的向右风力q=1kN/m作用，求底截面上的正应力分布图。

11.如图3.150所示为某渡槽的空心墩。已知：墩上承受的水重W3=2400kN，渡槽槽身重W2=2143kN，在截面AB以上部分墩身的自重W1=5115kN，风压力对截面AB上y-y轴产生的力矩My=7514kN·m，截面AB的面积A=4.67m2，抗弯截面模量Wz=6.42m3。试求作用在截面AB上的最大正应力和最小正应力。

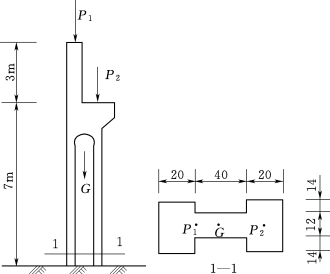
图3.149　厂房边柱示意图（单位：cm）

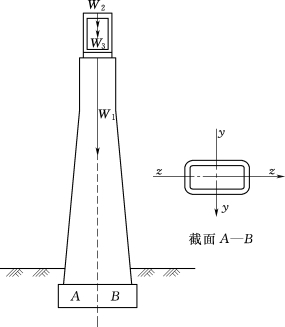
图3.150　某渡槽的空心墩示意图

12.如图3.151所示某厂房柱子，受到起重机梁的铅垂轮压F=220kN，屋架传给柱顶的水平力Fx=8kN，及风荷载q=1kN/m的作用。力F的作用线离柱的轴线的距离e=0.4m，柱子底部截面为矩形，尺寸为1m×0.3m，试计算柱子底部危险点的应力。

13.如图3.152所示为某渡槽刚架的基础。已知：在它的顶面上受到由柱子传来的弯矩M=110kN·m，轴力N1=980kN和水平剪力Q=60kN，基础的自重和基础上土重的总重为N2=173kN。试作出在基础底面的反力分布图（假定反力是按直线规律分布的）。

图3.151　某厂房柱子示意图

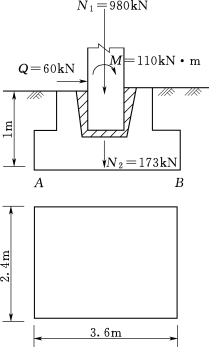
图3.152　某渡槽刚架的基础示意图

14.某混凝土桩基础，受偏心压力F=1000kN作用，偏心距e=0.5m。由15根木桩支承，桩的排列如图3.153所示。假设桩的直接d=15cm。求力F作用下，左右两侧最边一排木桩中每根桩所受压力等于多少？

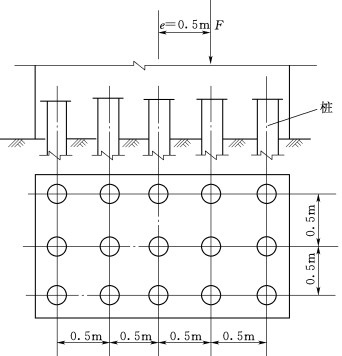
图3.153　某混凝土桩基础示意图

15.如图3.154所示为两座水坝的截面，一为矩形，一为三角形。水深均为l，混凝土密度ρ=2.2×103kg/m3。试问当坝底截面上不出现拉应力时h各等于多少l？

16.砖墙和基础如图3.155所示。设在1m长的墙上有偏心力P=40kN的作用，偏心距e=0.05m。试绘1-1、2-2、3-3截面上的正应力分布图（自重不计）。

图3.154　水坝截面示意图

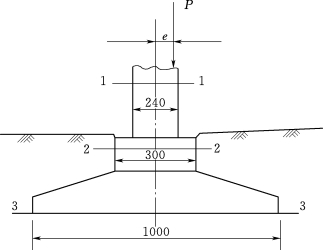
图3.155　砖墙基础示意图

17.为什么计算拱圈厚度和中心角时假定拱圈截面上的应力是均匀分布的，计算拱冠梁截面时假定应力分布是线性的？