【问题】水流作用在水轮机转轮上的转动力矩计算。

分析：反击式水轮机同时利用了水流的势能与动能，水流通过蜗壳均匀分布到转轮周围，轴对称地进入水轮机[图2.116（a）、（b）]。水流充满整个转轮的空间，在转轮叶片约束下改变流速与方向，从而对转轮叶片产生反作用力，驱动转轮旋转。通过水轮机水流的大部分动能与势能都转换成转轮旋转的机械能。

图2.116　水流作用在水轮机转轮上的受力分析

进转轮水流方向与大小；产生升力方向与大小；--→转轮旋转方向；水流对叶片的相对方向与大小

混流式水轮机的转轮[图2.116（c）]看起来较复杂，水流从水轮机四周水平方向向中心流入转轮（径向进入），然后转为向下方向出口[图2.116（d）]，水流进入转轮内在向轴芯方向通过叶片时推动转轮，同时在向下通过叶片时也推动转轮，也就是说水流在径向与轴向通过叶片时都做功[图2.116（e）]，故称为混流式水轮机。

【例题1】水轮机转轮在水流的冲击下以匀角速度ω绕铅垂轴O转动，如图2.117所示。设水流进蜗壳的总流量为Q，水的密度为ρ，水流进转轮和离开转轮的绝对速度分别为v1及v2，与轮缘切线夹角方向分别为a1及a2，转轮的外圆与内圆的半径分别为r1与r2。假定水流为恒定流，试求水流作用在转轮上的转动力矩。

图2.117　水轮机受力分析

解：

由于水流为恒定流，流进蜗壳的总水流量就是流进转轮的流量，设流进两叶片间的水流量为q，则Q=∑q。

取转轮上两个叶片间的水体（图2.117中的ABCD部分）为研究的质点系。作用在质点系上的外力有：水体的重力和叶片对水体的反力。而重力与转轴z（z轴与图2.117平面垂直）平行，它对转轴z的矩为零，所以两叶片对水流的反力对于z轴的矩m′在数值上等于水流作用在两叶片上的力矩mzi。应用质点系动量矩定理得

下面计算在dt时间内，ABCD水体对固定点O的动量矩的改变量dHzi。设在瞬时t水体在ABCD位置，在瞬时t+dt，它运动到abcd新位置，如图2.117（b）所示。则在dt时间内水体对z轴的动量矩的改变量为

将式（b）代入式（a）后，得到两叶片对水流的反力对于z轴的转动力矩为

对于转轮整体（全部叶片），转轮作用于水体的转动力矩为

或

根据作用力与反作用力定律，全部水流作用在水轮机转轮上的转动力矩，即

(www.daowen.com)

【例题2】卷扬机鼓轮重Q，半径为R，可绕经过鼓轮中心O的水平轴Oz转动，如图2.118所示。鼓轮上绕一绳，绳的一端挂一重P的物体。今在鼓轮上作用一力矩M以提升重物，求重物上升的加速度。鼓轮可看作均质圆柱，绳的重量及轮轴处的摩擦都不计。

图2.118　卷扬机示意图

解：

将鼓轮与重物作为一个质点系来考虑，作用于该质点系的外力有：已知的重力P、Q及力矩M；轮轴处的未知约束力N。约束力N通过轮轴Oz，因此，如以Oz为矩轴而应用动量矩定理求解，则方程中将不包含未知力N，可直接求得加速度。

设重物上升的速度为v，鼓轮的角速度为ω，则整个质点系对于z轴的动量矩为

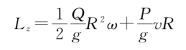
但ω=v/R，所以

外力对z轴的矩为

于是根据动量矩定理有

由此可得重物上升的加速度

习题

1.如图2.119所示通风机的转动部分以初角速度ω0绕中心轴转动，空气的阻力矩与角速度成正比，即M=kω，其中k为常数。如转动部分对其轴的转动惯量为J，问经过多少时间其转动角速度减少为初角速度的一半？又在此时间内共转过多少转？

2.图2.120所示为一卷扬机。鼓轮为均质圆盘，重为P，半径为R，可绕经过鼓轮中心O的中心轴Z转动。小车和车上材料总重为Q。作用在鼓轮上有一力矩M，轨道的倾角为α。绳的重量及摩擦均忽略不计。求小车上升的加速度。

图2.119　通风机的转动部分示意图

图2.120　卷扬机工作图