【工程实例1】石头水电站

石头水电站位于黑龙江省宁安县中部石岩乡境内牡丹江上，为河床式小水电站。坝址控制流域面积为1.4万km2。电站由拦江坝、泄洪闸、进水闸、厂房等建筑物组成。拦江坝为浆砌石溢流坝（图2.104），长123m，高10.6m。

【问题】求溢流坝反弧段动水压力。

分析：在确定溢流坝剖面后，需要对作用在溢流坝面上的各种荷载进行计算，以便确定溢流坝内任一点的应力是否满足强度要求及整个坝体是否满足稳定要求，校核溢流坝的稳定安全性。在荷载计算中，溢流坝的反弧段的动水压力是其中的计算荷载之一。

溢流坝的荷载分析沿坝轴线取单位长度进行研究。如图2.105（a）所示，当溢流坝上闸门打开，水流从坝顶下泄，流过溢流坝面时，对溢流坝面会产生动水压力。动水压力的计算可采用质点系动量定理来分析。

解：

反弧段动水压力的分布如图2.105（b）所示，把分布力分解为相互垂直的两个分力，由于作用面为曲面，计算分布力分解后的总合力。

图2.104　石头水电站溢流坝

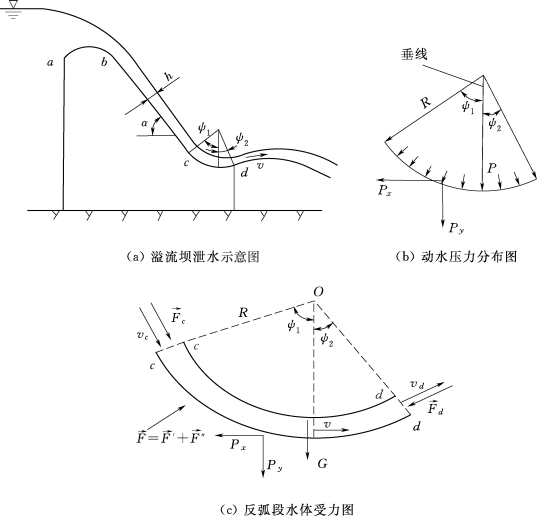
图2.105　溢流坝反弧段受力分析

取c-c截面和d-d截面段水流作为研究对象[图2.105（c）]，利用质点系动量定理（在某一时间间隔内，质点系动量的改变量等于在这段时间内作用于质点系外力冲量的矢量和），得

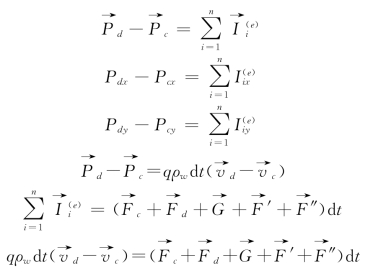
由平衡条件得

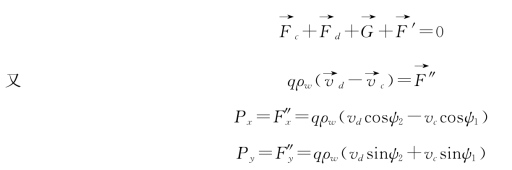
假定在反弧段上的v是常数，在一般溢流重力坝中，这样假定的误差不大，在反弧段单位宽度上动水压力总合力的水平及垂直分力如下：

水平动水压力：　Px==qρwv（cosψ2-cosψ1）

垂直动水压力：　Py==qρwv（sinψ2+sinψ1）

以上式中：为反弧段水流重力；为相邻水流对反弧段上水流的压力；为与外力相平衡的水流对反弧段静约束力；为由于水流的动量变化而产生的附加动约束力；vc、vd为c-c断面、d-d断面平均流速，m/s；Px为动水压力的水平分量，kN；Py为动水压力的竖直分量，kN；ρw为水的密度；kg/m3；P为动水压力强度，Pa，方向与反弧面垂直；q为单宽流量，m3/（s·m）；v为反弧最低点的断面平均流速，m/s。

【工程实例2】引水压力钢管水锤

俄罗斯萨扬-舒申斯克水电站（图2.106）位于俄罗斯西伯利亚叶尼塞河上游，总装机容量为10×64万kW，电站挡水建筑物为混凝土重力拱坝，厂房布置在坝后，采用单管单机引水发电。压力管道为外包混凝土坝后背管，直径为7.5m。水轮机为混流式，转轮直径为6.77m，额定水头为194m，额定流量为358m3/s，额定转速为142.8r/min，在最大水头220m时，最大出力为735MW。

图2.106　俄罗斯萨扬-舒申斯克水电站

2009年8月17日8时13分，俄罗斯萨扬-舒申斯克水电站发生了灾难性事故，水电站发电机层以下厂房淹没，2、7和9号机组被摧毁，其余各台机组及厂房设施均有不同程度的严重损毁（图2.107），造成75人死亡，13人受伤。

图2.107（一）　俄罗斯萨扬-舒申斯克水电站事故

图2.107（二）　俄罗斯萨扬-舒申斯克水电站事故

俄罗斯萨扬-舒申斯克水电站事故的直接原因：2号水轮机长期在振动摆度大的状态下运行，顶盖紧固螺栓疲劳损伤失效。其他原因：水轮机稳定运行范围过窄，结构设计存在缺陷，年久失修，关键部件老化；机组自动功率调节（AGC）规则未能全面反映机组的实际运行状态，使“带病”运行的2号机组承担功率调节的首选机组，并频繁穿越不推荐运行区；在机组振动摆度严重超标的状况下，水电站管理者、运行人员未及时发现并采取措施。萨扬水电站7号和9号机组极有可能经历了负荷转移引起的增负荷、电气短路引起的甩负荷、导叶拒动引起的飞逸以及进入不容许运行区机组剧烈振动导致轴系失稳、转子与定子摩擦碰撞、巨大的水锤压力引起的抬机和顶盖张裂等一系列事故。

分析：在水电站运行过程中，为了适应负荷变化或由于事故原因而突然启闭水轮机导叶时，进入水轮机的流量迅速改变。由于水流具有较大的惯性，流速的突然变化使压力水管、蜗壳及尾水管中的压力随之变化，这种交替升降的一种波动，如同锤击作用于管壁，有时还伴随轰轰的响声和振动，这种现象称为水锤。

水锤压力上升过大，会对蜗壳和压力管道结构安全带来影响：①压强升高可以达到很大的程度，甚至引起管道的破裂；②尾水管中负压过大，产生尾水管空蚀，使得水轮机运行时产生振动。由于水锤的危害很大，故在管道及水轮机等工程设计中必须考虑水锤问题。

【问题】如图2.108所示的简单引水管道系统，管道的首部与水库相连，末端装有一可调节流量的阀门，管道长为L，管道直径为D，管壁厚度e沿程不变。设初始时管道水流为恒定流，流速为v0，压强为p0，试运用动量定理分析管道末端阀门突然瞬间关闭时，管道末端的压强变化值，即水锤压强（忽略阻力及二阶微量，并认为ΔpA≫p0ΔA）。

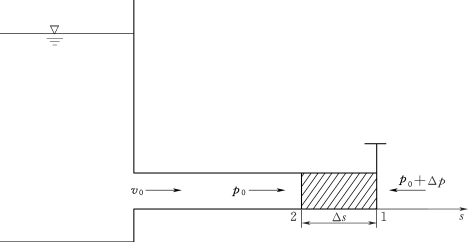
图2.108　简单引水管道系统

解：

如图2.108所示的简单引水管道系统，其管道末端的阀门瞬时完全关闭时，首先是与阀门紧相连的微小段的水流流速为零，这时该微小段水流的动量发生相应的变化，压强增大，液体受到压缩，密度增大，管道受压膨胀。紧连着此微小段的另一微小段内的液体也相应地速度为零、压强增大和受到压缩。并依次一段一段地以波的形式向上游传播，也称为弹性波。其传播速度称为水锤波速，以c表示。

由液体速度的减小，引起压强的增大，所产生的这一压强增量可根据动量定理来确定。

设Δt时间段内，水击波由1断面行进到2断面，受水锤波影响的微小段长度为Δs，此微小段的液体速度由原来的v0减少至v，这时因惯性作用，使压强由p0增大到p0+Δp，密度由ρ增大到ρ+Δρ，管道断面面积由A增大到A+ΔA。

在Δt时间段内，Δs微小段液体的动量变化率为

将上式分子展开，并忽略二阶微量，其动量变化率可写成

同时，微小段所受到的作用力，在不计阻力的情况下，为

p0A-（p0+Δp）（A+ΔA）

根据动量定理，有

忽略二阶微量，并认为ΔpA≫p0ΔA，整理后可得

式中Δs/Δt表示压强变化的传播速度，即水锤波的传播速度，以c表示。故，上式可写为

Δp=ρc（v-v0）

上式为阀门关闭时的水锤压强增量表达式。以重度γ同除上式两边，可得水锤压强的水柱高表示为

(www.daowen.com)

当阀门瞬时完全关闭时，v=0，则

当阀门瞬时完全关闭时，管道所受的压强是很大的。当管道中的初始流速v0=5m/s，波速c=1000m/s，在水电机组甩全负荷时，水锤压力ΔH将达510m，因此在水电站中这种情况是绝对避免发生的。可见在对水电站进行设计时要充分考虑水锤问题，否则会出现严重的后果。

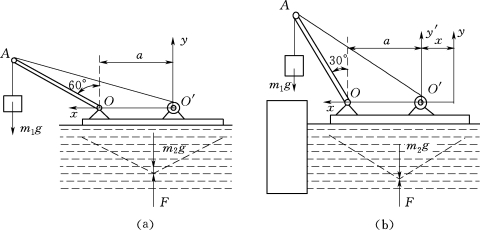
图2.109　浮动起重机示意图

【例题1】如图2.109所示浮动起重机举起质量m1=2000kg的重物。设起重机质量m2=20000kg，杆长OA=8m；开始时杆与铅直位置成60°角，水的阻力和杆重均略去不计。当起重杆OA转到与铅直位置成30°角时，求起重机的位移。

解：

起重机和重物组成的系统，在水平方向不受外力，故系统在水平方向动量守恒，因初始时系统静止，动量为0，所以终止时动量也应为0，如图2.109（b）所示。设起重机速度为v，=r。点A的速度

其中ve=v，vr=，将上式向水平方向投影，得

由x轴方向的动量守恒可得

m1vAx+m2v=0

得

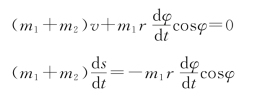
上式中，s、v分别为起重机水平位移和水平方向移动速度，将上式两边积分，得

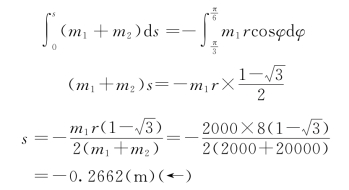
所以起重机左移0.2662m。

【例题2】水流以速度v0=2m/s流入固定水道，速度方向与水平面成90°角，如图2.110所示。水流进口截面积为0.02m2，出口速度v1=4m/s，它与水平面成30°角。求水作用在水道壁上的水平和铅直的附加压力。

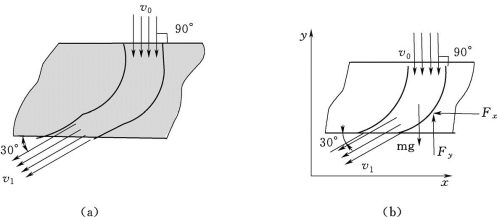
图2.110　水流在固定水道流动示意图

解：

将水道中的水流作为研究对象，管壁对于流体的附加动约束力

ρ=1000kg/m3

由不可压缩流体的连续性定律知

qv=v0A0=v1A1

将式（a）分别向轴x，y投影，得

-Fx=-v0A0v1cos30°ρ

Fy=v0A0[-v1sin30°-（-v0）]ρ

将v0=2m/s，A0=0.02m2，v1=4m/s，代入上式，得

Fx=139N（←），Fy=0

水对管壁作用的附加动压力

方向与Fx方向相反。

习题

1.已知水的体积流量为qv，密度为ρ；水冲击叶片的速度为v1，方向沿水平向左；水流出叶片的速度为v2，与水平线成θ角。求图2.111所示水柱对涡轮固定叶片作用力的水平分力。

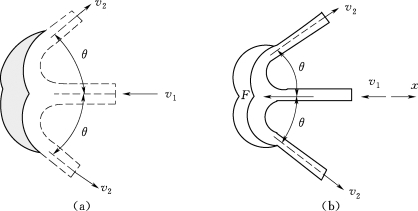
图2.111　习题1图

2.如图2.112所示传送带的运煤量恒为20kg/s，胶带速度恒为1.5m/s。求胶带对煤块作用的水平总推力。

图2.112　习题2图

3.如图2.113所示移动式胶带输送机，每小时可输送109m3的砂子。砂子的密度为1400kg/m3，输送带速度为1.6m/s，设砂子在入口处的速度为v1，方向垂直向下，在出口处的速度为v2，方向水平向右。如输送机不动，问此时地面沿水平方向总的阻力有多大？

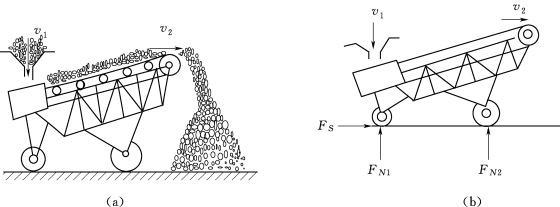
图2.113　习题3图

4.如图2.114所示，施工中广泛采用喷枪浇注混凝土衬砌。设喷枪的直径D=80mm，喷射速度v1=50m/s，混凝土比重γ=21.6kN/m3，求喷浆对壁之压力。

5.压实土壤的振动器，由两个相同的偏心块和机座组成。机座重Q，每个偏心块重P，偏心距e，两偏心块以相同的匀角速ω反向转动，转动时两偏心块的位置对称于y轴。试求振动器在图2.115所示位置时对土壤的压力。

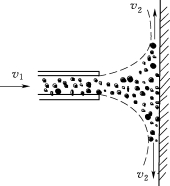
图2.114　习题4图

图2.115　习题5图