【工程实例】三门峡水库

三门峡水库（图2.99）是黄河上第一个大型水利枢纽工程，于1960年9月开始蓄水，在“蓄水拦沙”运用期，最高蓄水位达332.58m，库区泥沙淤积发展迅速，淤积量达17.96亿m3，水库淤积末端出现“翘尾巴”现象，潼关高程（流量为1000m3/s时的水位）比建库前的323.4m急剧抬升了4.5m，导致渭河下游河床不断淤积抬高，使素有“八百里秦川”美称的关中地区、渭河两岸的生态环境恶化，并严重威胁西安市的防洪安全，迫使水库不得不进入改建和改变运用方式阶段。三门峡水库改建工程包括：打开原施工导流洞和增设排沙隧洞等，并两次改变运行方式，严格控制水库在正常运用期的蓄水位。到1973年汛后潼关高程降为326.64m。1973年10月以后，水库采用“蓄清排浑”的方式，即在汛期河水中含沙量大的时候不蓄水，等到了河水变清的时候再蓄水。这种方法使水库淤积和潼关高程得到了有效控制，潼关高程基本维持在327.00m左右。

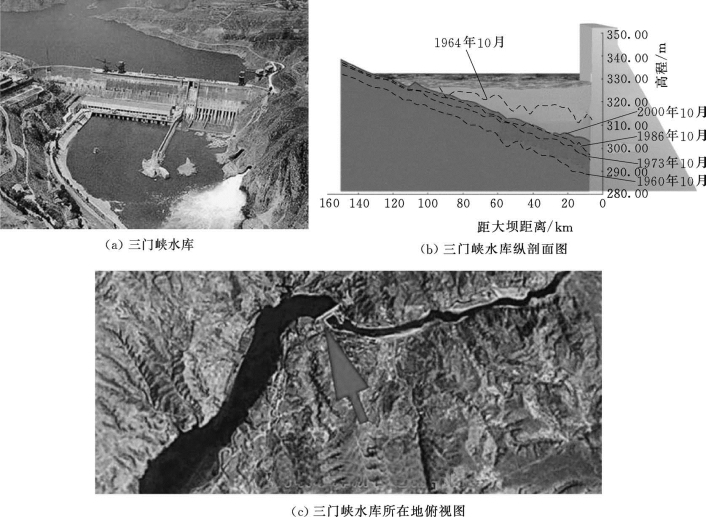
图2.99　三门峡水库

【问题】水库泥沙淤积问题分析。

分析：水流进入库区后，由于水深沿流程增加，水面坡度和流速沿流程减小，因而水流挟沙能力沿流程降低，出现泥沙淤积。泥沙淤积问题是水库建设必然要面对的难题，因为入库后水流趋缓，上游来水中夹带的泥沙将沉降、淤塞库容，缩短水库的使用寿命。泥沙在水库末端淤积，抬高河床，出现“翘尾巴”的现象，严重的会给上游带来新的灾害。泥沙问题处理得好，会延长水库的寿命，充分发挥水库的综合效益；处理不好不仅会影响效益的发挥，还会带来灾害。

【例题】一颗质量为m的泥沙M在水库中由O处自由沉降，如图2.100所示。已知与泥沙同体积的水的质量为m′，水体对匀速下沉的泥沙的运动阻力为R=μv2，v为泥沙的沉降速度，系数μ与泥沙形状、横截面尺寸及水的密度有关。求泥沙的沉降速度及其运动方程。

解：

取泥沙M为研究对象，并视之为质点。泥沙所受的力有：重力W、水的浮力F及运动阻力R。以泥沙运动的初始位置为坐标原点，x轴铅垂向下，如图2.100所示。

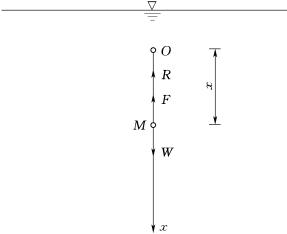
图2.100　水流夹沙颗粒运动示意图

泥沙运动的初始条件为t=0时，x0=0，v0=0。于是其运动微分方程为

即

或

设a=，n=，则式（a）为

在积分之前先就式（b）讨论泥沙的沉降加速度和极限速度问题。

（1）在t=0即运动刚开始时，由于v0x=0，阻力R=0，其加速度为

可见泥沙在水中，ax＜g。若泥沙在真空中沉降，则a=1，ax=g；在空气中，a≈1，ax≈g。

（2）开始沉降后，随着速度vx逐渐增大，阻力R将很快地增加，而加速度ax则很快地减小。当速度达到某一数值时，其加速度为零，此时的速度称为极限速度，以C表示，此后泥沙将保持匀速C沉降。由式（b）得

0=ag-nC2

故

(www.daowen.com)

现在对式（b）积分。由ag=nC2，可将式（b）写成

分离变量后积分：

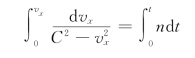
解得

再分离变量后积分：

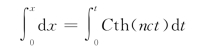
得

将式（d）及n=代入式（e）和式（f），得泥沙的沉降速度及运动方程分别为

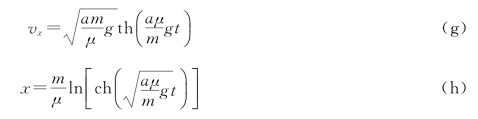
由式（e）可知，沉降速度随时间t的增加而增大，当t→∞时，th（nct）=1，则vx=C，实际上当nct=3.8时，vx=0.999C，可见在很短时间内，泥沙的速度就趋于极限速度了。如nct=2π时，vx=0.9999C≈C，由此可得到泥沙由静止开始下沉达到极限速度所需的时间为

习题

1.如图2.101所示，重Q=100kN的重物用钢绳悬挂于跑车之下，随同跑车以v=1m/s的速度沿桥式吊车的水平桥架移动。重物之重心到悬挂点的距离为l=5m。当跑车突然停止时，重物因惯性而继续运动，此后即绕悬挂点摆动。试求钢绳的最大张力。设摆至最高位置时的偏角为8°，求此时的张力。

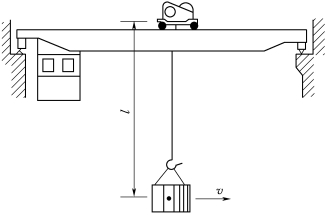
图2.101　习题1图

2.如图2.102所示，重60kN的货车以21.6km/h的速度驶入渡船。在刚驶入时开始制动，货车移动10m后停止。设货车做匀减速运动，求系渡船于岸上的绳索的拉力。假定开始刹车时绳索已拉紧。

图2.102　习题2图

3.如图2.103所示为一斜坡式升船机构。设升船车A连同船只共重W，平衡车B重Q。两车在导轨上运动时，摩擦力各为其重量的1%；导轨的倾角为α，启动时的加速度为a。试求加于鼓轮C上的力偶矩M。鼓轮的半径为r，质量不计。

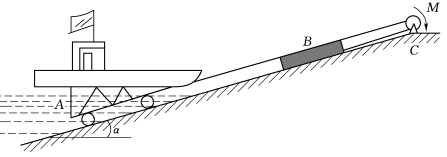
图2.103　习题3图

4.泥沙在水中下沉时，受到的阻力可用斯托克斯公式计算：F=6πηvr。其中，η为水的阻力系数；v为泥沙运动之速度，以mm/s计；r为泥沙的半径，以mm计；F以N计。已知细沙半径r=0.05mm，沙的容重γ=2.74×10-5N/mm3，η=1×10-9N·s/mm2。试求细沙在水中下沉的极限速度。