【工程实例】盐河北闸工程

盐河北闸位于江苏省灌云县侍庄乡境内的新沂河北大堤上（92.3km处），与盐河南闸共同构成了盐河穿过新沂河的航道，是集防洪、灌溉、航运于一体的综合性水利工程[图2.65（a）]。该闸始建于1970年10月，于1998年11月加固。

闸墩顶部上游侧设公路桥，桥面净宽6m，设计荷载汽-10（钢筋混凝土板梁结构）。闸墩顶部下游侧设3m宽人行便桥（钢筋混凝土现浇结构），闸墩顶部顺水流向16m长范围内布置4根撑梁（断面60cm×75cm），排架顶高17m，工作桥（钢筋混凝土预制“∏”型）桥面高程17.80m，桥面宽5.6m。闸门采用上、下扉钢结构平板门，各一台启闭机控制[图2.65（b）]。

图2.65　盐河北闸

【问题】对安装或施工期（没有水荷载）的闸门进行受力分析。

分析：取平面闸门作为研究对象，闸门承受吊杆拉力F1、F2和自重G作用，闸门受力为平面平行力系。

解：

取平面闸门作为研究对象，不考虑摩擦力，画受力图，如图2.66所示。

列平衡方程：

∑Y=0，F1+F2=G

∑MO=0，F1a1=F2a2

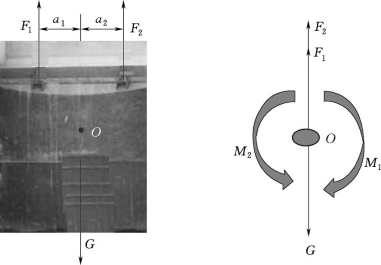
图2.66　闸门受力分析

【例题1】如图2.67所示，液压式汽车起重机全部固定部分（包括汽车自重）总重为P1=60kN，旋转部分总重为P2=20kN，a=1.4m，b=0.4m，l1=1.85m，l2=1.4m。求：

（1）当l=3m，起吊重为P=50kN时，支撑腿A、B所受地面的约束力。

（2）当l=5m时，为了保证起重机不致翻倒，问最大起重为多大？

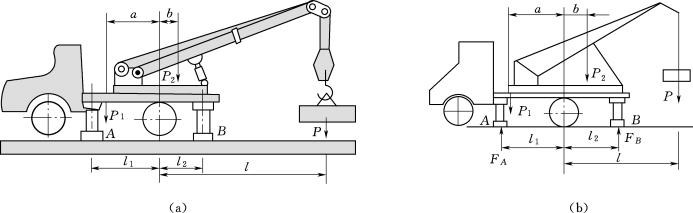
图2.67　液压式汽车起重机示意图

解：

取整体分析，坐标及受力如图2.67（b）所示。

（1）求当l=3m，P=50kN时的FA、FB。

∑MA=0，-P1（l1-a）-P2（l1+b）-P（l+l1）+FB（l1+l2）=0

∑Fy=0，FA+FB-P1-P2-P=0

FA=P1+P2+P-FB=33.2kN

（2）求当l=5m时，保证起重机不翻倒的P。起重机处于不翻倒的临界状态时，FA=0。

∑MB=0，P1（a+l2）+P2（l2-b）-P（l-l2）=0

(www.daowen.com)

由此得，Pmax=52.2kN。

【例题2】图2.68和图2.69（a）分别为一桥式起重机（通称吊车）的照片和示意图。大梁重W=180kN，小车重P=40kN，起重量Q=200kN，l=10m。求当a=2m时轨道A、B处的反力。假设小车是静止的，大梁所受的重力作用于大梁中点。

图2.68　水电站厂房桥式起重机

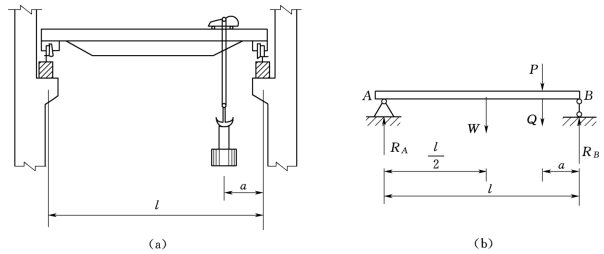
图2.69　桥式起重机示意图

解：

将轨道对于大梁的约束简化为铰支座及辊轴支座约束。作大梁的受力图如图2.69（b）所示。由于所有主动力都是铅直的，所以铰A处的反力也是铅直的。于是，W、P、Q、RA及RB组成一平衡的平行力系，由两个平衡方程可以求解RA、RB两个未知数。由

即

10RB-180×5-240×8=0

解得

RB=282kN

再由

∑Yi=0，RA+RB-W-P-Q=0

将各已知值代入，解得

RA=138kN

也可利用∑MBi=0求解出RA作为校核条件。

习题

1.如图2.70所示，行动式起重机不计平衡锤的重为P=500kN，其重心在离右轨1.5m处。起重机的起重力为P1=250kN，突臂伸出离右轨10m。跑车本身重力略去不计，欲使跑车满载时起重机均不致翻倒，求平衡锤的最小重力P2以及平衡锤到左轨的最大距离x。

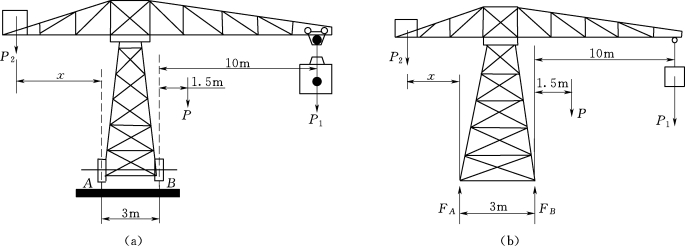
图2.70　行动式起重机示意图

2.如图2.71所示，汽车起重机在图示位置保持平衡。已知起重机质量Q=10kN，起重机自重W=70kN。求A、B两处地面的反力，起重机在这位置的最大起重重量为若干？

3.如图2.72所示，工人启闭闸门时，为了省力，常常用一根杆子插入手轮中，并在杆的一端O施力，以转动手轮。设手轮直径AB=0.6m，杆长l=1.2m，在O端用P=100N的力能将闸门开启，若不借用杆子而直接在手轮A、B处施加力偶（F，F′），问F至少应为多大才能开启闸门？

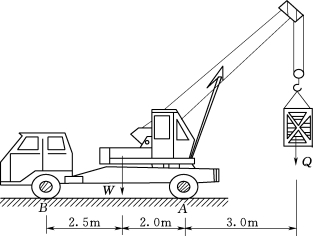
图2.71

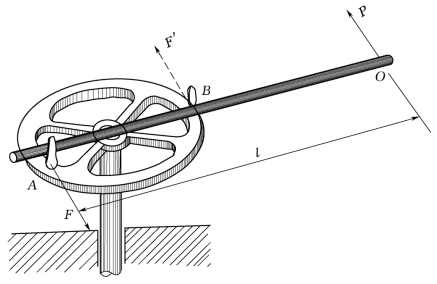
图2.72　闸门手轮示意图