【问题】对起吊安装（图2.47）时的平面闸门进行受力分析和求解。

图2.47　节制闸工程闸门安装

分析：取平面闸门作为研究对象，闸门受力为平面汇交力系。

解：

取平面闸门作为研究对象，闸门受到绳子的拉力F1、F2和自重G的作用保持平衡，假定F1、F2与竖直方向的夹角为α1、α2，不考虑摩擦力，画受力图，如图2.48所示。

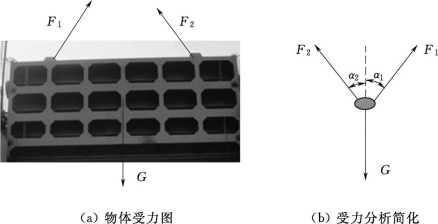
图2.48　闸门起吊受力分析

列平衡方程：

∑X=0，F1sinα1=F2sinα2

∑Y=0，F1cosα1+F2cosα2=G

【例题】如图2.49（a）所示的压路碾子，自重P=20kN，半径R=0.6m，障碍物高h=0.08m。碾子中心O处作用一水平拉力F。求：

（1）当水平拉力F=5kN时，碾子对地面及障碍物的压力。

（2）欲将碾子拉过障碍物，水平拉力至少应为多大。

（3）F沿什么方向拉动碾子最省力，此时F为多大。

图2.49　压路碾子示意图

解：

（1）选碾子为研究对性，其受力图如图2.49（b）所示，各力组成平面汇交力系。根据平衡的几何条件，力P、F、FA与FB应组成封闭的力多边形。按比例先画已知力矢P与F如图2.49（c）所示，再从a、c两点分别作平行于FB、FA的平行线，相交于点d。将各力矢首尾相接，组成封闭的力多边形，则图2.49（c）中的矢量即为A、B两点约束反力FA、FB的大小与方向，按比例量得

FA=11.4kN，FB=10kN

由图2.49（c）的几何关系，也可以计算FA、FB的数值。按已知条件可求得

(www.daowen.com)

α=30°

再由图2.49（c）中各矢量的几何关系，可得

FBsinα=F

FA+FBcosα=P

解得

FA=P-FBcosα=11.34kN

根据作用与反作用关系，碾子对地面及障碍物的压力分别等于11.34kN和10kN。

（2）碾子能越过障碍物的力学条件是FA=0，因此，碾子刚刚离开地面时，其封闭的力三角形如图2.49（d）所示。由几何关系，此时水平拉力

F=Ptanα=11.55kN

此时B处的约束反力

（3）从图2.49（d）中可以清楚地看到，当拉力与FB垂直时，拉动碾子的力最小，即

Fmin=Psinα=10kN

习题

1.如图2.50所示为一履带式起重机，起吊重量P=100kN，在图示位置平衡。如不计吊臂AB自重及滑轮半径和摩擦，求吊臂AB及缆绳AC所受的力。

2.如图2.51所示，弧形闸门自重W=150kN，试用作图法求提起闸门所需的拉力T和铰支座A处的反力。

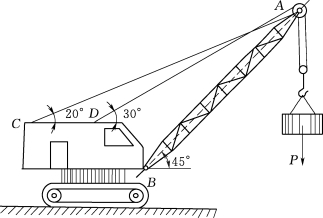
图2.50　履带式起重机图

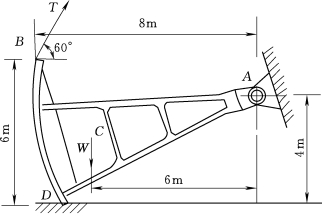
图2.51　弧形闸门结构图