Vapnik提出的支持向量机（Support Vector Machine，SVM）以训练误差作为优化问题的约束条件，以置信范围值最小化作为优化目标，即SVM是借助于最优化方法解决机器学习的问题的新工具，是一种基于结构风险最小化准则的学习方法，在解决小样本、非线性和高维模式识别问题中有较大优势，并能够推广应用到函数拟合等其他机器学习问题中，其推广能力明显优于一些传统的学习方法。

支持向量机是使用训练实例的一个子集来表示决策边界，这个子集称为支持向量。

图6-17给定一个数据集，包含属于两个不同类的样本，分别用方块和圆圈表示。能否找到这样一个线性超平面（决策边界），使得所有的方块位于这个超平面的一侧，而所有的圆圈位于它的另一侧？

SVM考虑寻找一个满足分类要求的超平面，并且使训练集中的点距离分类面尽可能地远，也就是寻找一个分类面使它两侧的空白区域最大。两类样本中离分类面最近的点且平行于最优分类面的2个超平面上的训练样本就称作支持向量。

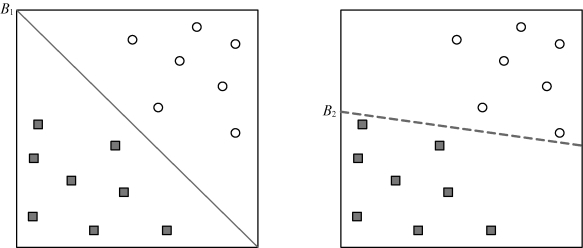
图6-18中决策边界B1和B2都可以使得方块和圆圈分开，哪一个更好一些通常引入泛化误差来比较。

图6-17　线性可分数据集

(www.daowen.com)

图6-18　线性可分数据集两种决策边界

具有较大边缘的决策边界比那些具有较小边缘的决策边界具有更好的泛化误差。直觉上，如果边缘比较小，界上任何轻微的扰动都可能对分类产生显著的影响。因此，那些决策边界较小的分类器对模型的拟合更加敏感，从而在未知的样本上泛化能力很差。

统计学理论给出了线性分类器边缘与其泛化误差之间关系的形式化解释，这种理论称为结构风险最小化理论。

结构风险最小化理论明确地给出，在概率1－η的情况下，分类器的泛化误差在最坏的情况下满足：

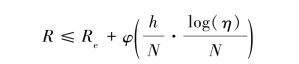
然而，依据结构风险最小化理论，随着能力的增加，泛化误差的上界也随之增加。因此，需要设计最大化决策边界的边缘的线性分类器，以确保最坏情况下的泛化误差最小。

线性模型的能力与它的边缘逆相关。即具有较小边缘的模型具有较高的能力，因为与具有较大边缘的模型不同，具有较小边缘的模型更灵活，能拟合更多的训练集。线性SVM就是这样的分类器。