对不完备信息的研究主要考虑三种关系:容差关系(tolerance relation)、非对称相似关系(non symmetric similarity relation)和量化容差关系(valued tolerance relation)。
设S=(U,A)是一个信息系统,其中U是对象的非空有限集合,A是属性的非空有限集合。对于每一个a∈A,用Va表示属性a的值集。
每一个属性子集P⊆A决定了一个二元不可区分关系IND(P):
显然,IND(P)是集合U上的一个等价关系。
如果对于至少一个属性a∈A,Va包括空值,则称S是一个不完备信息系统,否则它是完备的。
一个信息系统中的数据基本反映了它所涉及的问题(或领域)的基本特征,尽管系统中可能存在遗失的数据。不完备信息系统中的遗失数据值的填补,应该尽可能反映此信息系统所反映的基本特征以及隐含的内在规律。填补的目标是使具有遗失值的对象与信息系统的其他相似对象的属性值尽可能保持一致,使属性值之间的差异尽可能保持最小。
1)可辨识矩阵
可辨识矩阵(也称分明矩阵),是由斯科龙(Skowron)教授提出的。
定义6.8:令决策表系统为S=<U,R,V,f>,R=P∪D是属性集合,子集P={ai|i=1,…,m}和D={d}分别称为条件属性和决策属性集,U={x1,x2,…,xn}是论域,ai(xj)是样本xj在属性ai上的取值。CD(I,j)表示可辨识矩阵中第I行j列的元素,则可辨识矩阵CD定义为
其中,i,j=1,…,n。
根据可辨识矩阵的定义可知,当两个样本(实例)的决策属性取值相同时,它们所对应的可辨识矩阵元素的取值为0;当两个样本的决策属性不同且可以通过某些条件属性的取值不同加以区分时,它们所对应的可辨识矩阵元素的取值为这两个样本属性值不同的条件属性集合,即可以区分这两个样本的条件属性集合;当两个样本发生冲突时,即所有的条件属性取值相同而决策属性的取值不同时,则它们所对应的可辨识矩阵中的元素取值为空集。显然,可辨识矩阵元素中是否包含空集元素可以作为判定决策表系统中是否包含不一致(冲突)信息的依据。
定义6.9:令信息系统为S=<U,R,V,f>,A={ai|i=1,…,m}是属性集,U={x1,x2,…,xn}是论域,ai(xj)是样本xj在属性ai上的取值。M(i,j)表示经过扩充的可辨识矩阵中第i行j列的元素,则经过扩充的可辨识矩阵M定义为
其中,i,j=1,…,n;*表示遗失值
定义6.10:令信息系统为S=<U,R,V,f>,A={ai|i=1,…,m}是属性集,设xi∈U,则对象遗失属性集MAS对象xi的无差别对象集NSi和信息系统S的遗失对象集MOS分别定义为
设初始信息系统为S0,对象集为{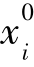 },相应的扩充可辨识矩阵为M0,xi的遗失属性集为
},相应的扩充可辨识矩阵为M0,xi的遗失属性集为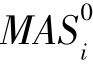 ,无差别对象集为
,无差别对象集为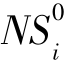 ;第r次完整化分析后的信息系统为Sr,对象集为{xir},相应的扩充可辨识矩阵为Mr,xi的遗失属性集为
;第r次完整化分析后的信息系统为Sr,对象集为{xir},相应的扩充可辨识矩阵为Mr,xi的遗失属性集为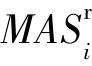 ,无差别对象集为
,无差别对象集为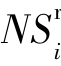 。
。
定理6.1:设Mr+1=(Mr+1(i,j))n×n,r=0,1,2,…,则Mr+1(i,j)计算如下:
由此定理,当计算好初始的扩充可辨识矩阵后,在计算新的信息系统所对应的扩充可辨识矩阵时,不必重新计算,而只需计算上次可辨识矩阵中由于遗失值的填补而引起的局部元素值的修改,从而大大简化了计算复杂性。(www.daowen.com)
2)基于Rough集理论的不完备数据分析方法(ROUSTIDA)
输入:不完备信息系统S0=<U0,R,V,f0>;
输出:完备的信息系统Sr=<Ur,R,V,fr>;
步骤1:计算初始可辨识矩阵M0,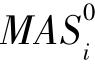 和MOS0;令r=0;
和MOS0;令r=0;
步骤2:
①对于所有i∈MOSr,计算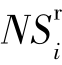 ;
;
②产生Sr+1
对于,k=1,2,…,m;
对于所有i∈MOSr,对所有k∈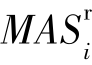 作循环:
作循环:
①如果![]() ,设j∈
,设j∈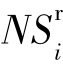 ,若
,若![]() ,则
,则![]() 否则
否则![]()
②否则,
(ⅰ)如存在j0 和![]() ,满足
,满足
如果Sr+1=Sr,结束循环转步骤3。
否则,计算Mr+1,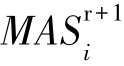 和MOSr+1;r=r+1;转步骤2。
和MOSr+1;r=r+1;转步骤2。
步骤3:如果信息系统还有遗失值,可用取属性值中平均值(数字型)或出现频率最高的值(符号型)的方法处理(当然,也可用其他方法);
步骤4:结束
粗糙集(Rough Set)理论是由波兰华沙理工大学Pawlak教授于20世纪80年代初提出的一种研究不完整、不确定知识和数据的表达、学习、归纳的理论方法,其主要思想是在保持分类能力不变的前提下,通过知识约简,导出问题的决策或分类规则。目前,粗糙集理论已经在机器学习、决策分析、过程控制、模式识别与数据挖掘等方面得到了较为成功的应用。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。







