1.基本运算过程

依标准形式，它使用二进制遗传编码，即等位基因Г=｛0，1｝，个体空间HL=｛0，1｝L，且繁殖分为交叉与变异两个独立的步骤进行。遗传算法的基本运算过程如下：

步骤1（初始化）　确定种群规模N，交叉概率Pc，变异概率Pm和置终止进化准则；随机生成N个个体作为初始种群X→（0）；置t←0。

步骤2（个体评价）　计算或估价X→（t）中各个体的适应度。

步骤3（种群进化）：

3.1　选择（母体）　从X→（t）中运用选择算子选择出M/2对母体（M≥N）。

3.2　交叉　对所选择的M/2对母体，依概率Pc执行交叉，形成M个中间个体。

3.3　变异　对M个中间个体分别独立依概率Pm执行变异，形成M个候选个体。

3.4　选择（子代）　从上述所形成的M个候选个体中依适应度选择出N个个体组成新一代种群X→（t+1）。

步骤4（终止检验）　如已满足终止准则，则输出X→（t+1）中具有最大适应度的个体作为最优解，终止计算，否则置t←t+1并转步骤3。

此算法为最基本的遗传算法思想，对它还有各种推广与变形。

简单地说，遗传算法的基本步骤就是对一个种群中的染色体，重复地做繁殖、交叉、变异操作；计算适应度；并按适应度进行选择，直至达到目标。

2.工作步骤

对实际问题实施遗传算法通常需要如下步骤：

（1）对实际问题进行编码，随机建立由字符串组成的初始群体。（2）计算群体中各个体的适应度。

（3）根据交叉、变异概率，进行以下操作产生新的群体：

a.繁殖。通过计算选择出优良个体复制后加入新的群体中，删除不良个体；

b.交叉。根据交叉概率选择出两个个体进行交换，所产生的新个体加入新的群体中；　

c.变异。根据变异概率，改变某一个体的某个字符后，所产生的新个体加入新的群体中。

4.反复执行（2）（3），一旦达到终止条件，选择最佳个体作为实施遗传算法的结果，即得到最优解。

对于算法何时停止，终止条件有如下设定方法：

①规定遗传迭代的次数，如100次或1 000次，根据情况选择。

②根据目标函数值和实际目标值之差小于某一允许值，则停止。

③一旦最优个体的适应度不再变化或变化很小时，算法终止。

在用遗传算法实际解决问题时，以下问题是非常关键的：种群规模的确定，编码的方式选择和长度的设定、适应度函数的选择与计算、繁殖、交叉、变异算子等参数的选择。对这些问题我们还可进一步进行深入讨论与研究，合适参数的选定，将对整个算法起到优化作用。现有的一些方法已有广泛地使用，可参考相关文献，在此不再详述。

下面用一个简单的例子来说明遗传算法思想及一般处理过程。

例：设函数f（x）=x2，求其在区间x∈［0，31］内的最大值。

1）编码。

用字符串（相当于染色体）编码。用5位二进制对x进行编码。

初始群体采用随机的方法产生，假设为：01101，11000，01000，10011，对应的x为13，24，

8，19。

2）计算适应度。(www.daowen.com)

在本例中，用f（xi）表示第i个染色体的适应度值，f（xi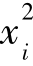）=，对每个染色体计算出适应度；

同时，作如下符号约定，并相应计算：

①xi为种群中第i个染色体；

②f（xi）为第i个染色体的适应度值，f（xi）=；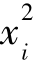

③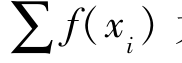为种群中所有染色体的适应度值之和；

④f（xi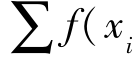）／）为某染色体被选的概率；

⑤f 为适应度的平均值，由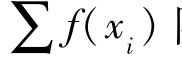除以种群个数得出；

⑥f（xi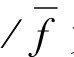）为每个个体的相对适应度，反映个体之间的相对优劣性。

⑦Mp表示传递给下一代的个体数目（复制的个体Mp=2，淘汰的个体Mp=0，其他的个体Mp=1）。

通过计算得到：个体编号为2的个体适应度f（xi ）为576，在所有个体中最高，并且被选的概率f（xi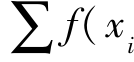）／）最高，为0.49，其相对适应度f（xi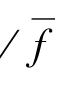为1.97，也是最高的一个，在所有个体中是优良个体。而个体编号为3的个体相对适应度f（xi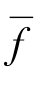）为0.22，为不良个体。

3）繁殖。

将现有群体变为下一代群体的方法是从旧群体中选择优良个体进行复制。在本例中我们根据个体相对适应度f（xi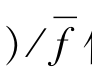作为复制的依据，适应度大的个体接受复制，使之繁殖；适应度小的个体则淘汰，进行删除，使之死亡。

根据计算我们得到，个体编号为2的个体性能最优，接受复制，进行繁殖；个体编号为3的个体性能最差，将其删除，使之死亡；个体编号为1，4的个体处于中间地位，原样传递到下一代。

用Mp表示了传递给下一代的个体数目，则个体编号为2的个体Mp=2，个体编号为3的个体Mp=0，其他的个体Mp=1。

表6-1给出了初始种群和相应的参数值。

表6-1　第0代种群

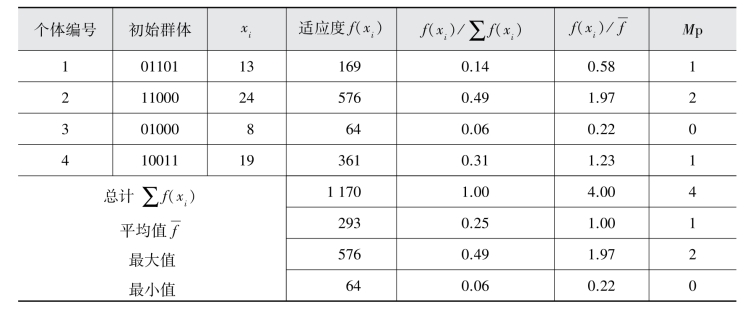
经过以上步骤，产生了下一代新的群体（第1代种群）：01101、11000、11000、10011，对应的x为13，24，24，19。其中，第3个个体是由第2个个体复制得来，原来的第3个个体已经被淘汰。对它们以同样的方法计算适应度（见表6-2）。

表6-2　第1代种群

4）交叉。

通过复制产生的新群体，其性能得到了改善，但是它不能产生新的个体。为了产生新个体，对染色体的某些部分进行交叉换位。进行交换的母体都选自经过复制产生的新一代个体。

在本例中，利用随机配对的方法，选定个体编号1，2的进行交换，个体编号3，4的进行交换。（在表6-2交换对象列给出）。

交换的位置采用随机定位的方法，确定个体编号1，2的进行交换的位置是4，即互换从字符串左数第4位开始起到末尾的部分字符串。（在表6-2交换位置列给出）。交换前的群体为：01101、11000，字符串左数第4位开始的字符串以划线作为标识，即两个个体交换划线部分字符串，得到交换后的群体为：01100、11001。

个体编号3，4的进行交换的位置是3，即互换从字符串左数第3位开始起到末尾的部分字符串。交换前的群体为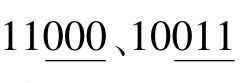：，得到交换后的群体为：11011、10000。

计算出交换后的个体适应度f（xi）。（见表62最后列）。

从表6-2可以看出，个体编号为3的个体，在交换后适应度为729，大大高于交换前的适应度526。同时，交换后平均值也由421提高到439，这就说明了，交换后的群体朝着优良方向发展。

5）变异。

根据变异概率将个体字符串某位符号进行逆变：1变为0，或0变为1。

个体是否进行变异以及在哪个部位变异，由事先给定的概率决定，也可随机进行。通常，变异的概率很小，约为0.001～0.10。

在此例中，随机选择个体编号为4的个体，对第3位进行变异，原个体为：10000，新个体为：10010。

将上述（2）～（5）反复执行，直至得到最优解。