不同的学习框架下建立的学习模型不同.例如，卷积神经网络（Convolutional neural networks，CNNs）是一种深度的监督学习下的机器学习模型，而深度置信网（Deep Belief Nets，DBNs）是一种无监督学习下的机器学习模型（见图6-10）。

从一个输入中产生一个输出所涉及的计算可以通过一个流向图（flow graph）表示：流向图是一种能够表示计算的图，在这种图中每一个节点表示一个基本的计算以及一个计算的值，计算的结果被应用到这个节点的子节点的值。考虑这样一个计算集合，它可以被允许在每一个节点和可能的图结构中，并定义了一个函数族。输入节点没有父节点，输出节点没有子节点。

这种流向图的一个特别属性是深度（depth）：从一个输入到一个输出的最长路径的长度。

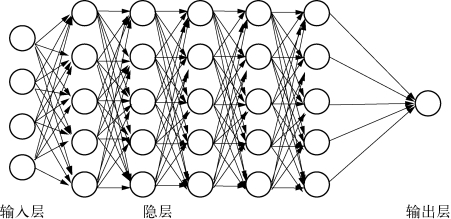
图6-10　深度学习模型

1.deep learning训练过程

（1）使用自底向上的非监督学习。

分层训练各层参数，是一个无监督训练过程。首先用无决策属性的数据训练第一层，训练时先学习第一层的参数（这一层可以看作是得到一个使得输出和输入差别最小的神经网络的隐层），由于模型容量的限制以及稀疏性约束，使得得到的模型能够学习到数据本身的结构，从而得到比输入更具有表示能力的特征；在学习得到第n－1层后，将n－1层的输出作为第n层的输入，训练第n层，由此分别得到各层的参数；

（2）自顶向下的监督学习（就是通过带决策属性的数据去训练，误差自顶向下传输，对网络进行微调）。

基于第一步得到的各层参数进一步调节整个多层模型的参数，这一步是一个有监督训练过程；第一步类似神经网络的随机初始化初值过程，由于深度学习的第一步不是随机初始化，而是通过学习输入数据的结构得到的，因而这个初值更接近全局最优，从而能够取得更好的效果；所以深度学习效果好很大程度上归功于第一步的无监督学习过程。

2.深度学习的常用模型

1）自动编码器

自动编码器AutoEncoder是一种用于训练相邻两层网络模型的一种方法。是典型的无监督学习算法，其结构如图6-11所示。

图中，最左侧是输入层，中间是隐含层，最右边是输出层。对于输入X，假设输入X=（x1，x2，…，xd），且xi∈［0，1］，自编码器首先将输入X映射到一个隐含层，利用隐含层对其进行表示为H=（h1，h2，…，hd），且hi∈［0，1］，这个过程被称为编码（Encode），隐含层的输出H的具体形式为：H=σ（W1X+b1）。其中，σ为一个非线性映射，如Sigmoid函数。

隐含层的输出H被称为隐含的变量，利用该隐含的变量重构Z。这里输出层的输出Z与输入层的输入X具有相同的结构，这个过程被称为解码（Decode）。输出层的输出Z的具体形式为：Z=σ（W2H+b2）。

输出层的输出Z可以看成是利用特征H对原始数据X的预测。

图6-11　AutoEncoder的结构

从上述的过程中可以看出，解码的过程是编码过程的逆过程，对于解码过程中的权重矩阵W2可以被看成是编码过程的逆过程，即W2=W1T。

为了使得重构后Z和原始的数据X之间的重构误差最小，首先需要定义重构误差，定义重构误差的方法有很多种，如使用均方误差，1=‖X－Z‖2。或者使用交叉熵作为其重构误差：

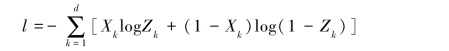
【黄安埠】隐含层的设计有两种方式：①隐藏层神经元个数小于输入层神经元个数，称为undercomplete。使得输入层到隐藏层的变化本质上是一种降维操作，网络试图以更小的维度去描述原始数据而尽量不损失数据信息，从而得到输入层的压缩表示。②隐藏层神经元个数大于输入层神经元个数，称为overcomplete。该隐藏层设计一般用于稀疏编码器，可以获得稀疏的特征表示，也就是隐藏层中有大量的神经元取值为零。

2）稀疏自动编码器

在AutoEncoder的基础上加上L1的Regularity限制（L1主要是约束每一层中的节点中大部分都要为0，只有少数不为0），得到稀疏自动编码器法。

限制每次得到的表达编码尽量稀疏，因为稀疏的表达往往比其他的表达要有效。

3）降噪自动编码器

目前数据受到噪声影响时，可能会使获得的输入数据本身就不服从原始的分布。在这种情况下，利用自编码器，得到的那个结果也将是不正确的，为了解决这种由于噪声产生的数据偏差问题，提出了DAE网络结构在输入层、隐藏层之间添加了噪声处理，噪声层处理后得到新的数据，然后按照这个新的噪声数据进行常规自编码器变换操作。

4）受限波尔兹曼机（RBM）

假设有一个二部图，每一层的节点之间没有链接，一层是可视层，即输入数据层（v），一层是隐藏层（h），如果假设所有的节点都是随机二值变量节点（只能取0或者1值），同时假设全概率分布p（v，h）满足Boltzmann分布，这个模型称受限波尔兹曼机（RBM）（见图6-12）。(www.daowen.com)

这个模型是二部图，所以在已知v的情况下，所有的隐藏节点之间是条件独立的（因为节点之间不存在连接），即p（h|v）=p（h1|v）…p（hn|v）。同理，在已知隐藏层h的情况下，所有的可视节点都是条件独立的。同时又由于所有的v和h满足Boltzmann分布，因此，当输入v的时候，通过p（h|v）可以得到隐藏层h，而得到隐藏层h之后，通过p（v|h）又能得到可视层，通过调整参数，从隐藏层得到的可视层v1与原来的可视层v如果一样，那么得到的隐藏层就是可视层另外一种表达，因此隐藏层可以作为可视层输入数据的特征，所以它就是一种深度学习方法。

联合组态的能量表示为：

图6-12　受限波尔兹曼机

而某个组态的联合概率分布可以通过Boltzmann分布和组态的能量确定：

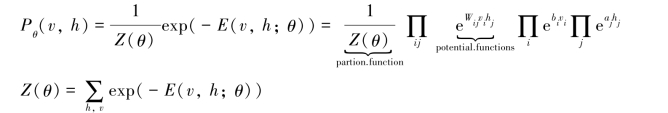
因为隐藏节点之间是条件独立的（因为节点之间不存在连接），即

然后可以比较容易（对上式进行因子分解Factorizes）得到在给定可视层v的基础上，隐层第j个节点为1或者为0的概率：

同理，在给定隐层h的基础上，可视层第i个节点为1或者为0的概率也可以容易得到：

给定一个满足独立同分布的样本集：D=｛v（1），v（2），…，v（N）｝，需要学习参数θ=｛W，a，b｝。

对数似然函数（最大似然估计：对于某个概率模型，需要选择一个参数，让当前的观测样本的概率最大）最大化：

也就是对最大对数似然函数求导，就可以得到L最大时对应的参数W了。

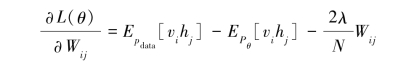
如果把隐藏层的层数增加，可以得到深度波尔兹曼机（DBM）；如果我们在靠近可视层的部分使用贝叶斯信念网络（即有向图模型，当然这里依然限制层中节点之间没有链接），而在最远离可视层的部分使用受限玻尔兹曼机，我们可以得到深度信念网络（DBN）。

5）卷积神经网络（CNN）

为了能够减少参数的个数，卷积神经网络中提出了三个重要的概念：①稀疏连接；②共享权值；③池化。其中稀疏连接主要是通过对数据中局部区域进行建模，以发现局部的一些特性。共享权值的目的是为了简化计算的过程，使得需要优化的参数变少；自采样的目的是解决图像中的平移不变性及所要识别的内容与其在图像中的具体位置无关。池化是卷积神经网络中一个比较重要的概念，一般可以采用最大池化。在最大池化中将输入图像划分成为一系列不重叠的正方形区域，然后对于每一个子区域输出其中的最大值。

在卷积神经网络中最重要的是卷积层、下采样层和全连接层，这3层分别对应的卷积神经网络中最重要的三个操作，卷积操作、最大池化操作和全连接的MLP操作。

卷积神经网络是深度学习技术中极具代表性的网络结构，它的应用非常广泛，尤其是在计算机视觉领域取得了很大的成功。相较于传统的图像处理算法的优点在于一年来对图像复杂的前期预处理过程及大量的人工提取特征工作，能够直接从原始像素出发，经过极少的预处理就能够识别出视觉上的规律，但受到当时环境的制约，计算机的计算能力跟不上，使得深度学习依赖的两大基础因素燃料和引擎都没有得到很好的满足。2006年起，在大数据和高性能计算平台的推动下，数学家们开始重新改造卷积神经网络，并设法克服难以训练的困难，其中最著名的是AlexNet，该网络结构在图像识别任务上取得了重大突破，并以创纪录的成绩夺得当年的ImageNet冠军。卷积神经网络的变种网络结构，还包括：ZFNet、VGGNet、GoogleNet和ResNet4种。从结构看，卷积神经网络发展的一个显著特点就是层数变得越来越深，结构也变得越来越复杂，通过增加深度，网络能够呈现出更深层、更抽象的特征。

传统的神经网络处理是一个全连接的网络，是在输入层接收原始数据，然后把数据传送到隐藏层，并不断向后抽象。但全联接的深度网络存在很多缺点，如梯度消失、局部最优解、可扩展性差等。卷积神经网络的设计做了相应的改进，并且避免了对输入数据复杂的预处理，实现了端到端的表示学习思想。卷积运算是定义在两个连续失值函数上的数学操作。卷积网络在进入全连接层之前已经经过了多个卷积层和池化层的处理。

卷积层：卷积神经网络的核心结构，通过局部感知和参数共享两个原理，实现了对高维输入数据的降维处理，并且能够自动提取原始数据的优秀特征。

激活层：它的作用与传统深度神经网络的激活层一样，把上一层的线性输出通过非线性的激活函数进行处理。

池化层：也称为子采样层或下采样层，是卷积神经网络的另一个核心结构通过层。通过对输入数据的各个维度进行空间的采样，可以进一步降低数据规模，并且对输入数据具有局部线性转换的不变性，增强网络的泛化处理能力。

全连接层：等价于传统的多层感知机MLP，经过前面的卷积层和池化层的反复处理后，一方面输入数据的维度已经下降至可以直接采用前馈网络来处理；另一方面，全连接层的输入特征是经过反复提炼的结果，因此比直接采用原始数据作为输入所取得的效果更好。

卷积神经网络已成为当前语音分析和图像识别领域的研究热点。它的权值共享网络结构使之更类似于生物神经网络，降低了网络模型的复杂度，减少了权值的数量。在网络的输入是多维图像时表现得更为明显，使图像可以直接作为网络的输入，避免了传统识别算法中复杂的特征提取和数据重建过程。卷积网络是为识别二维形状而特殊设计的一个多层感知器，这种网络结构对平移、比例缩放、倾斜或者其他形式的变形具有高度不变性。