［例］　积木世界的机器人问题（见图3-4）。

设有个积木世界和一个机器人。积木世界是几个有标记的立方形积木（假定大小一致），它们或者互相堆叠在一起，或者摆在桌面上。机器人有个可移动的机械手，它可以抓起积木块并移动积木从一处至另一处。如何规划机器人的动作序列，使得问题从初始状态到达目标状态？

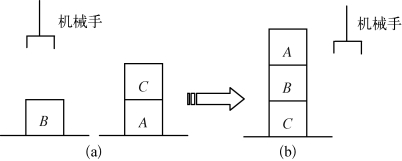
图3-4　积木世界

（a）初始状态　（b）目标状态

机器人问题的状态描述和目标描述可用下列谓词描述：

ON（A，B）：积木A在积木B之上。

ONTABLE（A）：积木A在桌面上。

CLEAR（A）：积木A顶上没有任何东西。

HOLDING（A）：机械手正抓住积木A。

HANDEMPTY：机械手为空手。

初始状态为：

CLEAR（B）：积木B顶上没有任何东西。

CLEAR（C）：积木C顶上没有任何东西。

ON（C，A）：积木C在积木A之上。

ONTABLE（A）：积木A在桌面上。

ONTABLE（B）：积木B在桌面上。

HANDEMPTY：机械手为空手。

目标状态：

ON（B，C）∧ON（A，B）

采用正向推理规则（forward chaining）F规则来规划机器人的动作序列，这是SPRIPS（Stanford Research Institute Problem Solver，斯坦福研究所问题求解系统）规划系统的规则。

这个正向推理规则由三部分组成.第一部分是先决条件。这个先决条件公式必须是逻辑上遵循状态描述中事实的谓词演算表达式。在应用规则之间必须确信先决条件是真的。第二部分是一个叫作删除表的谓词。当一条规则被应用于某个状态描述或数据库时，就从该数据库删去删除表的内容。第三部分称为添加表。当把某条规则应用于某数据库时，就把该添加表的内容添进该数据库。

积木世界中move这个动作可以表示如下：

move（x，y，z）：把物体x从物体y上面移到物体z上面。

先决条件：CLEAR（x），CLEAR（z），ON（x，y）

删除表：ON（x，z），CLEAR（z）

添加表：ON（x，z），CLEAR（y）

如果move为此机器人仅有的操作符或适用动作，那么可以生成如图3-5所示的搜索图或搜索树。(www.daowen.com)

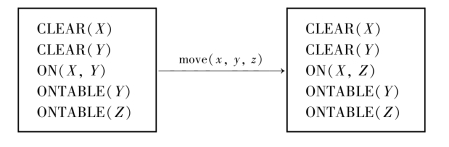
图3-5　表示move动作的搜索树

对于积木世界机器人的4个动作（操作）可用SPRIPS形式表示如下：

1）stcak（X，Y）

先决条件和删除表：HOLDING（X）∧CLEAR（Y）

添加表：HANDEMPTY，ON（X，Y）

2）unstack（X，Y）

先决条件：HANDEMPTY∧ON（X，Y）∧CLEAR（X）

删除表：ON（X，Y），HANDEMPTY

添加表：HOLDING（X），CLEAR（Y）

3）pickup（X）

先决条件：ONTABLE（X）∧CLEAR（X）∧HANDEMPTY

删除表：ONTABLE（X）∧HANDEMPTY

添加表：HOLDING（X）

4）putdown（X）

先决条件和删除表：HOLDING（X）

添加表：ONTABLE（X），HANDEMPTY

图3-6给出了积木世界的全部状态空间，并用粗线指出了从初始状态S0到目标状态G的解答路径。在这个状态空间图中，初始节点没有放在图的顶点上，而且每条规则都有一条逆规则。

沿着粗线所示的线路，从初始状态开始，依次正向地读出连接弧上的F规则，得到一个能达到目标状态的动作序列：｛unstack（C，A），putdown（C），pickup（B），stcak（B，C），pickup（A），stcak（A，B）｝

把这个动作序列称为达到这个积木世界机器人问题目标的规划。

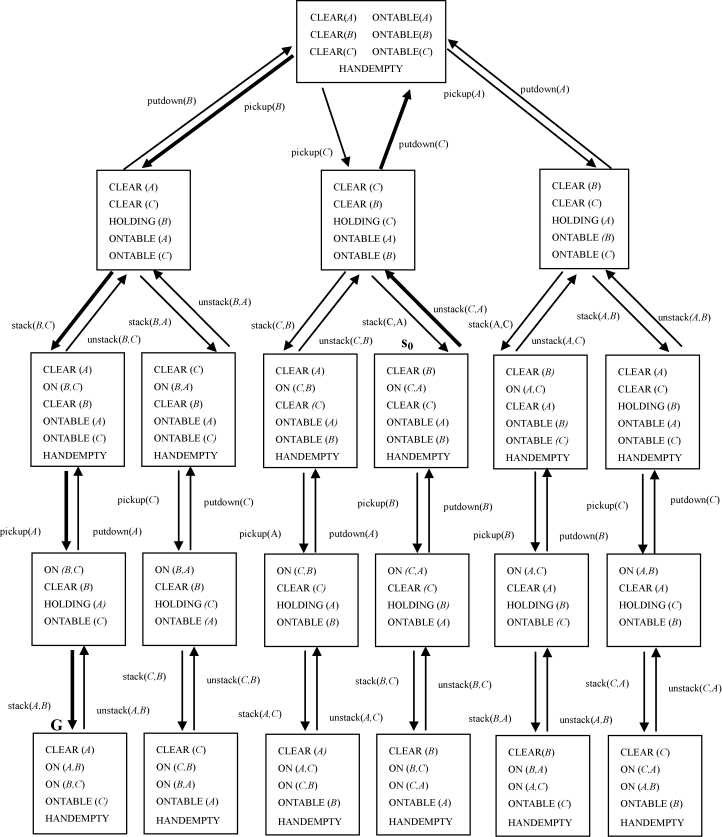
图3-6　积木世界机器人问题状态空间

习题

（1）试述机器规划的含义、意义及规划策略。

（2）用本章讲过的方法解决如图3-7所示的机器人垒积木问题，给出所生成的动作规划。

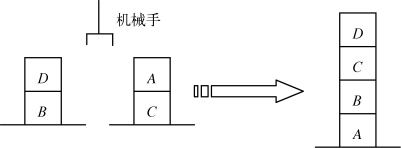
图3-7　机器人垒积木问题