1）规划问题求解

包括解路径和解结果两个方面。

注意：最佳解路径和最佳解结果是相互唯一对应的，知其一就可得到另一个。

若最佳解路径是所有解路径中深度最小的，则对应于操作序列所使用的策略集是最精练的，即数量上是最少的。

2）最优规划原理

设D0为总规划策略集，SP为规划最佳解路径上任一中间节点，DP为已使用的策略集，S为规划的初态集，G为目标集，则最优规划原理可叙述为：若DP为最优规划策略集，则余下的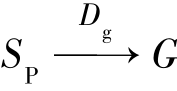策略子集Dg=（Do－DP）也必是最优的。证明：

已知SP为规划最佳解路径上任一中间节点，由最优规划策略集取得最小值的前提得：　

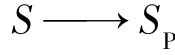若已使用的不一定是最优的，则必定存在一个对应最佳路径的最优策略子集D′P，且有D′P≤DP(www.daowen.com)

若设Dg不一定是最优的，则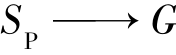也必定存在一个最优策略子集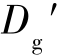，于是有

而由已知：Dg=D0－DP≤D0－=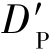

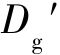
得到：Dg≤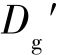

这与Dg不为最优子集的假设矛盾，故只可能Dg=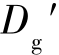为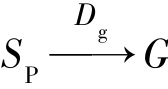对应于最佳解路径的最优策略子集。

3）条件局部最优问题

DP也必定是　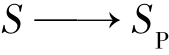的最优策略子集。

在规划求解中，若有些子问题已有成熟解法或已为本原问题，则更有利于加快搜索求解过程。例如：已知用1艘船可分别解决2传教士与2野人或3传教士与3野人的规划过河问题。若需用2艘船解决4传教士与4野人或6传教士与6野人的过河问题，就可采用分解规划策略。两船同步行动，则该问题即可利用已有解的本原子问题快速得解。