一个推理规则实际上是一个从其他谓词演算命题产生新的谓词演算命题的机械化方法。关于推理规则，有如下定义：

定义1：满足、模型、有效、不一致

对于一个谓词演算表达式S和一个解释I：

如果S在解释I下为T，则S称为得到了满足；

如果对于I（x）的所有变元指派，I均能使S满足，则称I为S的一个模型；

S可满足当且仅当存在一个解释和一个变元指派使S满足，否则称S是不可满足的；

一个表达式集是可满足的，当且仅当存在一个解释和变元指派，使它的每个元素都满足；

如果一组表达式是不可满足的，则称它们是不一致的；

如果S对于所有的解释，其真值都为T，则称S是有效的。

［例1］　S：∀X（human（X）→Mortal（X））

I：human（socrates）

X：mortal（socrates）

S是可满足的，也是有效的，I为S的一个模型。

［例2］　∃X（P（X）∧¬P（X））是不一致的。

∀X（P（X）∨¬P（X））是有效的。

注：真值表可以用于验证不包含变元的任何表达式的有效性，对有变元的表达式必须要用证明过程。

定义2：证明过程

一个证明过程是一个推理规则和用于产生一组逻辑表达式的新命题的算法的结合。定义3：逻辑结果、合理性和完备性

如果所有使谓词演算表达集S满足的解释与变元指派也使谓词演算表达式X得到满足，则称X是S的逻辑结果。

如果用一个推理规则从谓词演算表达式集合S产生的每个谓词演算表达式是S的逻辑结果，则称这个推理规则是合理的。

如果同一个推理规则可以产生给定的谓词演算表达式集合S的所有逻辑结果，则称该推理规则是完备的。

如图2-40所示的假言推理是一个合理的推理规则。

图2-40　假言推理

定义4：假言推理，取拒式，消除规则，引入规则，全称代入规则

如果P，P→Q为真，它用假言推理得出Q为真。

如果P→Q为真，且Q为假，则用取拒式得出¬P为真。

应用消除规则，我们可以从一个为真的合取式推出其中的合取项为真。例如：P∧Q为真，则P和Q都为真。

应用引入规则，可以从合取项都为真推出合取式为真。例如：如果P，Q为真，则P∧Q也为真。(www.daowen.com)

应用全称代入，当命题中的全称性变元由其变域中的项代入后命题仍为真，∀X P（X），我们在X的值域内能够得出P（a）。

［例3］　假言推理实例

｛“如果天在下雨，则地将会湿”以及“天正在下雨”｝

若地的确是湿的，则真值表为｛P→Q，P，Q｝

1.置换

定义：置换是形如｛t1/a1，t2/a2，…，tn/an｝的有限集合，其中t1，t2，…，tn与a1，a2，…，an是互不相同的项（项可以是变量符号，常数符号，或函数表达式）

注：t1/a1表示用t1代替a1

注：置换交换律不成立。常元可代换变元，常元不能换常元。两个不同常元不能代入同一变元中，一个变元不能与包含该变元的项代换。

2.合一

1）相关定义

定义1：设有一组公式F=｛F1，F2，…，Fn｝，若有一个置换Q，使得F1Q=F2Q=…=FnQ，则称Q为F的一个合一。

［例］　F=｛P［X，f（y），y］，P［X，f（B），B］｝，可使Q=｛A／X，B／Y｝

有：P［X，f（y），y］Q=P［A，f（B），B］　P［X，f（B），B］Q=P［A，f（B），B］

注：置换和合一是不唯一的。

定义2：设g是公式集F的一个合一，如果对F的任意一个合一S都存在一个置换λ，使得S=g·λ，则称g是一个最一般合一（Most General Unifier，简记为mgu）。

对一组表达式来说，最一般合一式是唯一的，除了字母的不同，即一个变元名到底是X还是Y，这对于合一的一般性是无所谓的。

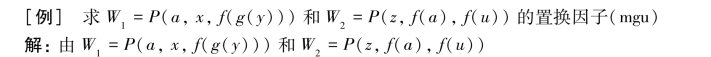
知：E=｛a／z，x／f（a），g（y）／u｝

定义3：设有一非空有限公式集F=｛F1，F2，…，Fn｝，从F中各公式的第一个符号同时向右比较，直到发现第一个彼此不尽相同的符号止，从F的各个公式中取出那些以第一个不一致符号开始的最大的子表达式为元素，组成一个集合D，称为F的分歧集（Disagreement set）。

2）合一算法

设F为非空有限表达式集合，则可按下列步骤求其mgu：

（1）置k=0，Fk=F，σk=ε（空置换，即不含元素的置换）。

（2）若Fk只含有一个表达式，则算法停止，σk就是所要求的mgu。

（3）找出Fk的分歧集Dk。

（4）若Dk中存在元素ak和tk，其中ak是变元，tk是项，且ak不在tk中出现，则置：，然后转向（2）。

（5）算法停止，F的mgu不存在。