命题是反映判断的句子，不反映判断的句子不是命题，而且命题具有很大的局限性。

例如：张三星期一至星期五都在教室上自习。

如果用P表示张三上自习，用P1表示张三星期一上自习，用P2表示张三星期二上自习，…用P5表示张三星期五上自习，该问题用命题公式表示，则可表示为：P∧P1∧P2∧

P3∧P4∧P5。

可以看出，命题逻辑能够表示客观世界的各种事实，但是不适合表达比较复杂的问题。

1.谓词的概念与表示

谓词用于刻画客体的性质或关系，可以简洁地表示用命题表示起来较复杂的事件，甚至能表达无法用命题逻辑表达的事情。

上述问题，如果用P表示张三上自习，用1，…，5表示星期一至星期五，则用谓词表示如图2-35所示。

图2-35　谓词表示事件

注意：用谓词表达命题，必须包括客体和谓词字母两个部分。

例如：

（1）他是三好学生。

（2）7是质数。

（3）每天锻炼身体是好习惯。

（4）5大于3。

（5）哥白尼指出地球绕着太阳转。

在上述语句中，前三个是指明客体性质的谓词，后两个是指明两个客体之间关系的谓词。

“b是A”类型的命题可用谓词A（b）表达。

“a小于b”这种两个客体之间关系的命题，可用谓词表达为B（a，b），这里B表示“小于”。

通常把A（b）称作一元谓词，B（a，b）称作二元谓词，L（a，b，c）称作三元谓词，依次类推。一元谓词表达了客体的“性质”，多元谓词表达了客体之间的关系。

2.谓词演算的语法和语义

谓词演算是一种形式语言，能用数学演绎的方式导出一个新的语句，并且能够判断这个语句的正确性。

谓词演算是人工智能中一种常用的知识表示方法，可表示各种描述语句，例如在产生式系统中，用来表达综合数据库、规则集的描述等。谓词演算体系中的一些演绎推理方法，还可用来建立自动定理证明系统、问答系统、基于规则的演绎系统等。

谓词演算联结词¬、∧、∨、→、↔的意义与命题演算中的解释完全相同。

例如：设S（x）表示“x学习很好”，用W（x）表示“x工作很好”。则¬S（x）表示“x学习不是很好”。S（x）∧W（x）表示“x的工作、学习都很好”。S（x）→W（x）表示“x的学习很好，则x的工作得很好”。

定义1　谓词演算符号的字母表

谓词演算符号的字母表组成如下：

（1）英语字母集合，包括大写与小写，如A，a，B，b，…

（2）数字集合，如0，1，…，9

（3）下划线

注意：该字母表中不包括#，%，@，1，&，“，”等字符。

定义2　谓词演算的符号集和项的概念

（1）谓词演算的符号集包括如下元素：

①真值符号：true，false。

②常元符号：第一个字符为小写字母的符号表达式。常元指世界中特定事物或特性命名，如tree，blue等。

③变元符号：第一个字符为大写字母的符号表达式。变元符号用于命名世界的一般类型的对象或特性，如George，Bill，Kate等。

④函词符号：第一个字符为小写字母的符号表达式，函词有一个元数，指出从定义域中映射到值域中的每个元素。函词代表从一个集合（称为函词的定义域）的一个元素或多个元素，到另一个集（值域）的唯一元素的映射。

⑤连接词：∨、∧、¬、→，↔。

⑥谓词演算中的量词：

“∀”全称量词，表示“任一”的意义。

“∃”存在量词，表示存在“某一”的意义。

（2）项的概念。一个项是一个常元或变元或函词表达式。函词表达式是函词符号后面加上它的参数，参数是函词定义域中的元素，参数的个数等于函词的元数，参数用括号括起来，并用逗号隔开，如f（X，Y，Z）。

一个n元函词表达式项以n元函词表达式开头，后跟用括号括起来的n个项——t1，t2，…，tn，项间用逗号分开，如f（t1，t2，…，tn）

注意：函词和函数有同等意义，只是这里的函词对应为离散概念。函数和函词的比较如图2-36所示。

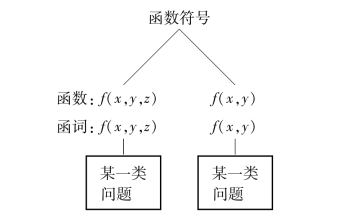
图2-36　函数和函词比较

定义3　谓词演算的命题

每个原子命题是命题。

如果S是命题，那么¬S也是命题。

如果S1，S2是命题，那么S1∧S2，S1∨S2，S1→S2，S1↔S2也都是命题。如果x是一个变元，S是一个命题，那么（∀x）S，（∃x）S也是命题。

定义4　一阶谓词演算

一阶谓词之间的运算称其为一阶谓词演算。

注意：一阶谓词演算只允许约束变元代表论域中的对象，而不能代表谓词或函词，如图2-37所示。

∀（likes）likes（george，kate）不是一阶谓词的合式表达式，但在高阶谓词演算中是有意义的。

图2-37　谓词演算

［例1］　“George和Kate、Susie是朋友”可表示为friends（george，susie）∧friends（george，kate），此时的真值指派为T。若George和Kate不是朋友，则第一式指派为T，第二式指派为F。

［例2］　把下列英文句子翻译成谓词表达式。

（1）All basketball players are tall：∀X（basketball-player（X）⇒tall（X））

（2）Some people like anchovies：∃X（person（X）∧likes（X，anchovies））

（3）Nobody likes taxes：¬∃X likes（X，taxes）

［例3］　用谓词表示圣经家谱中的家庭成员的关系。

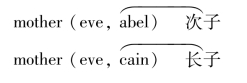
father（adam，abel）

father（adam，cain）

（∀X）（∀Y）（（father（X，Y）∨mother（X，Y））→parent（X，Y））

（∀X）（∀Y）（∀Z）（（parent（X，Y）∧parent（X，Z））→sibling（Y，Z）

3.谓词演算的基本关系式

（1）蕴涵等价式：

P（X）→Q（X）≡¬P（X）∨Q（X）

（2）德·摩根律：

¬（P（X）∨Q（X））≡¬P（X）∧¬Q（X）

¬（P（X）∧Q（X））≡¬P（X）∨¬Q（X）

（3）分配律：

P（X）∧（Q（X）∨R（X））≡（P（X）∧Q（X））∨（P（X）∧R（X））

P（X）∨（Q（X）∧R（X））≡（P（X）∨Q（X））∧（P（X）∨R（X））

（4）交换律：

P（X）∧Q（X）≡Q（X）∧P（X）

P（X）∨Q（X）≡Q（X）∨P（X）

（5）结合律：

（P（X）∧Q（X））∧R（X）≡P（X）∧（Q（X）∧R（X））

（P（X）∨Q（X））∨R（X）≡P（X）∨（Q（X）∨R（X））

（3）全称量词与存在量词的否定：

¬（∃X）P（X）≡（∀X）¬P（X）

¬（∀X）P（X）≡（∃X）¬P（X）

（4）变元代换：

（∃X）P（X）≡（∃Y）P（Y）

（∀X）Q（X）≡（∀Y）Q（Y）

（5）作用域分解：

（∀X）（P（X）∧Q（X））≡（∀X）（P（X））∧（（∀Y）（Q（Y））

（∃X）（P（X）∨Q（X））≡（∃X）P（X）∨（∃Y）Q（Y）

4.逻辑表示应用举例

［例1］　积木世界（见图2-38）。

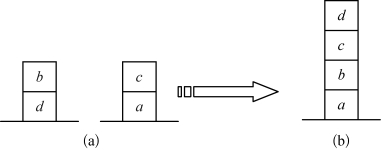
图2-38　积木世界

（a）初始状态　（b）目标状态

初始状态可描述为：on（c，a），on（b，d），ontable（a），ontable（d），clear（c），clear（b），hand_empty

目标状态描述为：on（b，a）∧on（c，b）∧on（d，c）∧ontable（a）∧hand_empty下述的规则描述了何时积木顶上为空：

∀X（¬∃Y on（Y，X）→clear（X））

描述将一个积木堆放在另一个积木顶上的规则：

∀X∀Y（hand_empty∧clear（X）∧clear（Y）∧pick_up（X）∧put_down（X，Y）→stack（X，Y））

［例2］　梵塔难题。

有3个柱子（1、2和3）和3个不同尺寸的圆盘（A、B和C）。在每个圆盘的中心有个孔，所以圆盘可以堆叠在柱子上。最初，全部3个圆盘都堆在柱子1上，最大的圆盘C在底部，最小的圆盘A在顶部。要求把所有圆盘都移到柱子3上，每次只许移动一个，而且只能搬动柱子顶部圆盘，还不许把尺寸大的圆盘堆在尺寸小的圆盘上。(www.daowen.com)

这个问题的初始状态和目标状态如图2-4所示。

解：先将问题化成谓词公式。

（1）盘：disk（X）　X∈｛A，B，C｝。

（2）针：pee（X）　X∈｛1，2，3｝。

（3）盘的大小：

∀X∀Y∀Z（smaller（X，Y）∧smaller（Y，Z）→smaller（X，Z））

表示：X＜Y　且　Y＜Z→X＜Z，　X，Y，Z∈｛A，B，C｝

题中的常量：smaller（A，B）∧smaller（B，C）

表示：A＜B　且　B＜C

由此显然有：smaller（A，B）∧smaller（B，C）→Smaller（A，C）

（4）状态sit。

on（X，Y，S）表示在状态S中，X盘位于Y之上。

（5）X上没有盘。

∀X∀S（free（X，S）≡¬∃Y（on（Y，X，S））

表示在S状态下，X上是空的或不存在Y在X上。

legal的定义：

∀X∀Y∀Slegal（X，Y，S）≡（free，（X，S）∧free（Y，S）∧disk（X）∧smaller（X，Y）

表示：在状态S下，X到Y的移动是合理的，当且仅当X，Y是自由的，且Y较大。

（6）∀S∀S′∀X∀Y·S′=move（X，Y，S）→（on（X，Y，S′）∧∀ZZ1·（（¬（Z=X）∧¬（Z1=Y）→（on（Z，Z1，S）≡on（Z，Z1，S′））∧∀Z（on（X，Z，S）→free（Z，S′）））

表示：在两个对象和状态上，产生一个新状态，其中第一个对象在第二个对象之上，将这种新状态记为S′，S′表示移动后X在Y之上，若X原来在另一个对象Z上，则Z为自由，其他对象状态不变。

S′的定义：

当move合法时，S′将变成一个新的状态：

∀XYS，Legal（X，Y，S）≡situation（move（X，Y，S））

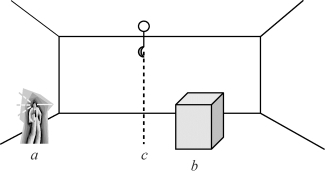
图2-39　猴子和香蕉问题

［例3］　猴子和香蕉问题（见图2-39）。

假设房间里有一个机器人“猴子”，位于a点。c点上方的天花板上有一串香蕉，“猴子”想得到它，但是够不着。房间内的b点还有一只箱子。如果“猴子”站到箱子上，就可以够着天花板。试为“猴子”制定一个得到香蕉的行动计划。

首先，用一阶谓词对问题进行形式化的描述。假定谓词locat（X，Y，S）表示在S状态下X位于Y处，S0为初始状态，则：

猴子为了得到香蕉，首先得走近箱子。

谓词go（X，Y，S）表示在S状态，猴子由X走到Y处：

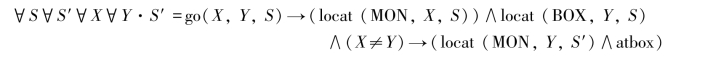
其中S′表示经go谓词后，出现的新状态，谓词atbox没有自变量，它表示猴子已经位于箱子处，即locat（MON，Y，S′）∧locat（BOX，Y，S′）。

谓词push（X，Y，S）的作用是在状态S中，猴子推着箱子从X处移动到Y处，该谓词的定义如下：

其中underbanana（S′）表示在状态S′时，猴子和箱子都在香蕉的正下方。

分别定义谓词standon（S），getbanana（S）分别表示登上箱和获取香蕉的操作。

有以下等式：

当猴子和箱子都在香蕉的正下方时，猴子就可以登上箱子，获取香蕉，从而求解了该问题，其中S，S，S″分别表示猴子所处的三个状态。

［例4］　史密斯家族聚会问题。

史密斯家族几十年来第一次聚到一起。四个姐妹已结婚，通过随意的交谈，他们发现了某些共同的习惯和兴趣，能使两对或更多的夫妇一起度过一个令人愉快的假期。

夫妇们的兴趣和习惯种类是：

（1）饮食爱好和习惯

（2）娱乐偏爱

（3）度假偏爱

（4）早上起床时间

夫妇们的兴趣和习惯以及名字已被存入数据库中，要求用户根据所给的信息，找出两对有类似兴趣的夫妇。

创建一个数据库和一组规则，数据库谓词married（X，Y）表示X与Y结婚，Y的个体域是四个姐妹，X的个体域是她们的丈夫。

与夫妇们的习惯和兴趣有关的谓词有：

diet（X，Y1）：X喜欢食物Y1。

entertainment（X，Y2）：X娱乐偏爱是玩Y2。

location（X，Y3）：X喜欢度假日去Y3旅游。

rise_time（X，Y4）：X喜欢早上起床时间是Y4。

X的个体域是夫妇中丈夫的名字，Yi是对话中所表达的数据。夫妇中如果对某种兴趣或习惯无所谓，将导致生成两个谓词。

例如，“约翰喜欢到任何地方旅游”可表示成：

location（John，city）

location（John，country）

这两个谓词都可以用在匹配处理中。

假定数据库中给出了该问题的初始状态，共有五类谓词：

（1）描述已婚夫妇对的谓词：

married（“John”，“Mary”）

married（“Sam”，“Jand”）

married（“Ron”，“Amy”）

married（“Bill”，“Alice”）

（2）描述夫妇对饮食爱好和习惯的谓词（第一个体为夫妇对中丈夫的名字，以下同）：

diet（“John”，“vegetarian”）

diet（“Sam”，“non-vegetarian”）

diet（“Ron”，“vegetarian”）

diet（“Ron”，“non-vegetarian”）

diet（“Bill”，“vegetarian”）

diet（“Bill”，“non-vegetarian”）

（3）描述夫妇对兴趣爱好的谓词：

entertainment（“John”，“movies”）

entertainment（“Sam”，“movies”）

entertainment（“Ron”，“movies”）

entertainment（“Ron”，“dancing”）

entertainment（“Bill”，“dancing”）

（4）描述夫妇对度假偏爱的谓词：

location（“John”，“city”）

location（“John”，“country”）

location（“Sam”，“country”）

location（“Ron”，“country”）

location（“Bill”，“city”）

（5）描述夫妇对早起习惯的谓词：

rise_time（“John”，“early”）

rise_time（“Sam”，“late”）

rise_time（“Ron”，“early”）

rise_time（“Bill”，“late”）

现在定义谓词sameinterest（X，Y）表示两对夫妇对以上四类均有共同兴趣，其中X，Y分别表示两对不同夫妇对中丈夫的名字。

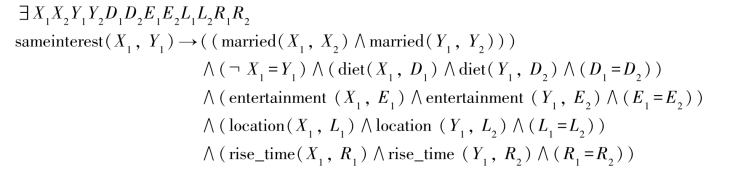
然后，根据以上规则逐条匹配数据库中的事实，直到找到两对兴趣完全相同的夫妇，或者干脆找不到。

结论：

一阶谓词逻辑要求一个确切的句法、语义以及真值和推理符号。弄清想要表达的是什么以及如何根据一事实集合推导出可能的结果，是逻辑形式化最为鲜明的特色。

逻辑表示的主要优点有：

（1）逻辑表示是表达各种符号的极其自然的方法。

（2）逻辑表示非常精确，确定一个目标表达式的真假，或找出达到目标状态的操作过程是按照严格的演绎结构实现的。这种演绎结构可以保证其求解过程是正确的，而且演绎过程可以完全形式化以便在计算机中实现，其他几种知识表示模式则很难做到。

（3）逻辑表示极其灵活。因为逻辑知识表示对实际做出的推论的处理种类没有限制，对特殊事实可按任一种方法表达而不必考虑可能性。

（4）逻辑表示很标准，且模块性好。逻辑推理是公理集合中演绎而得出结论的过程。逻辑及形式系统所具有的重要性质，可以保证知识库中新旧知识在逻辑上的一致性（或通过一套相应的处理过程检验）和所演绎出来的结论的正确性。而其他的表示方法在这点上还不能与其相比。

尽管逻辑表示法在实际人工智能系统上得到应用，但此方法仍然有一定的缺点：

（1）逻辑表示模式表达和处理分离。

（2）谓词表示越细、表示越清楚，推理越慢、效率越低。

（3）具有归纳结构的知识、多层次的知识类型都难以用一阶谓词来描述。