当把一个复杂问题归约为一组本原问题时，其归约过程可以用一个与/或图来表示，其中起始节点对应于原始问题描述，终叶节点对应于本原问题。

1.与图

当把一个复杂问题P分解为若干个子问题P1、P2、…、Pn时，可用一个“与图”来表示这种分解，P称为“与”节点。

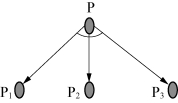
图2-30　与图　

例如，设问题P可以分解为P1、P2、P3这3个子问题，即对问题P的求解相当于同时求解问题P1、P2、P3，则P与P1、P2、P3之间的关系可用如图2-30所示的“与图”表示。

2.或图

当把一个复杂问题P变换为若干个与之等价的新问题P1、P2、…、Pn时，可用一个“或图”来表示这种变换，P称为“或”节点。例如，设问题P可以变换为P1、P2、P3这3个新问题中的任何一个，即P与这3个新问题中的任何一个都是等价的，于是问题P1、P2、P3中的任何一个被求解，即问题P得到求解则P与P1、P2、P3之间的关系可用如图231所示的“或图”表示。

3.与/或图

如果一个问题既需要通过分解，又需要通过变换才能得到其本原问题，则其求解过程可用“与/或图”来表示，如图2-32所示。

图2-31　或图

4.可解节点

与/或图中一个可解节点的一般定义如下：

（1）终叶节点是可解节点。

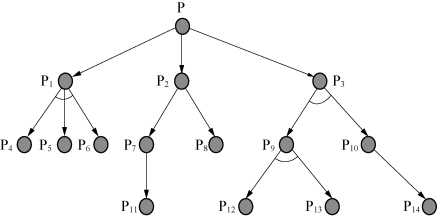
图2-32　与/或图

（2）若某个非叶节点含有或后继节点，则只有当其后继节点至少有一个是可解的，此非终叶节点才是可解的。(www.daowen.com)

（3）若某个非终叶节点含有与后继节点，则只要当其后继节点全部为可解的，此非终叶节点才是可解的。

5.不可解节点

当与/或图中某些非终叶节点没有后继节点时，就认为它是不可解的。不可解节点的出现，可能意味着图中包括起始节点在内的另外一些节点，也是不可解的。

不可解节点一般定义如下：

（1）没有后裔的非终叶节点为不可解节点。

（2）若某个非终叶节点含有或后继节点，则只有当其全部后裔为不可解时，此非终叶节点才是不可解的。

（3）若某个非终叶节点含有与后继节点，则只要其后裔至少有一个为不可解时，此非终叶节点就是不可解的。

6.用与/或图表示问题的步骤

（1）对所要求的问题进行分解或等价变换。

（2）若所得的子问题不是本原问题，则继续分解或变换，直到分解或变换为本原问题。

（3）在分解或变换中，若是不等价的分解，则用“与图”表示；若是等价变换，则用“或图”表示。

7.与/或图的构成规则

（1）与/或图中的每个节点代表一个要解决的单一问题或问题集合，起始节点对应于原始问题。

（2）对应于本原问题的节点，称作终叶节点，它没有后裔。

（3）对于把算符应用于问题P的每种可能情况，都把问题变换为一个子问题集合；有向弧线自P指向后继节点，表示所求得的子问题集合。

（4）对于代表两个或者两个以上子问题集合的每个节点，有向弧线从此节点指向此子节点问题集合的各个节点。由于只有当集合中所有项都有解时，这个子问题的集合才能获得解答，所以这些子问题节点称作与节点。为了区别于或节点，把具有共同父辈的与节点后裔的所有弧线用另外一小弧线连接起来。

（5）特殊情况下，当只有一个算符可应用于问题，而且这个算符产生具有一个以上子问题的某个集合时，代表子问题集合的中间或节点可以省略。

用与/或图法求解问题的解图是由可解节点构成，并且可由这些可解节点推出包含对应着原始问题的初始节点，解图是可解节点的子图。