1.正向推理

正向推理是指从初始状态开始，在规则的控制下向目标状态一步步移动，直至到达目标状态。正向推理也称数据驱动方式或自底向上的方式。推理过程是：

（1）规则库中的规则与数据库中的事实进行匹配，得到触发规则集合。（2）从触发规则集合中选择一条规则作为启用规则（冲突解决）。

（3）执行启用规则，将该使用规则的后件送入数据库。

重复这个过程直至达到目标。

具体说如数据库中含有事实A，而规则库中有规则A→B，那么这条规则便是触发规则，进而将后件B送入数据库。这样可不断扩大数据库直至包含目标。若有多条触发规则，需从中选一条作为启用规则。不同的选择方法直接影响求解效率，选规则的问题就是控制策略。正向推理会得出一些与目标无直接关系的事实，是有浪费的。

正向推理的基本过程如图2-25所示。

图2-25　正向推理

正向推理算法：

（1）将初始事实、数据置入动态数据库。

（2）用动态数据库中的事实/数据，匹配/测试目标条件，若目标条件满足，则推理成功，结束。

（3）用规则库中各规则的前件匹配动态数据库中的事实/数据，将匹配成功的规则组成触发规则集。

（4）若触发规则集为空，则运行失败，退出。

（5）将触发规则集中的规则放入冲突集中。根据冲突解决策略决定启用规则并执行之，将该规则的结论加入动态数据库，转步骤（2）；

［例1］　某树类型辨识产生式系统，可模拟植物学家的思维过程，在一系列产生式规则的指导下，通过某些线索（如叶子的形状等）来推断树的类型。该系统由规则库、数据库、控制器三部分组成。控制器仅提供了两个函数：on_vm（x），用来测试树的识别特征x是否存在于数据库VM中；put_on_vm（x），在一条规则被启用后，把树的识别特征x添加到VM中。

规则库包含的基本规则如下：

R1：if on_vm（叶子脱落）then put_on_vm（落叶树）

R2：if on_vm（叶子保持）then put_on_vm（常青树）

R3：if on_vm（阔叶and非银杏）then put_on_vm（被子植物）

R4：if on_vm（针叶）then put_on_vm（裸子植物）

R5：if on_vm（一子叶）then put_on_vm（单子叶植物）

R6：if on_vm（二子叶）then put_on_vm（双子叶植物）

R7：if on_vm（单子叶植物）or on_vm（双子叶植物）then put_on_vm（被子植物）

R8：if on_vm（松树球果）then put_on_vm（裸子植物）

R9：if on_vm（二针叶）or on_vm（三针叶）or on_vm（五针叶）or on_vm（簇针叶）then put_on_vm（针叶）

R10：if on_vm（被子植物）and on_vm（落叶树）and on_vm（叶子密集）then put_on_vm（糖槭）

Rll：if on_vm（被子植物）and on_vm（常青树）and on_vm（叶子密集）then put_on_vm（冬青树）

R12：if on_vm（被子植物）and on_vm（落叶树）and on_vm（复合叶子）then put_on_vm（核桃树）

R13：if on_vm（裸子植物）and on_vm（常青树）and on_vm（三针叶）then put_on_vm（Ponderosa松树）

R14：if on_vm（裸子植物）and on_vm（落叶树）and on_vm（簇针叶）then put_on_vm（落叶松树）

R15：if on_vm（裸子植物）and on_vm（常青树）and on_vm（五针叶）then put_on_vm（白松树）

控制器以适当的顺序应用以上规则，模拟植物学家的思维过程，按照产生式系统的工作周期运行，进行树类型的辨识工作。假设系统启动后，通过观察已经获得了三个事实——松树球果、簇针叶、叶子脱落，并把它们添加到了VM中，使VM包含三个元素，即

在产生式系统工作的第一周期中，模式匹配阶段把所有规则的前件与VM中的三个元素进行比较测试，发现规则R1、R8、R9匹配成功，把这三条规则放入冲突集中。在冲突消解阶段，根据本系统的冲突消解策略——优先启用编号最小，且其后件部分不在VM中的规则，启用了规则R1。在执行阶段执行R1后件定义的动作，其结论“落叶树”被添加到VM中。于是，在第一周期结束时VM中包含四个元素，即

在第二周期中，重新检查所有规则，进行模式匹配，仍然是规则R1、R8、R9匹配成功。根据冲突消解策略，虽然R1编号最小，但因其结论“落叶树”已存在于VM中，不能被启用，于是，编号次小的规则R8被启用，其结论“裸子植物”添加到了VM中。这样，第二周期结束时，VM中包含五个元素，即

在第三周期中，规则R1、R8、R9、R14匹配成功，根据冲突消解策略，规则R9被启用，VM中添加了其结论“针叶”。于是，在第三周期结束时VM中包含了六个元素，即

在第四周期中，规则R1、R4、R8、R9、R14匹配成功，规则R14被启用，VM中添加了其结论“落叶松树”。于是，第四周期结束时VM中包含七个元素，即

在第五周期中，仍是规则R1、R4、R8、R9、R14匹配成功，但这些规则的结论均已包含在VM中，在冲突集中找不到可以应用的规则，于是产生式系统的推理过程结束，获得了系统的最终结论：由初始事实所推断出的树是“落叶松树”。

［例2］　动物分类问题的产生式系统描述及其求解。

设由下列动物识别规则组成一个规则库，推理机采用上述正向推理算法，建立一个产生式系统。该产生式系统就是一个小型动物分类知识库系统。规则：

R1：若某动物有奶，则它是哺乳动物。

R2：若某动物有毛发，则它是哺乳动物。

R3：若某动物有羽毛，则它是鸟。

R4：若某动物会飞且生蛋，则它是鸟。

R5：若某动物是哺乳动物且有爪且有犬齿且目盯前方，则它是肉食动物。

R6：若某动物是哺乳动物且吃肉，则它是肉食动物。

R7：若某动物是哺乳动物且有蹄，则它是有蹄动物。

R8：若某动物是有蹄动物且反刍食物，则它是偶蹄动物。

R9：若某动物是肉食动物毛发黄褐色且有黑色条纹，则它是老虎。

R10：若某动物是肉食动物毛发黄褐色且有黑色斑点，则它是金钱豹。

R11：若某动物是有蹄动物长腿、长脖子且毛发黄褐色有暗斑点，则它是长颈鹿。

R12：若某动物是有蹄动物毛发白色且有黑色条纹，则它是斑马。

R13：若某动物是鸟不会飞、长腿、长脖子且毛发黑白色，则它是鸵鸟。

R14：若某动物是鸟不会飞、会游泳且毛发黑白色，则它是企鹅。

R15：若某动物是鸟善飞且不怕风浪，则它是海燕。

再给出初始事实：

f1：某动物有毛发。

f2：吃肉。

f3：黄褐色。

f4：有黑色条纹。

目标为：该动物是什么？

推理过程：

初始状态　VM=（某动物有毛发，吃肉，黄褐色，有黑色条纹）

产生式系统工作的第一周期，R2匹配成功，执行之，此时

VM=（哺乳动物，某动物有毛发，吃肉，黄褐色，有黑色条纹）

产生式系统工作的第二周期，R6匹配成功，执行之，此时

VM=（肉食动物，哺乳动物，某动物有毛发，吃肉，黄褐色，有黑色条纹）

产生式系统工作的第三周期，R9匹配成功，执行之，此时

VM=（老虎，肉食动物，哺乳动物，某动物有毛发，吃肉，黄褐色，有黑色条纹）

在第四周期中，仍是规则R2、R6、R9匹配成功，但这些规则的结论均已包含在VM中，在冲突集中找不到可以应用的规则，于是产生式系统的推理过程结束，获得了系统的最终结论：由初始事实所推断出的动物是“老虎”。

2.反向推理

反向推理是从目标（作为假设）出发，反向使用规则，求得已知事实（初始状态）。反向推理也称目标驱动方式或自顶向下的方式，推理过程是：

（1）规则集中的规则后件与目标事实进行匹配，取得匹配的规则集合。

（2）从匹配规则集中选择一条规则作为使用规则。

（3）将使用规则的前件作为子目标。

重复这个过程直至各子目标均为已知事实成功结束。

如果目标明确，则使用反向推理方式效率较高，所以反向推理常为人们所使用。

反向推理的基本过程如图226所示。

图2-26　反向推理

反向推理算法：

（1）将初始事实/数据置入动态数据库，将目标条件置入目标链。

（2）若目标链为空，则推理成功，结束。

（3）取出目标链中第一个目标，用动态数据库中的事实/数据同其匹配，若匹配成功，转步骤（2）。(www.daowen.com)

（4）用规则集中的各规则的结论同该目标匹配，若匹配成功，则将第一个匹配成功且未用过的规则的前提作为新的目标，并取代原来的父目标而加入目标链，转步骤（3）。

（5）若该目标是初始目标，则推理失败，退出。

（6）将该目标的父目标移回目标链，取代该目标及其兄弟目标，转步骤（3）。

［例］　某产生式系统用于桌面出版系统配置咨询，其规则库内容如下：

R1：　if　budget_considerations=ok　and　hardware=found then　find_rec=ok

R2：　if　budget_ceiling=high　or　budget＞1000 then　budget_considerations=ok

R3：　if　hardware≠found　then　find_rec≠ok

R4：　if　find_rec≠ok then　advice=“There's a problem with your configuration”

R5：　if　budget_considerations≠ok then　advice=“Can't afford desktop publishing”

R6：　if　printer=known　and　monitor=known　and　computer=known then　hardware=found

假定系统给定的初始目标是find_rec，工作存储器VM的初始内容为VM=（printer=known，monitor=known，computer=known），则系统进行反向推理的过程如下：

（1）由于反向推理由目标驱动，仅考虑直接与目标有关的规则和事实，因此推理机首先搜索规则库，寻找包含初始目标“find-rec”的规则。R1符合条件，被选中。

（2）因为R1包含两个条件，推理机先检查其第一个条件。在VM中搜索属性budget_considerations的值，但VM中没有关于budget_considerations的事实。由于此条件不是叶子节点，于是把budget_considerations作为当前目标，以便搜索可能包含budget_considerations值的其他资源，而初始目标find-rec被压入暂存目标堆栈中（当对budget_considerations的搜索终止时，可将初始目标find-rec从暂存目标堆栈中弹出，恢复为当前目标）。

（3）搜索规则库。寻找包含目标“budget_considerations”的规则，R2被选中。

（4）检查R2的第一个条件，测试其属性budget_ceiling的值是否为“high”。推理机搜索VM，试图确定budget_ceiling的值，但VM中没有关于budget_ceiling的信息，于是把budget_ceiling作为当前目标，而把budget_considerations压入暂存目标堆栈中。

（5）搜索规则库，寻找包含目标“budget_ceiling”的规则，没有找到。

（6）向用户询问“budget_ceiling”的值，用户回答“unknown”，R2的第一个条件子句匹配失败。于是budget_ceiling不再作为当前目标，被从当前目标存储器中移去，而budget_considerations被从暂存目标堆栈中弹出，恢复为当前目标。

（7）由于R2的两个条件是“或”关系，只要其中之一为真，R2即可为真，所以推理机开始考虑R2的第二个条件，测试其属性budget的值，把budget作为当前目标，budget_considerations再次被压入暂存目标堆栈中。但在VM中找不到关于“budget”的事实，于是询问用户。

（8）用户回答“2000”，此值被赋予属性budget，并把“budget=2000”作为新事实添加到VM。由于budget已有值约束，不再作为当前目标，budget_considel再次从暂存目标堆栈中弹出，恢复为当前目标。此时：

VM=（budget=2000，printer=known，monitor=known，computer=known）

因为VM发生了变化，推理机重新测试R2的第二个条件。现在“budget＞1000”的条件成立，R2为真，被启用，其后件属性“budget_considerations”被赋值为“OK”，并添加到VM中。这时：

VM=（budget_considerations=ok，budget=2000，printer=known，monitor=known，computer=known）

（9）由于budget_considerations已获解，不再作为当前目标。初始目标find_rec从暂存目标堆栈中弹出，恢复为当前目标，推理机返回到R1，测试R1第一个条件的值，测试结果为真。

（10）考虑R1的第二个条件，测试属性hardware的值，在VM中没有发现关于“hardware”的事实，于是取hardware为当前目标，初始目标find-rec再次被压入暂存目标堆栈。

（11）搜索规则库，寻找包含目标“hardware”的规则，R6被选中。

（12）测试R6的三个条件。

（13）R6的三个条件与VM中的三个事实匹配成功，R6为真，被启用，其结论“hardware=found”被添加到VM中。此时：

VM=（hardware=found，budget_considerations=ok，budget=2000，printer=known，monitor=known，computer=known）

（14）从暂存目标堆栈中弹出初始目标find-rec，恢复其为当前目标，测试R1第二个条件的值，因为VM中已有了“hardware=found”的事实，此条件为真。

（15）R1的两个条件均为真，R1为真，find_rec被赋值“OK”。

由于系统初始目标find_rec已经确定，所有当前目标已被释放，暂存目标堆栈中已没有其他目标，于是推理机停止运行，系统给出推理结论“find_rec=ok”，即桌面出版系统配置已经成功。

3.双向推理

双向推理也称混合推理。双向推理既自顶向下，又自底向上作推理，直至某个中间界面上两方向结果相符便成功结束。不难想象，这种双向推理较正向或反向推理所形成的推理网络来得小，从而推理效率更高。

双向推理的基本过程如图2-27所示。

图2-27　双向推理

双向推理算法描述：

函数select_hapothesis使用前一步产生的事实，以选择系统下一步试图满足的目标。

4.产生式系统的应用实例

［例］　传教士和野人问题（Missionaries and cannibals）：

有N个传教士和N个野人来到河边准备渡河，河岸有一条船，每次至多可供K个人乘渡。问传教士为了安全起见，应如何规划摆渡方案，使得任何时刻河岸两边以及船上的野人数目总是不超过传教士的数目。即求解传教士和野人从左岸全部摆渡到右岸的过程中，任何时刻满足M（传教士数）≥C（野人数）和M+C≤K的摆渡方案。

该问题使用状态空间图和产生式系统相结合的方法来解决。

设N=M=C=3，K=2，则给定问题的状态图如图2-28所示。

图中的L和R表示左岸和右岸，ML表示左岸传教士的人数，CL表示左岸野人的人数，BL表示左岸船只的状态，B=0或1分别表示无船和有船。约束条件是：两岸上M≥C，船上M+C≤2。

（1）综合数据库用三元组表示，即（ML，CL，BL），其中0≤ML≤3，0≤CL≤3，BL∈｛0，1｝，此时问题描述简化为

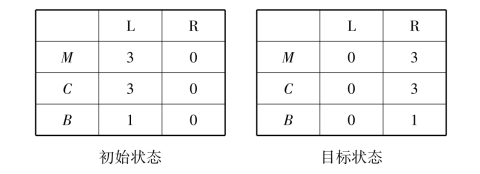
图2-28　传教士和野人问题状态

N=3的M—C问题，状态空间的总状态数为4×4×2=32。根据约束条件的要求，可以看出只有20个合法状态。进一步分析后，又发现有4个状态实际上是不可能达到的，因此实际问题空间仅由16个状态构成。下面列出分析结果。

（MLCLBL）

（0　0　1）达不到

（0　1　1）

（0　2　1）

（0　3　1）

（1　0　1）不合法

（1　1　1）

（1　2　1）不合法

（1　3　1）不合法

（2　0　1）不合法

（2　1　1）不合法

（2　2　1）

（2　3　1）不合法

（3　0　1）达不到

（3　1　1）

（3　2　1）

（3　3　1）

（0　0　0）

（0　1　0）

（0　2　0）

（0　3　0）达不到

（1　0　0）不合法

（1　1　0）

（1　2　0）不合法

（1　3　0）不合法

（2　0　0）不合法

（2　1　0）不合法

（2　3　0）不合法

（3　0　0）

（2　2　0）

（3　1　0）

（3　2　0）

（3　3　0）达不到

（2）规则集合：PMC操作规定M个传教士和C个野人从左岸向右岸；qMC操作规定M个传教士和C个野人从右岸向左岸。

船上人有5种组合，因而组成10条规则集合：

（3）摆渡方案的实现如图2-29所示。

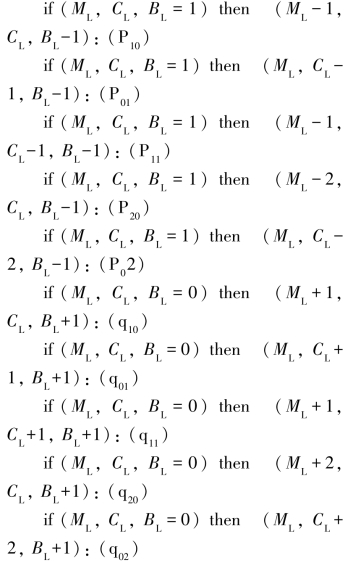
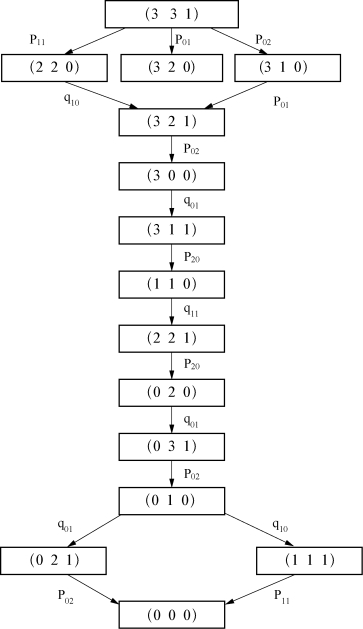
图2-29　传教士和野人过河方案