人工智能中的问题求解过程实际上是一个搜索过程。为了进行搜索，必须首先用某种形式把问题表示出来，其表示是否适当，将直接影响搜索效率。状态空间表示法就是用来表示问题及其搜索过程的一种方法。它是人工智能中最基本的形式化方法，也是讨论问题求解技术的基础。

1.问题状态描述

状态（State）是为描述某类不同事物间的差别而引入的一组最少变量q0，q1，…，qn的有序集合，其矢量形式为Q=［q0，q1，…，qn］T。式中每个元素qi（i=0，1，…，n）为集合的分量，称为状态变量。给定每个分量的一组值就得到一个具体的状态，如Qk=［q0k，q1k，…，qnk］T。

使问题从一个状态变化为另一个状态的手段称为操作符或算符。

操作符可分为走步、过程、规则、数学算子、运算符号或逻辑符号等。

2.状态空间描述

状态空间（State Space）是一个表示该问题全部可能状态及一切可用算符所构成的集合。它包括三种说明的集合，即所有可能的问题初始状态集合S，操作符集合F及目标状态集合G，因此可把状态空间表示为一个三元组：（S，F，G）。

状态空间的图示形式，即问题的全部状态及其关系的图称为状态空间图。其中节点表示状态，有向边表示关系。

［例1］　15数码问题（15 Puzzle problem）也称“十六宫”问题。指把用15个不同数字标注的牌放在有16个位置的网格上，空出一个位置，使将牌可以移动，形成不同的格局，如图2-2所示。

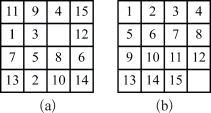
图2-2　15 Puzzle problem问题

（a）初始状态　（b）目标状态

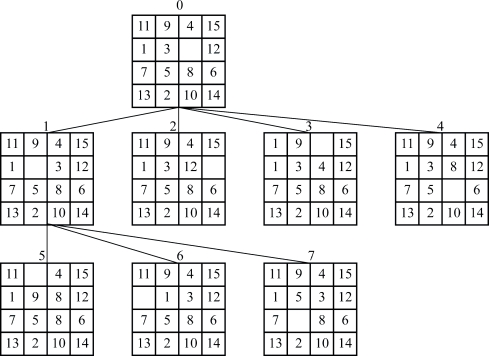
图2-3为该问题求解的部分状态空间。

(www.daowen.com)

图2-3　15 Puzzle problem问题的部分状态空间

［例2］　梵塔问题（Tower-of-Hanoi Puzzle）

传说在印度的贝那勒斯的圣庙中，主神梵天做了一个由64个大小不同的金盘组成的“梵塔”，并把它穿在一个宝石杆上。另外，旁边再插上两个宝石杆。然后，他要求僧侣们把穿在第一个宝石杆上的64个金盘全部搬到第三个宝石杆上。搬动金盘的规则是：一次只能搬一个，不允许将较大的盘子放在较小的盘子上。这就是梵塔问题。梵天预言：一旦64个盘子都搬到了3号杆上，世界将在一声霹雳中毁灭。

经计算，把64个盘子全部搬到3号杆上，需要穿插搬动盘子264－1=18 446 744 073 709 511 615次。所以直接考虑原问题将过于复杂。

现在考虑3盘片的梵塔问题：

用状态（i，j，k）表示最大盘片A在第i根针上，盘片B在第j根针上，最小盘片C在第k根针上。如果同一根针上有两片或两片以上的盘片，则假设较大的在下面，如图2-4所示。

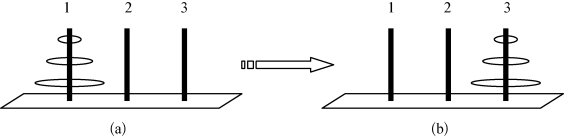
图2-4　3盘片的梵塔问题

（a）初始状态　（b）目标状态

其状态空间如图2-5所示。

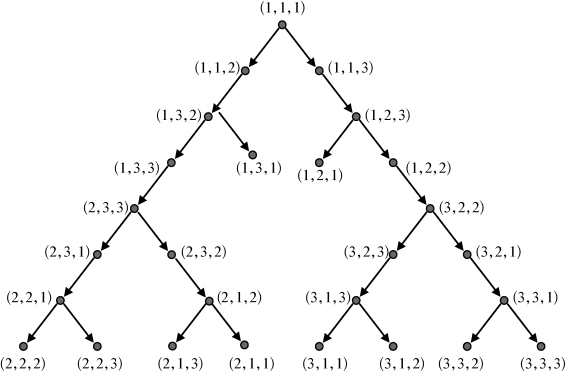
图2-5　3盘片的梵塔问题的状态空间

状态空间图实际上是一类问题的抽象表示。事实上，有许多智力问题（如梵塔问题、旅行商问题、八皇后问题、农夫过河问题等）和实际问题（如路径规划、定理证明、演绎推理、机器人行动规划等）都可以归结为在某一状态图中寻找目标或路径的问题。因此，研究状态空间图搜索具有普遍意义。