SAIL可能的聚束模式包括3种：①传统聚束模式，即SAIL做直线运动，在运动中光学足迹恒定地指准在被测目标平面内所关注的成像区域［见图12-9（a）］。②逆聚束模式，被测目标做直线运动而SAIL作跟踪使得光学足迹恒定地指准目标［图12-9（b）］。③层析聚束模式，SAIL与被测目标相对静止，被测目标在光学足趾中只做旋转运动。光学足趾是激光照明光斑和接收视场共同作用的目标面上的可成像面积。

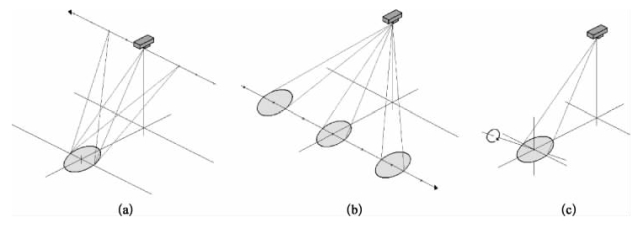
图12-9　合成孔径激光成像雷达聚束模式分类

（a）聚束模式；（b）逆聚束模式；（c）层析聚束模式

合成孔径激光成像雷达主要由3部分组成：①激光头，包括激光发射机、光电接收机和光学天线，其作用是进行目标的距离分辨测量或者目标的多普勒频移分辨测量，用于距离分辨时可以采用脉冲激光发射和强度直接探测，也可以采用脉冲激光发射和光学外差接收、脉冲啁啾激光发射和外差接收及解斜解调，用于多普勒频移分辨时可以采用连续单频激光发射和光学外差接收。②光学扫描器，用于目标的精密跟踪。③图像处理器。前两部分用于目标的数据收集而后一部分用于数据处理，进行图像重构。显然可见，本节的非相干处理聚束模式SAIL的硬件结构远比相干处理的SAIL［21～26］简单。

对于上述模式中的SAIL与目标的相对转动的描述可以用图12-10统一表示。基准参考面坐标系为（x，y），其垂直轴与雷达的交点为基准参考轴。中间参考面（x′，y′）相对于基准面转动θ角。目标物面（x″，y″），定义φ角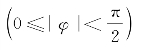为水平面倾角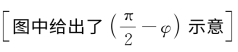。3个坐标系的重合原点与雷达的距离为Z。对于层析聚束模式θ角即为目标自旋角，对于传统聚束模式和逆聚束模式可以求得

式中，X为SAIL或者目标的移动距离。3个坐标系的重合原点与雷达的距离为Z（θ），即

垂直于基准参考面的入射点（x，y）对于其他两个面的坐标位置由图12-10可以求得

1）二维目标非相干处理距离分辨聚束模式

本小节讨论二维目标的距离分辨成像，SAIL进行侧视面激光测距的距离分辨投影，所得到的距离回波信号为光强或者振幅，因为非相干处理而不需要时间相位信息。应当注意，如前所述距离分辨测量可以采用相干探测，也可以采用直接探测，前者具有较高的探测灵敏度，但是接收视场受天线口径限制［27］，后者可以设计更大接收视场和更大天线口径。

SAIL对于目标的数据收集采用侧视面距离分辨投影积分，由图12-10的关系可以求得目标面上一点（x″，y″）所产生的相对于基准面的距离为

因此目标距离为Zk的等位线方程为

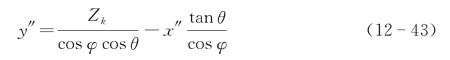
采用顺时针转动的坐标变换：

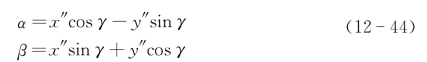
在转动角为如下时

事实上α轴平行于等位线，目标点（x″，y″）对于基准平面的距离在投影β轴上的位置为

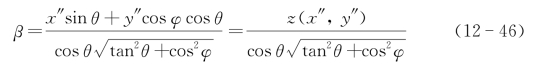
设目标函数为p（x″，y″），如前所述为光强或者场强振幅分布。则沿距离等位线α方向上的距离分辨的图像函数在β轴上投影的积分为一维函数：

采用计算机进行距离分辨CT层析解调来重构目标图像。反向投影算法、滤波反向投影算法和雷登-傅里叶变换是最基本的层析解调方法，其他方法还包括匹配滤波算法、Hough变换算法等［35～36］。从上述重构算法所得到的像可以进一步采用阈值处理等操作进行进一步的图像处理。

具体的CT解调原理和方法如下：

（1）反向投影算法。其目标像的层析计算公式为

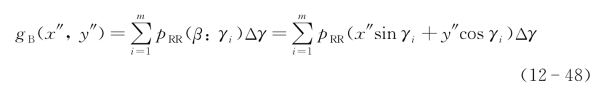
式中，γi为第i次投影的等效坐标系转角，Δγ是两次投影的角差，i是投影次数。

为了降低反向投影算法在重建中的条纹效应，提供较好的图像质量，可以使用滤波反向投影算法，即在反向投影之前先采用适当的修正。修正投影qR（β：γi）给定为

式中，F1和分别为相对于空间变量β的一维傅里叶变换和逆变换，f为傅里叶变换中的空间频率变量。采用滤波反向投影算法的重建图像为

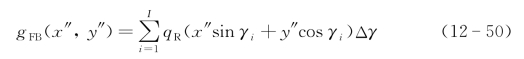
（2）雷登-傅里叶变换。基于投影-切片原理，即一个投影的傅里叶变换是该物体二维傅里叶变换的一个切片。因此对于物体作二维傅里叶变换为

对于投影作一维傅里叶变换：

则根据投影-切片理论，有

可见不同角度测量的投影所产生的傅里叶变换是通过坐标原点上不同直线上的数值分布。因此一系列的投影将产生图像的近似二维傅里叶变换，原则上重构像可以进一步采用逆傅里叶变换产生，其中有可能还需要采取插值或和极坐标-直角坐标变换处理［32］。

激光测距采用脉冲激光发射和强度直接探测方式时，激光脉冲宽度为Δτ，考虑到触发光脉冲误差则距离分辨全宽度为Δz=cΔτ。采用啁啾激光发射和外差解斜解调方式时，啁啾带宽为B，则距离分辨全宽度为。由此，测距误差产生的投影成像全宽度Δβ（θ）为

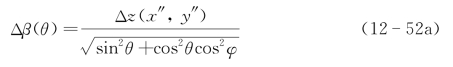
假定共有I个反投影成像，I个光强或振幅叠加的直径成为成像点最大值的直径，即取I阈值后的像点直径为

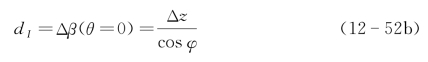
设γ=0和γ1的反投影交叉叠加光强或振幅为2的最大区域为成像点的可能最大边缘，代表成像点发散，即有

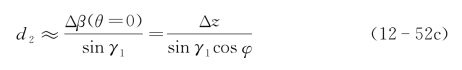
可见物面倾斜角φ越小则成像直径越小；转角间隔γ1越大则成像点发散越小。

根据距离分辨层析的成像分辨率，进一步研究非相干聚束SAIL的空间相位问题。目前可以认为接收处理电子学的带宽容易达到1.5 GHz，以此为据激光脉冲宽度为0.7 ns，则距离分辨率为10 cm。照明光斑和接收视场对于波前的平度在大约10 cm数量级上的要求远比相干处理SAIL的宽松得多，因为后者要求为十几到数百个波长的相位二次项［24～31］。

综上所述，非相干聚束SAIL可以达到的成像分辨率在原理上低于相干处理SAIL大约一个数量级，但是相对于光频的空间相位分布和频率时间相位同步而言无严格要求。

为了充分理解非相干聚束SAIL的侧面CT层析投影和重构成像的原理，现在给出一个数值仿真的例子。

假定目标面上同时存在两个点目标（5，2）和（2，-5）［见图12-11（a）］，取目标面倾角为φ=45°，转动角为9个值即θ=0，±5°，±10°，±15°，±20°，相当于目标面坐标转角γ=0°，±7.05°，±14.00°，±20.75°，±27.22°。因此在9个β（θ）投影轴上所得的一维积分函数如图12-11（b）所示。重构图像单独的反向投影只举例给出θ=0°［见图12-11（c）］，θ=20°［见图12-11（d）］和θ=-10°［见图12-11（e）］3种情况，图12-11（f）是最终的所有9个反向投影的非相干叠加合成的输出图像，其中两个反向投影线的交叉点即是成像点，与原目标点一致。进一步可以采用阈值处理等操作，消除投影线噪声，突出像点。

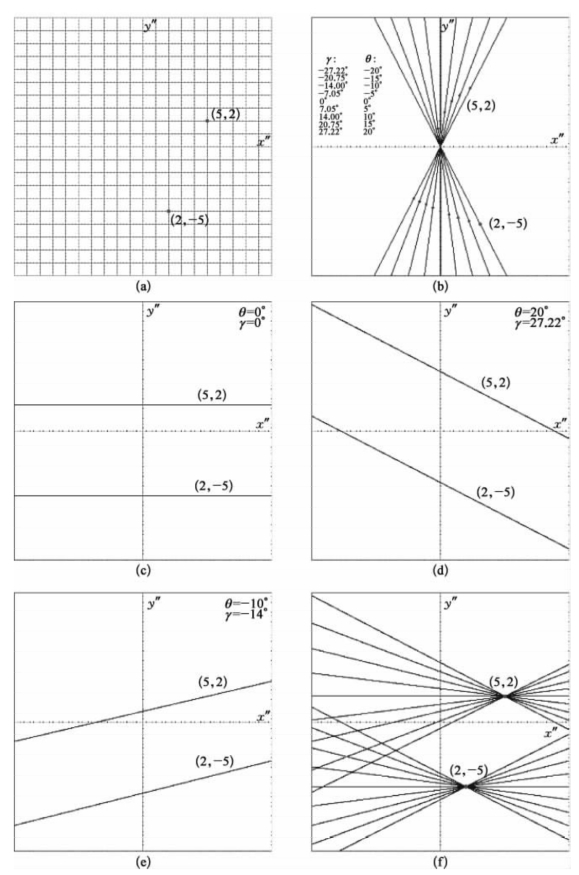
图12-11　非相干聚束SAIL距离分辨二维成像过程

（a）目标面上同时存在两个点目标点（5，2）和（2，-5）；（b）投影轴上所得的一维积分函数；（c）θ=0°下重构图像单独的反向投影；（d）θ=20°下重构图像单独的反向投影；（e）θ=-10°下重构图像单独的反向投影；（f）最终的所有9个反向投影的非相干叠加合成的输出图像

2）二维目标非相干处理多普勒频移分辨聚束模式

在层析聚束模式中，当目标快速转动时多普勒频移效应明显，这时可以采用单频连续激光测量多普勒频移，实现非相干处理多普勒频移分辨层析聚束模式。这时所得到的回波信号为多普勒频移，同样不需要时间相位信息。

设定目标旋转角速度为ω，由图12-10可见某一目标点（x″，y″）的旋转臂长为

相应的切向线速度为VL=Lω。因此在基准面法线方向（即观察方向）上激光光频的多普勒频移为

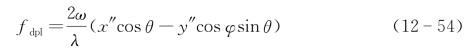
某一个多普勒频移fdpl：k的等位线方程为

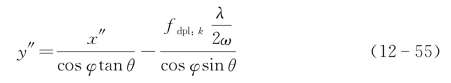
采用式（12-55）的同样坐标变换来定义投影轴方向，则当

(www.daowen.com)

某一次投影采样中目标点（x″，y″）对于基准平面的多普勒频移在投影轴上的位置为

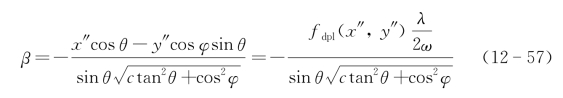
设目标函数p（x″，y″）为场强振幅分布，则沿多普勒频移等位线α方向上的多普勒分辨的图像函数在β轴上投影的积分为一维函数：

在距离分辨层析解调中采用的算法均可以应用于多普勒分辨层析解调，例如使用反向投影算法，目标像的计算公式为

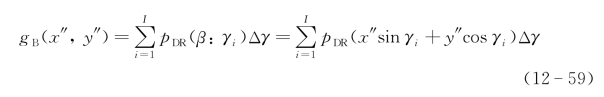
假定多普勒频移的测量精度为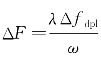，投影误差全宽度Δβ（θ）即为

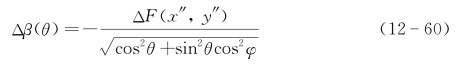
因此成像点最大值的直径为

而成像点函数最大边缘为

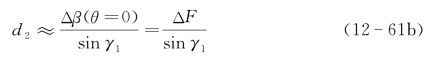
3）非相干处理聚束模式三维物体成像

三维成像的基本原理是基于上述的二维平面成像，可以把三维物体沿z轴并且平行基本目标面（x″，y″）作多剖面分解（见图12-12），各个剖面延长至旋转轴（y″）。然后同时对于各个剖面作非相干处理的距离分辨或者多普勒分辨的聚束模式成像，最后再合成三维图像。

对于第n距离剖面，相对于原点基准参考坐标系（x″（0），y″（0），z），三维物体可以采用距离剖面方式表达为

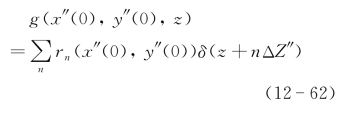
式中，rn（x″（0），y″（0））为在距离z=-nΔZ″上的物体所有存在的相关点的反射率，而剖面在z方向上的间隔为ΔZ″。剖面在y″上的面间隔为ΔY″，则有

定义第n距离剖面的坐标系为（x″（n），y″（n）），所有的距离剖面的旋转轴均在y″（0）上，由此该剖面的坐标中心在（x″（0）=0，y″（0）=nΔY″）。由此可知，第n距离剖面的坐标系（x″（n），y″（n））对于基准坐标系（x″（0），y″（0））的坐标变换为

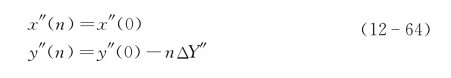
（1）三维目标的距离分辨三维和二维成像。

在距离分辨下，第n个距离剖面的距离方程为

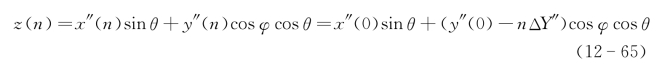
第n个距离剖面的目标函数为光强或者场强振幅分布r（x″（n），y″（n）），采用相同于式（12-65）的对于（α（n），β（n））的坐标变换，当转动角为

则第n距离剖面的某一个θ（γ）角的目标距离在β（n）轴上的一维投影为

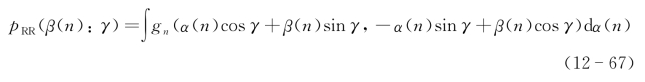
在剖面上同样可以采用上述各种层析解调，使用反向投影算法，第n距离剖面的目标像的计算公式为

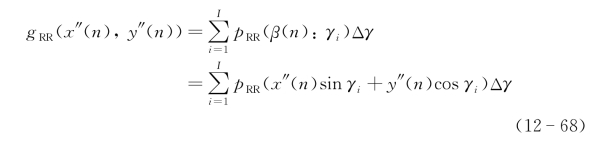
得到了所有距离剖面的目标二维像，则可以求得物体三维像为

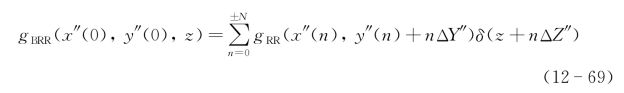
假定目标在y″方向宽度为Ly，由距离方程式（12-65）和坐标变换公式（12-64），在θ=0条件下可以求得两个相邻剖面的距离间隔为Lycosφ，为了保证距离剖面投影的积分在距离（时间）上不重叠，要求距离间隔满足条件：

如果三维成像所用的距离剖面的间隔远远达不到上述条件，将产生三维目标在深度方向压缩的距离分辨的二维像，具体操作时则不需进行分层，而只需作一次整体性的投影和解调。

（2）三维目标的多普勒频移二维压缩成像。

在多普勒频移分辨下，第n个距离剖面的多普勒频移方程为

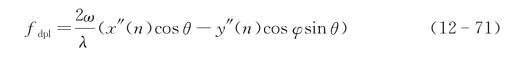
采用同样的（α（n），β（n））坐标变换即式（12-44），当转动角为

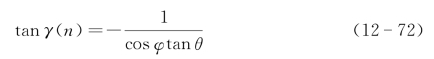
第n剖面的某一个θ（γ）角的目标多普勒频移在β（n）轴上投影的积分为一维函数：

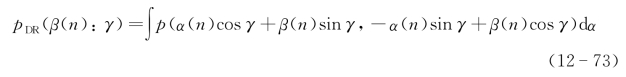
在剖面上同样可以采用上述各种层析解调，使用反向投影算法，第n剖面的目标像的计算公式为

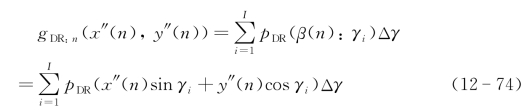
假定目标在x″方向宽度为Lx，由多普勒方程式（12-71）在θ=0条件下可以求得一个剖面的多普勒频移宽度为，而两个剖面之间的多普勒频移间隔近似为零，即fdpl：n+1（x″（n+1），y″（n+1））=fdpl：n（x″（n），y″（n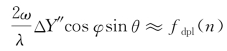））+。因此所有剖面的多普勒目标像不可能在剖面方向（z）上分辨出。所以在得到了所有剖面的目标像后，仅可能求得三维目标在z方向压缩的多普勒频移二维像：

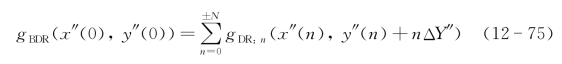
事实上具体操作时不需进行分层，而只需作一次整体性的投影和解调。

文献［35］的反射层析激光雷达的多普勒成像实验中，试验对象是具有倾角的旋转三维物体，事实上在原理上已经与该文献描述的方法有很大差别，严格意义上应当属于本节提出的多普勒分辨非相干处理聚束模式，即对于一个三维目标产生一个在深度压缩的多普勒频移二维图像。

应当注意，在多普勒频移成像下，数据收集时得到的多普勒频移投影不能分辨被测物体的剖面（剖线），因此重构像一般并不相似于原物体［35］，但是仍然具有目标的特征并可以用于目标识别。

4）相干处理聚束模式的层析原理解释

与采用点目标脉冲响应的分析方法对比［25，34］，下面给出聚束模式在相干处理时采用层析算法的数学分析。

相干处理的合成孔径激光成像雷达聚束模式采用脉冲啁啾激光和外差接收，解斜算法测量距离在交轨向成像，在顺轨向采用相干孔径合成，即相位二次项及其匹配滤波。上述相干处理的聚束模式也可以采用距离分辨CT层析算法结构，但是应当严格满足距离方向的时间测量相位同步关系和顺轨向的空间二次项相位关系。

这时在数据收集过程中，在满足严格的光频外差时间同步条件下，在目标点（x″，y″）上经受的相位历程为

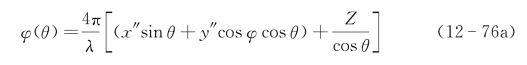
进一步近似并忽略常数，得到

式中，X为SAIL与目标的相对移动距离，Z为SAIL和目标面的中心距离，事实上X=Zθ。

目标函数为场强振幅分布p（x″，y″），则在交轨向聚焦后在距离等位线α方向上的距离分辨的图像函数投影的积分为一维函数：

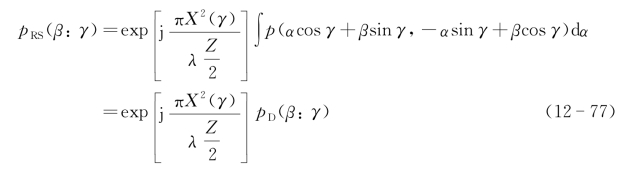
然后在图像处理中采用空间二次项相位匹配的反向投影算法（或者上述其他算法），目标像的计算公式为

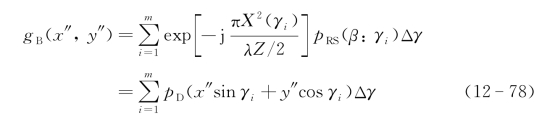
式中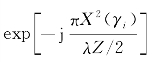，为匹配滤波器相位函数。

上述采用层析算法的相干处理聚束模式的分析结果与采用点目标脉冲响应［25，34］的分析结果是一致的。应当注意，聚束模式在微波合成孔径雷达中的空间相位历程是恒值，二次项（即波前曲率）的存在是作为像点扩散而降低成像质量的重要原因［32］。而对于激光合成孔径雷达，在数据收集过程中产生精确的空间二次项相位是顺轨向相干合成的必要条件。

如上所述，聚束相干SAIL比聚束非相干SAIL具有更好的成像分辨率，同时也明显可见具有更高的信噪比，因为对于N个信号相干叠加的信噪比为N2，而非相干叠加的信噪比为N。

本节根据计算机层析术的投影成像原理，提出了非相干合成孔径激光成像雷达的概念和方法，特点是硬件结构简单，对于光频的空间相位分布和频率时间相位同步无严格要求，因此极大地降低了信号收集和数据处理中的技术难度，但是成像分辨率和信噪比原理上低于相干SAIL。

本节的非相干SAIL具有操作的多样性：能提供3种工作模式（传统的聚束模式、逆聚束模式和成像聚束模式）；包括两种传感成像方式（距离分辨成像和多普勒频移成像）；多种维度变换成像的可能性，主要适用于平面目标的二维距离分辨和多普勒分辨成像，也可以实施三维物体的距离分辨三维层析以及深度压缩的距离分辨和多普勒频移分辨二维成像。其中对于一个三维目标产生深度压缩的二维距离分辨或多普勒频移分辨成像更是一个有用的概念。应当注意到相干SAIL很难实现聚束模式，在相对运动中保持远低于厘米数量级成像分辨率的光学足趾指向精度是极其困难的。

本方法在原理上也包含了用于目标轮廓成像的反射层析激光成像雷达，在数学上使φ=0，则距离分辨成像公式和多普勒频移成像公式都可以简化到反射层析激光成像雷达的成像表达式［35］。