合成孔径激光成像雷达具有小视场高分辨的特点，陀螺稳定平台所不能补偿的高频姿态扰动残差将明显影响激光合成孔径成像，算法上需要根据POS记录的姿态数据进行补偿成像。由于POS记录的纬度、经度、高度数据基于地理坐标系，而姿态角度数据基于大地坐标系，因此需要将POS数据转化到雷达本体坐标系进行算法补偿。

地球坐标系（见图11-55）：原点取在地心，x为赤道平面与本初子午线的交线，z与地球自转轴重合，与xy组成的平面垂直，y轴符合右手螺旋定则。显然地球坐标系与地球固连，并与地球一起转动。

导航定位中常用经、纬度表示载体相对于地球表面的位置。

地理坐标系（见图11-55）：以地球作为参照系时，规定：原点O——飞行器重心在地球表面的投影点；E轴（X轴）——指东，即坐标原点纬线向东的切线；N轴（Y轴）——指北，即坐标原点经线向北的切线；Z轴——沿地垂线方向，指向天空。

机体坐标系（见图11-56）：机体坐标系与飞机固连，坐标原点与飞机重心重合，z与飞机纵轴一致，y与飞机竖轴一致，x与飞机横轴一致。将沿y轴的旋转定义为翻滚，沿x轴的旋转定义为俯仰，沿z轴的旋转定义为偏航。

大地坐标系：大地坐标系是大地测量的基本坐标系，其大地经度L、大地纬度B和大地高H为此坐标系的3个坐标分量。其地面上一点的大地经度L为大地起始子午面与该点所在的子午面所构成的二面角，由起始子午面起算，向东为正，称为东经（0～180），向西为负，称为西经（0～180）；大地纬度B是经过该点作椭球面的法线与赤道面的夹角，由赤道面起算，向北为正，称为北纬（0～90），向南为负，称为南纬（0～90）；大地高H是地面点沿椭球的法线到椭球面的距离。

1）将大地坐标系转换到地球坐标系（见图11-57）

由GPS获得的经度（λ）、纬度（φ）、高度（h）信息（大地坐标系）可以转化到地球坐标系，由世界大地系WGS84（或者大地参考系GRS80），可知地球赤道横截面半径a为6 378.137 km，地轴横截面的半径b为6 356.7523142 km，因此椭圆的偏心率e可以由下式确定：

WGS 84中e2=0.006 694 379 990 14，GRS 80中e2=0.00669438002290，两者非常接近，b只差0.1 mm。

由下式可以将经纬度信息转化到笛卡儿地球坐标系：

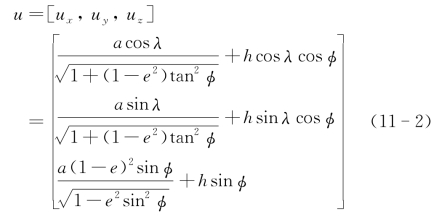
2）将地球坐标系中心平移至以雷达为圆心

由GPS得到飞机的坐标信息（φ1，λ1，h1），同样由GPS得到靶点信息（φ2，λ2，h2）。

将飞机与靶点坐标信息转换到地球坐标系：

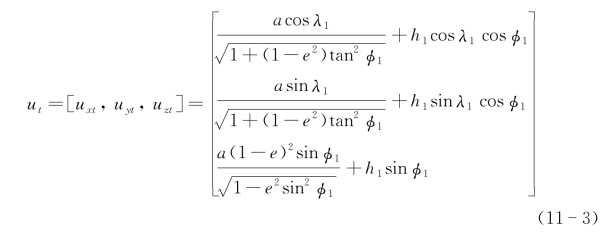
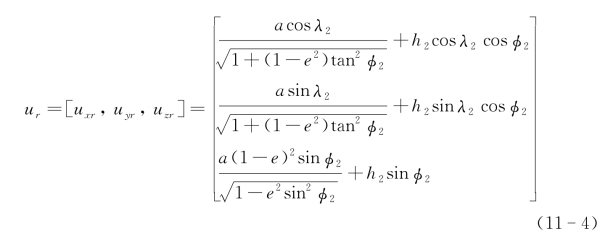
以靶点为原点O，则飞机质心在地球坐标系的相对坐标为

3）相对坐标系转化至雷达本体坐标系

（1）飞机姿态改变导致雷达本体坐标系的改变。

飞机的起始位置与转化后的地球坐标系的原点重合，此时，定义为O1，机体坐标系的3轴与地理坐标系的3轴重合，飞机与地理坐标系Y轴的夹角定义为偏航角。随着飞机的飞行，靶点与飞机的相对位置发生变化，再加上飞机姿态的改变，最终导致靶点在雷达本体坐标系中的位置发生变化。

由于飞机姿态的变换，导致机体坐标系的变化，机体坐标系的变化又直接影响靶点在机体坐标系的变化。

如图11-58所示，

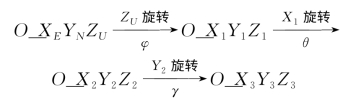
各次基本旋转对应的变换矩阵为

所以，姿态矩阵为

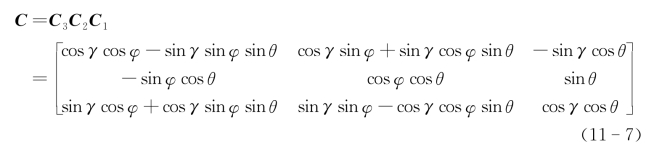
（2）靶点的位置在飞机坐标系中的坐标。

由姿态改变矩阵可以知道：φ=90°+λ，θ=90°-φ，γ=0°，则将靶点的位置转换到以飞机质心为原点的地理坐标系中的坐标为(www.daowen.com)

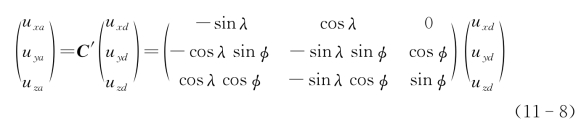
再由此地理坐标系经过姿态变化矩阵，转移到雷达本体坐标系得到靶点在雷达本体坐标系的位置：

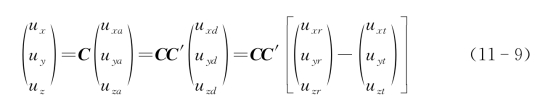
雷达回波信号可以表示为

式中，xp，yp为靶点的位置，α=a／M，a为振镜振动角度的振幅，M为放大倍率，l为光斑距离振镜中心的距离，即调制长度；β为飞机飞行速度。

由转换方程式（11-8）和式（11-9）可知，理想情况下的转换为

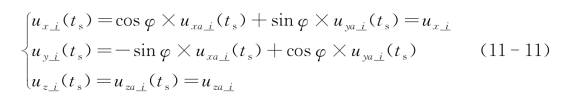
φ为航向，uxa＿i，uya＿i，uza＿i为理想情况下，飞机在以靶点为质心的地理坐标系下的坐标，ux＿i，uy＿i，uz＿i即为在雷达本体坐标系中的坐标。

真实情况下，飞机飞行存在平移和姿态变化，其中，平移主要体现在飞机的飞行轨迹上，即，经纬度的偏移：

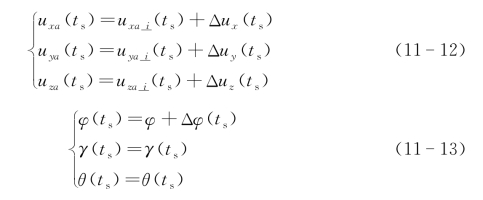
由转化矩阵：

假设俯仰与翻滚角度很小（振幅一般在0.1°以下），此时当姿态随时间变化时：

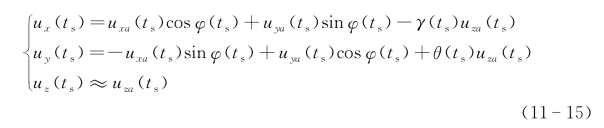
理想的飞行状态下，γ=0，θ=0，φ为定值。

由式（11-15）可知，

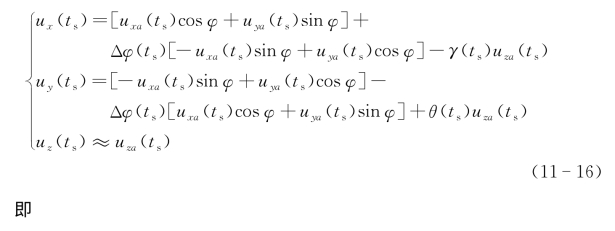
由式（11-18）可以看出，由于Δux（ts），Δuy（ts）仅与雷达与靶点的理论方位角和靶点的位置偏差有关，与具体的位置无关，因此，此误差属于非空变误差。同时，γ（ts）uza（ts）与θ（ts）uza（ts）亦属于非空变误差。因此，对采样数据首先进行非空变误差补偿。

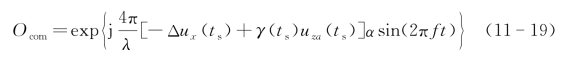
然后，对交轨向空变误差的补偿采取逐点补偿。方法如下：

一个顺轨向点（ts1）上，以它为中心选取一个合成孔径长度，交轨向补偿方程为

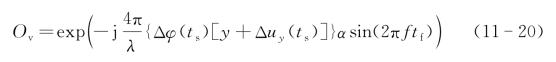
同时，顺轨向因为同样存在空变误差，顾同样采取逐点补偿的方式，补偿函数为

式中，为成像区x值，k交轨向经过插值后的斜率。

经过上述补偿，最终得到ts1此时刻的成像数据，然后对下一个顺轨向位置进行补偿，直到完成整个匹配。

3 km高度原始数据不经过任何处理，直接交轨向FFT压缩的结果如图11-59所示，可见明显的相位非线性调制造成的混叠。经过交轨非线性差值算法补偿后如图11-60所示，单个字母信号轨迹明显可见，弯曲显示雷达系统存在陀螺稳定平台无法完全补偿的角度扰动。

根据上述算法，利用POS数据补偿交轨方向的角度扰动，即滚动角度残差，顺轨向数据拉直如图11-61所示。

用理论二次项直接作匹配滤波的二维成像结果如图11-62所示，可见俯仰角度扰动和非匀速飞行造成分辨率下降，经过POS数据补偿后二维成像结果如图11-63所示，分辨率明显提高，提升了方位分辨率。