一个成像分辨率单元的成像场强或者成像光强是与光学接收口径对于散斑尺寸之比及其在合成孔径长度上的积分大小密切相关，其中孔径合成长度就是接收天线散斑孔径积分光场相干函数或者光强相干函数确定的相干长度。当然不同结构的SAIL（如啁啾调制SAIL、伪随机相位编码调制SAIL和直视SAIL），由于原理不同它们的散斑效应影响的程度也有很大的差别。总之，不同的成像分辨率单元上的光场或者光强变化愈大，则散斑效应愈明显。本节将在局域理想散斑条件下研究一个目标分辨率单元成像点的强度起伏分布特性，因为强度起伏能够直接表征散斑效应的程度，起伏愈大则散斑效应愈明显。

首先定义局域理想散斑状态为在空间小范围内散斑可以认为具有以平均宽度为半周期的周期性黑白光强分布，同时在散斑内具有相同的相位分布。定义顺轨向功率积分来表达成像单元的散斑效应大小：

式中，S（α，β）为最理想化的局域散斑分布函数，A（x，y）为接收孔径函数，Sy是最理想化散斑的顺轨向平均宽度，NSy为等效于合成孔径长度的积分长度，N≥1，而y0为积分起点，不同取值下的积分功率变化大小就代表了散斑效应的强弱，显然它的取其变化范围应当为0≤y0≤2Sy或者相当范围。

为了采用顺轨向积分功率来比较散斑效应影响的大小，定义如下参考因子：

（1）顺轨向积分接收功率的波动度。在一个散斑周期长度范围内的积分功率的起伏显然能够表征散斑效应的影响，因此在数值上定义一个散斑周期内的波动度来代表功率起伏。

对于伪随机相位编码侧视SAIL和直视SAIL，波动度定义为

对于啁啾侧视SAIL，交轨向啁啾造成的交轨向散斑移动，为

式中，取平方运算因为考虑了交轨向光频啁啾散斑运动引起的双重散斑效应。

可见波纹度数值愈小则散斑影响愈小，波纹度数值愈大则散斑影响愈强。当顺轨向积分功率具有零值时，波纹度为1。

（2）顺轨向积分接收功率的零值占据比。在一个散斑周期长度范围内的顺轨向积分功率可能具有的功率零值的占据比，也能够反映散斑效应的影响程度，即

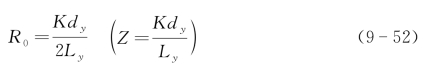
式中，K为零点数。可见零值占据比愈大，散斑效应影响愈强。

（3）顺轨向积分接收功率的相对等效合成孔径尺度。在一个散斑周期长度范围内，定义功率下降到0.5的归一化顺轨向长度为相对等效孔径合成尺度，即(www.daowen.com)

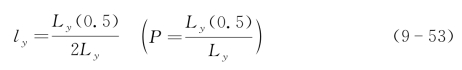
其中，Ly（0.5）为功率下降到0.5的顺轨向长度。可见相对等效合成孔径尺度接近于1时，散斑效应影响最小。

侧视SAIL和直视SAIL的散斑效应比较如下：

（1）直视SAIL。

在矩形孔径条件下，计算了在不同初始积分位置（-Ly≤y0≤Ly）下的接收功率波动度（V）、接收功率零值占据比（R0）和等效合成孔径尺度（ly）与设计孔径合成长度（N=1～6）的关系。结果如图9-11所示。

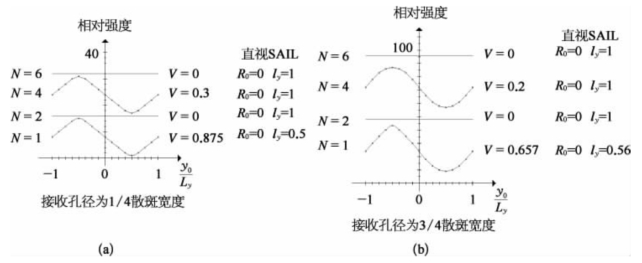
图9-11　直视SAIL在不同初始积分位置（y0）下的接收功率波动度（V）、接收功率零值占据比（R0）、等效合成孔径尺度（ly）与设计孔径合成长度（N）的关系

（a）接收孔径为散斑平均宽度的1／4；（b）接收孔径为散斑平均宽度的3／4

在接收孔径为1／4散斑宽度和3／4散斑宽度下可见：积分接收功率波动度较小，随着孔径合成长度（N）增加，积分接收功率波动度趋向零；不存在积分功率为零值的顺轨向占据位置；超过1个散斑周期孔径合成长度（N=1）时等效合成孔径长度等于设计合成孔径长度。同时可见接收孔径增大时散斑影响更小。由此可以得出结论：直视SAIL散斑效应影响较弱，接收孔径愈大则散斑影响愈小，其中顺轨向孔径合成长度愈大则散斑影响愈小。

（2）侧视SAIL。

图9-12　侧视SAIL在不同初始积分位置（y0）下的接收功率波动度（V）、接收功率零值占据比（R0）、等效合成孔径尺度（ly）与设计孔径合成长度（N）的关系

（a）接收孔径为散斑平均宽度的1／4；（b）接收孔径为散斑平均宽度的3／4

如图9-13所示，在接收孔径为1／4散斑宽度和3／4散斑宽度下可见：积分接收功率波动度很大（V=1），明显存在积分功率为零值的顺轨向占据位置；因为散斑孔径积分场复相干函数在顺轨向孔径合成长度只能限制于一个散斑周期（N=1）之内，这时等效合成孔径长度远小于设计合成孔径长度。同时可见接收孔径增大时散斑影响略有改善。由此可以得出结论：侧视SAIL散斑效应影响明显，同时也可以看到交轨向啁啾激光光频距离分辨方法比激光内脉冲调制距离分辨方法的散斑影响更强烈，这是由于交轨向存在散斑移动的缘故。

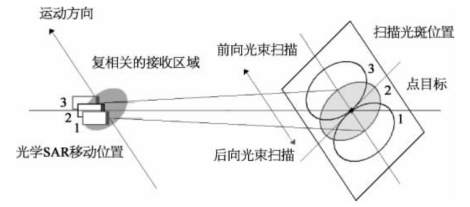
图9-13　滑动聚束模式