一个成像分辨率单元的成像场强或者成像光强是与光学接收口径对于散斑尺寸之比及其在合成孔径长度上的积分大小密切有关，其中孔径合成长度就是接收天线散斑孔径积分光场相干函数或者光强相干函数确定的相干长度。不同的成像分辨率单元上的光场或者光强变化愈大，则散斑效应愈明显。

1）侧视啁啾SAIL散斑效应分析

侧视SAIL采用光学外差探测，光学天线接收孔径函数为w（x，y）=rect（x／D）rect（y／D），而目标垂直参考面上的分辨单元孔径为rect（x／d）rect（y／d），对于一个相对可移动光学天线其激光散斑光电流为（π桥接器两路）

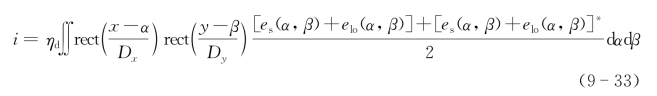
取单一交流通道输出为

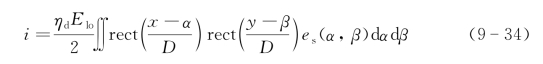
事实上，其中积分部分相当于光学接收天线的散斑孔径积分场。

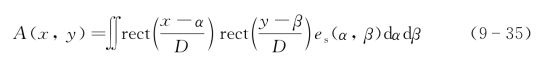
因此，归一化光学接收天线散斑孔径积分场复相干系数可以描述光学天线孔径相对于散斑场移动时所持有的相干度，即孔径合成的可能性：

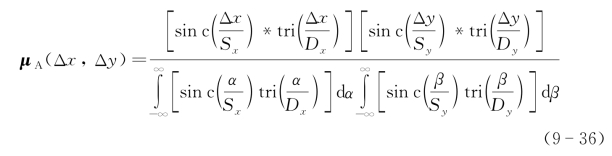
天线孔径相对运动包括快时间上的光斑啁啾引起的交轨向移动和顺轨向上孔径合成所需要的移动。

如9.2.4节所述，其宽度等同于两倍散斑平均宽度。其中Sx=λZ／ΔSx，。这里定义天线散斑孔径积分场复相干系数的宽度为其峰值两侧零点（或者最小值）之间的宽度（W），而散斑复相关因子的宽度为Ws，x=2λZ／ΔSx，，即两倍散斑平均尺寸，天线孔径函数的自相关函数宽度为Wa，x=2Lx，Wa，y=2Ly，即两倍天线孔径宽度。

假设发射光学和接收光学均具有相同的方形孔径：

衍射光斑和光学外差接收方向性函数即光学足趾的零值全宽带为

这也是孔径合成的长度，其理想零值全宽成像分辨率为

目标分辨率单元产生的回波接收面散斑平均尺寸为

可见，散斑平均尺寸与光学足趾尺寸相同。因此，散斑平均尺寸也就是顺轨向孔径合成长度，同样也是激光啁啾在交轨向移动的距离。为分析简单，假定在最理想的局域状态下散斑按平均宽度周期分布，在孔径合成过程中光学孔径先在交轨向移动一个散斑平均宽度，然后依次沿顺轨向运动一个散斑平均宽度，如图9-9所示。

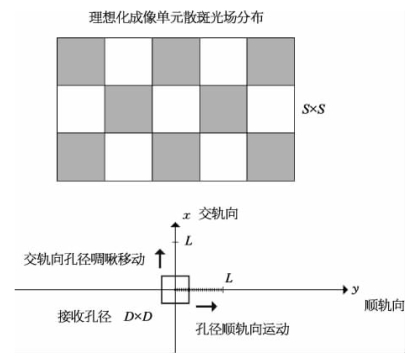
图9-9　理想化成像单元散斑光场分布

定义光学孔径相对于散斑平均宽度之比为覆盖率：

(www.daowen.com)

这一过程中，由于相邻一个间隔的两个散斑之间并不存在任何相关性，只有一个散斑内具有相关性，因此光学孔径大于散斑平均宽度是没有意义的。我们考虑覆盖率的几个极限情况来表示散斑的影响。

当光学孔径远远小于散斑平均宽度时，顺轨向时间起点落在散斑黑白一个周期中的任何位置的可能性是均等的。

当成像分辨率、波长和作用距离分别为d=1 cm，λ=10-6m，Z=3 km，且光学收发系统的孔径为D=2 cm时，光学足趾宽带和散斑平均宽度为

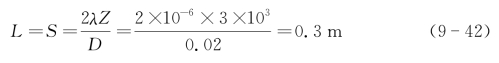
可见收发孔径相对于散斑平均宽度的覆盖率为

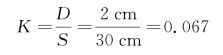
而成像单元数为

2）直视啁啾SAIL散斑效应分析

直视SAIL采用光学自差探测，对于一个相对可移动光学天线其激光散斑光电流为（π-桥接器两路）

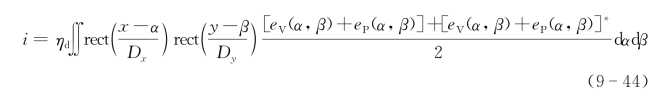
取单一交流通道输出为强度积分

因此光学接收天线的散斑孔径积分场的归一化强度相干函数可以描述光学天线孔径相对于散斑场移动时所持有的相干度，即孔径合成的可能性。图9-10为理想化成像单元散斑光强分布。

图9-10　理想化成像单元散斑光场分布

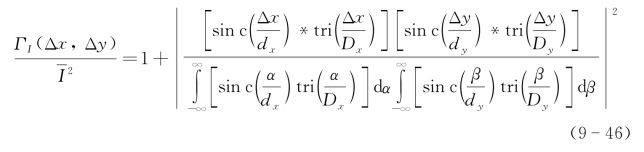
3）接收天线散斑孔径积分场复相干系数应用于顺轨向和交轨向成像

合成孔径激光成像雷达的交轨向成像采用啁啾激光的距离分辨实现，顺轨向成像采用二次项历程的孔径合成实现。顺轨向（x方向）的成像过程可以采用散斑孔径积分场复相干系数进行分析和设计，这时可以仅考虑x方向。假设发射孔径为dx，则目标面上的激光照明光斑的宽度为Dx=2λZ／dx，因此成像分辨单元尺寸为ΔSx=dx／2。考虑实际使用的孔径合成尺度对于激光照明光斑宽度的比为Ksyn（Ksyn≤1），这时成像分辨单元尺寸为ΔSx=dx／（2Ksyn），其产生的散斑尺寸为Sx=2KsynλZ／dx。接收天线的孔径宽度为Lx=KRTdx，应当注意由于外差接收的方向性函数决定于接收口径，为了得到较大的外差接收口径必须采用多通道等特殊结构［5～8］。因此在接收面接收天线口径对于目标分辨单元散斑平均尺寸的比为

SAIL总体方案的设计一般要求有足够大的照明光斑，因此激光发射口径较小。虽然要求很高的成像分辨率但是分辨单元尺度还是大于发射口径，因此必须设计一定的Ksyn值。为了保证足够的回波接收能量，要求有较大的KRT值。在均衡的考虑下一般可以达到K≤1，散斑尺寸大于等于接收天线尺寸，孔径合成长度为二倍散斑宽度，可以控制适当大的散斑长度以产生比较长的合成孔径长度，SAIL处于较合理的散斑抑制状态。如果K＞1、接收天线尺寸大于散斑尺寸，这时孔径合成长度为二倍天线宽度。由于光学天线的尺度限制，使用较大的接收天线产生比较长的合成孔径长度很困难，而且这种情况下顺轨向的成像分辨率比很低。

在快时间轴记录啁啾激光的距离信息回波时，由于啁啾造成的激光连续波长变化可能产生散斑的空间时间变化［12］，一个具有倾斜角的目标分辨单元在啁啾范围产生交轨向附加相移的最大波长数为2，等同于在交轨向y轴引入了一个线性相位移，其最大值为2π（2λ／Ly）y，在傅里叶变换后相当于产生一个连续位置偏移，最大值为

一般而言，啁啾的波长变化在一个成像分辨单元内不会引起散射相延的明显变化，因此在一个啁啾周期内在接收面上的激光散斑可能在交轨向移动了距离Pmax，即在天线散斑孔径积分场复相干系数中相当于散斑函数在交轨向坐标上移动了Pmax。如果散斑宽度远大于天线宽度而天线散斑孔径积分场复相干系数由散斑复相干因子确定，这时目标分辨单元的外差差频信号的宽度刚好占据了一个相干宽度W=Pmax，这种情况下造成差频信号的振幅和相位波动，可以观察到回波强度可能存在一个周期的不均匀性。如果天线宽度远远大于散斑宽度而天线积分场复相干系数由天线孔径三角函数确定，比较容易做到Wy≫Pmax，即在差频信号的宽度内基本满足相干性，回波强度在一个周期内比较均匀。

在系统总体设计上可见，在顺轨向应选散斑长度较大，而在交轨向应选天线长度较大。同时接收天线散斑孔径积分场复相干系数的宽度在顺轨向和交轨向均存在矛盾，需要仔细考虑。