在光学天线孔径内接收的光场积分称为天线接收场，它与光学外差探测光电流有关。SAIL成像中有两个与接收场积分有密切关系的核心问题。一是SAIL在顺轨向移动中接收场积分的振幅特别是相位能够维持多少距离的稳定或者平稳变化，这个距离与孔径合成长度定义有关。二是在交轨向信号快时间接收过程中是否存在光学天线在交轨向移动的可能，这会影响顺轨向初始相位的稳定和交轨向聚焦，例如啁啾侧视SAIL，光频啁啾将导致散斑的空间时间变化。

回波光学外差产生的差频光电流信号的振幅和相位能够维持多少时间的稳定或平稳变化，这与散斑最大移动距离和孔径合成长度均有关。定义天线移动产生的积分接收场的复相干系数来求解上述问题。包括接收天线散斑场积分的复数相干函数和强度相干函数。

光学接收天线散斑孔径积分光场相关函数及其复相干系数定义为在接收面上以一定的接收口径整体采样的散斑场的自相关函数［4］，即这个积分场移动时能够与原来位置的积分光场保持相干的程度。

1）光学接收天线散斑孔径积分光场相干函数

令ΓA=JA为接收面上散斑孔径积分光场的自相关函数，则从接收面的光场自相干函数ΓS=JS可以求得在孔径a（x，y）内的积分光场相关函数。

首先建立目标表面散射场与位移天线接收场之间的相干场关系，在夫琅禾费远场衍射下接收面光场与目标函数的关系为

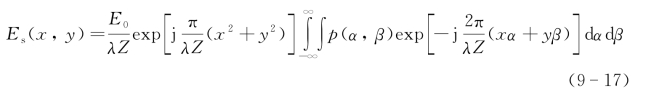
同样p（α，β）为归一化目标函数，忽略第一项相位二次项。令光学天线孔径函数为a（x，y），则位移天线的接收积分光场为

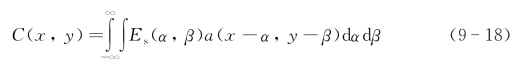
进一步推导可表示为

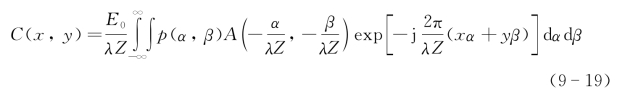
式中，

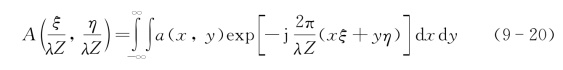
定义漫散射目标的互强度为

则从C（x，y）的表达式可以得到散斑效应的互强度传递为

式中，x2=x1+Δx，y2=y1+Δy，通过运算接收面上的光场相关函数为散斑复相关因子和天线孔径自相关函数的卷积，即

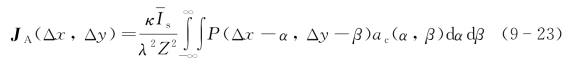
与目标单元产生的散斑尺度有关的散斑复相关因子为

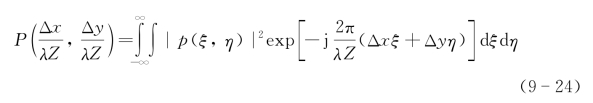
已知孔径函数的复自相关函数为

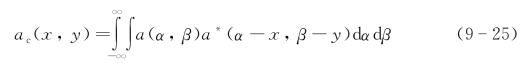
因为

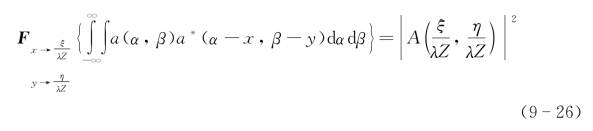(www.daowen.com)

所以上述与光学天线尺度有关的天线孔径函数的自相关函数为

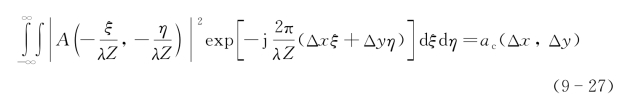
因此，定义归一化光学接收天线散斑孔径积分光场相干函数即复相干系数为

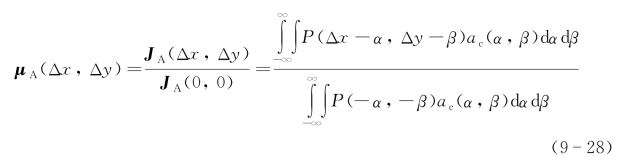
2）光学接收天线散斑孔径积分光强度相干函数

已知接收天线散斑孔径积分场的复相干系数，可以得到其强度分布的相关函数［5］，天线散斑孔径积分光强光相关函数为

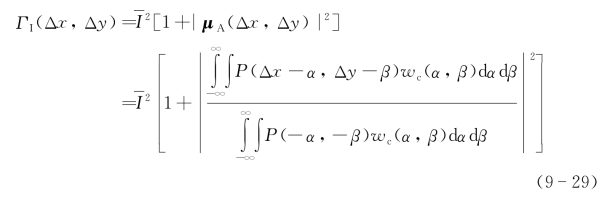
式中，为光强平均值平方，。

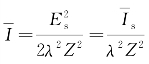光学接收天线散斑孔径积分归一化光强相干函数为

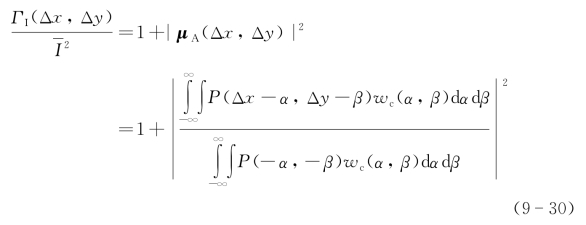
可以看出，在相同的复相干系数下，积分光场相干函数正比于该复相干系数，而积分光强相干函数具有一个相当于0.5归一化度的背景，具有整体相干性。应当注意，接收天线孔径积分场的散斑强度相干函数是一个带有中心峰值和具有最大值一半的恒定值背景所组成的分布，在很大范围内具有较高的相干度。而接收天线孔径散斑积分场的复相干系数是一种中心峰值的分布，相干范围仅在中心附近。可见直视SAIL中，由于敏感于光强而自然消除了随机的相位分布，散斑的天线积分光强的相干性远远高于侧视SAIL。

3）矩形成像分辨率单元和矩形天线孔径的复相干系数分析比较

为解释其物理意义，可以采用一个方形函数来进行简单分析，设计接收孔径为Dx×Dy，即w（x，y）=rect（x／Dx）rect（y／Dy）；目标垂直参考面上的分辨单元尺寸为dx×dy，即rect（x／dx）rect（y／dy）；散斑宽度为Sx×Sy，有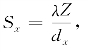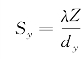。则二维分离变量的光学接收天线的散斑孔径积分场复相干系数为

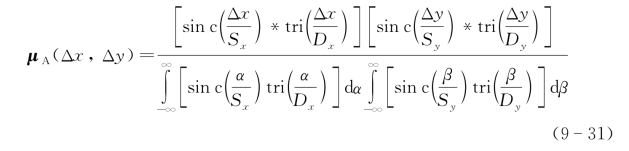
式中，

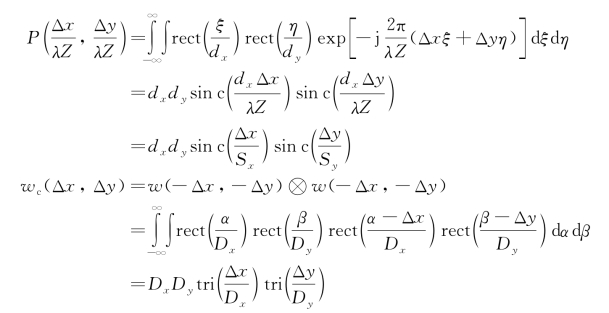
对于方形函数，有D=Dx=Dy，d=dx=dy和S=Sx=Sy，因此复相干系数为

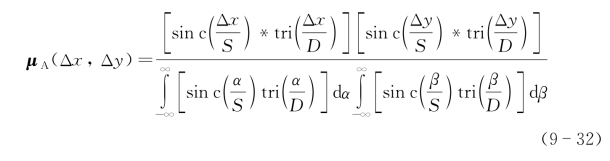
图9-7给出了在不同宽度的矩形天线自相关函数和矩形分辨单元散斑自相关函数下的归一化坐标的归一化一维天线散斑孔径积分场复相干系数，令天线自相关函数宽度对于散斑复相关因子宽度的比即接收面接收天线口径对于目标分辨单元散斑平均尺寸的比为K=Wa／Ws=L／S。图中可以看出存在如下趋势：①当天线自相关函数宽度远大于散斑复相关因子宽度即K≫1时，散斑积分场复相干系数的宽度由天线孔径三角函数宽度确定即W≈Wa，即为天线二倍宽度即Wx=2Lx；②当散斑复相关因子宽度远大于天线自相关函数宽度即K≪1时，散斑积分场复相干系数的宽度由散斑复相关因子宽度确定即W≈Ws，即为二倍散斑宽度即Wx=2λZ／ΔSx；③当天线自相关函数宽度与散斑复相关因子宽度相当即K≈1时，散斑积分场复相干系数的宽度近似等于二倍天线自相关函数宽度或者二倍散斑复相关因子宽度即Wx≈2Lx≈2λZ／ΔSx。

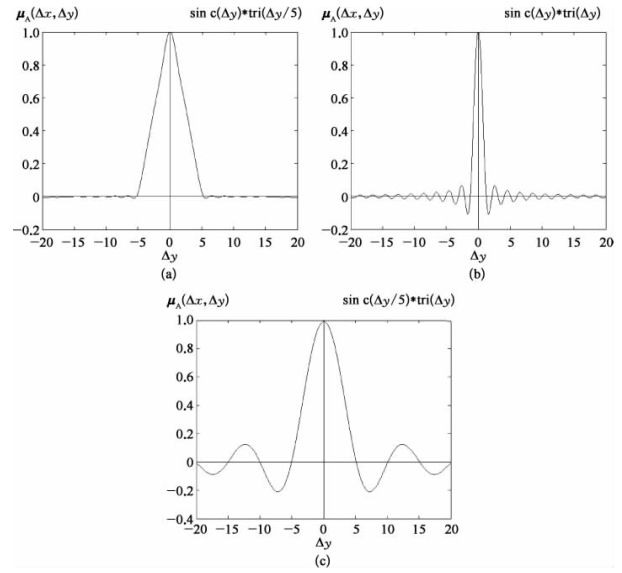
图9-7　归一化坐标下的归一化一维接收天线散斑孔径积分场复相干系数

天线孔径三角函数宽度与散斑分布函数之比为：（a）5∶1；（b）1∶1；（c）1∶5

图9-8为天线孔径三角函数宽度与散斑分布函数之比为1∶1情况下的散斑孔径积分光场复相干系数和散斑孔径积分光强自相关函数的比较，可以看出光强自相关函数具有很宽范围的相干度（归一化0.5）。

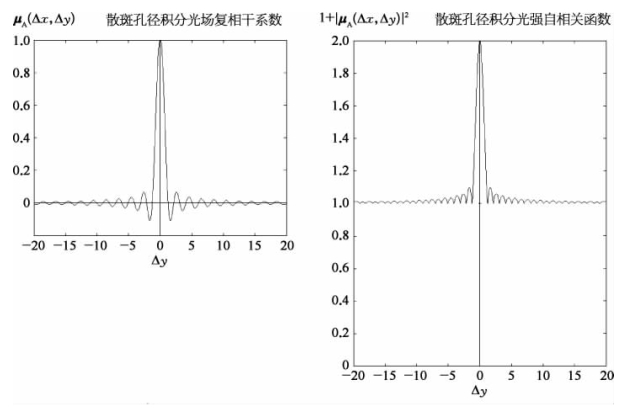
图9-8　散斑孔径积分光场复相干系数（左）与散斑孔径积分光强自相关函数（右）