一个漫反射表面对于照射激光的反射，经过自由空间传播在观察面上将产生激光散斑。在合成孔径激光成像雷达的接收面上的光场是整个目标的漫反射场的线性叠加，目标由成像分辨单元组成，因此对于漫反射目标，它产生的散斑效应可以用目标面上一个成像分辨单元来分析，这与SAIL的二维数据收集和成像处理过程采用成像分辨单元来分析是一样的原理。SAIL涉及的散斑具有自身独特的特性，下面先分析相关的基础性SAIL散斑效应。

假定在本章分析中漫反射物体是偏振理想的，即散斑是偏振的，即该物体表面反射是保偏的，同时在正交偏振态入射下其散斑图形是不变的，例如粗糙的金属表面具有这种散斑偏振特性。

1）合成孔径激光成像雷达散斑的光场和光强相干特性

一个成像分辨单元通过自由空间传播在接收面上产生散斑的过程如图9-2所示。激光散斑最基本的统计性质是其花样的平均尺寸，这可以由散斑光强自相关函数给出。由于准单色条件下互强度与光场自相关函数一致，因此可以由激光散斑复相关因子和散斑光强自相关函数求得漫反射目标在接收面上的大散斑平均尺寸［1］。

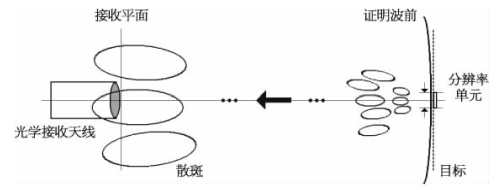
图9-2　激光散斑产生示意图

一个场强分布函数为p（ξ，η）的激光散射源（即SAIL成像分辨单元）在距离Z上产生的散斑光强自相关函数可以采用如下过程求得。

空间非相干光源的互强度为ξ2，η1-η2），因此在接收面上产生的互强度为

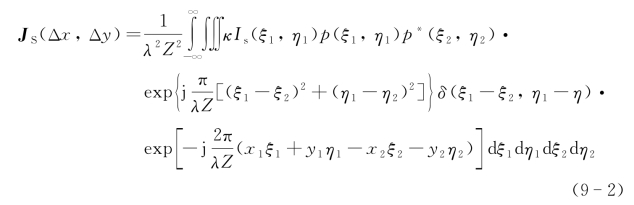
可以认为平均光强为I0，而p（x，y）为归一化光场函数。可以推导得到接收面上散斑场的互强度为

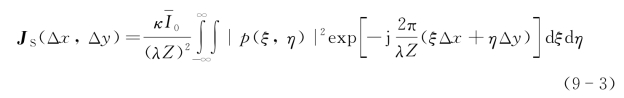
式中Δx=x1-x2，Δy=y1-y2。因此散斑复相关因子为

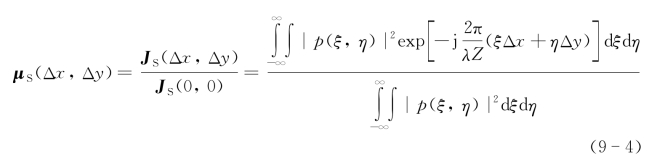
而散斑光强自相关函数为

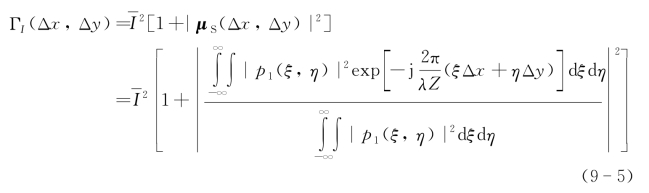
因此，散斑光强的功率谱密度函数为

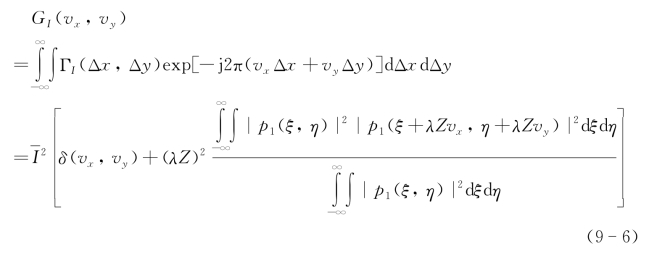
式中，x，Δx，ξ为交轨向坐标，y，Δy，η为顺轨向坐标，I 为散斑平均光强，λ为波长。

应当注意矩形孔径下的SAIL具有最好的成像分辨率［13］，因此本节分析举例中均采用矩形孔径，但是其结果也很容易推广到圆形等其他孔径。(www.daowen.com)

2）激光散斑的平均尺度

目标面上的一个原始矩形单元dx×dy，在SAIL接收面上散斑的平均宽度为

相当于dx×dy的衍射花样的半高全宽。此外，采用等当面积方法可以得到相同的结果。

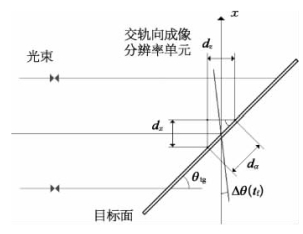
图9-3　目标一个分辨单元上波长变化产生的相位延时变化

因此两倍平均宽度可以认为是包含一个最大光强和一个最小光强的一个散斑周期，也可以看到散斑的归一化复相关因子的零值全宽度等同于两倍散斑平均宽度。对于目标面上的一个初始矩形成像分辨单元为dz×dy，初始交轨向成像分辨率dz直接由距离分辨z方向的测定而定，应当注意SAIL的观察面具有一定角度θtg（见图9-3），因此交轨向分辨率也可以表达在坐标系的x方向即dx或者目标斜面的α方向即dα，它们的关系是

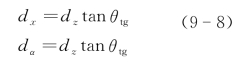
对于目标面上的一个原始矩形成像分辨单元dz×dy，在垂直于系统主轴的主面上的投影为矩孔tanθtgdz×dy，可以近似认为斜面正方单元和矩形窗口具有相同的散射统计特性，因此SAIL接收面上散斑的平均宽度为

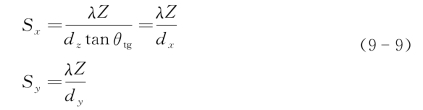
一般设计中，取Sx=Sy，则有dy=dx=dztanθtg。

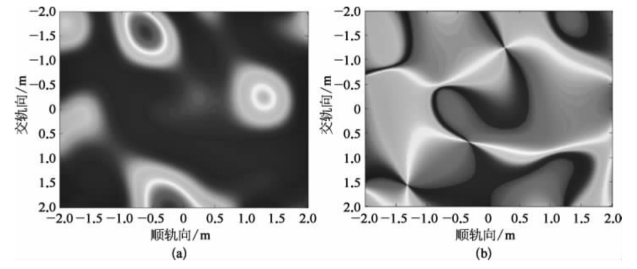
图9-4　脉冲初始端波长λ0＝1 550.514 9 nm的散斑

（a）振幅图样；（b）相位分布

图9-4（a）是模拟散斑强度的图样，呈现亮暗相间的颗粒状分布。其中，dx=5 cm，dy=3.53 cm，Z=30 km，通过式（9-9）可以求出散斑花样在交轨向上的平均宽度为Sy=1.315 m，在顺轨向上的平均宽度为Sx=0.93 m。图9-4（b）是散斑相位分布，图中相位突变点的位置与图9-4（a）中散斑强度零值所在位置一致。由相位突变点划分出的相位变化区域也和散斑图样的强度起伏区域类似。文献［2］指出散斑强度零值处，散斑光场的实部与虚部都为0，相位是任意的，但是可以观察到在其附近相位呈现涡旋分布。图9-5（a）是散斑等强度线图，图中散斑强度变化剧烈区域对应图9-5（b）中相位突变点，散斑个数与相位突变点个数大致相同。

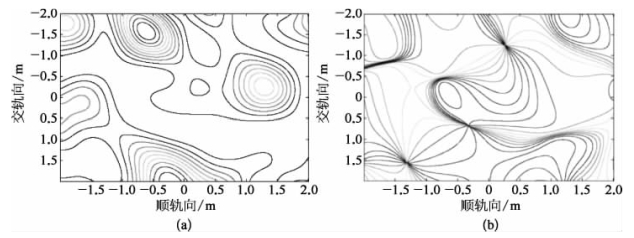
图9-5　散斑等强度线和等相位线图

（a）等强度线；（b）等相位线

图9-5（b）是散斑等相位线图，共有10条间隔为π／5的相位等值线围绕这些强度零点旋转。定义相位绕强度零点转动这一现象称为涡旋［3］，逆时针旋转的涡旋为正涡旋，顺时针旋转的涡旋为负涡旋。根据定义可以看出图9-5（b）中相位围绕强度零点旋转的情况，正负涡旋成对存在，每一个涡旋邻近处的涡旋符号相反，原因是：散斑场分布为=R+iI，散斑强度为Ι=R2+I2，相位值。只有当实部和虚部同时为0（即R=I=0）时，才会出现强度零值点。由于实部和虚部正负关系的不同，导致相位值随实部、虚部的变化而围绕强度零点旋转，形成涡旋。涡旋效应导致顺轨向上光学接收天线积分后散斑引入的相位起伏变大，从而影响SAIL顺轨向成像。