光电流的本质是相干光的统计过程，该过程实际上是一个泊松过程。噪声可以定义为瞬时光电流与其数学期望之差平方的平均值。散粒噪声限由光电转换时产生的随机电流脉冲引起。对于一个恒定功率的入射光，散粒噪声和光电流的均方根值相等，可以通过时域上的平均值与方差和频域上的谱密度来表示。

对于PIN光电管，光电管所产生的光电流为一个泊松分布。光电流i（t）在频域上的谱密度可以表示为［4］

式中，λ为单位时间内光电子数目的平均值，q为电子电荷，传递函数Hd（ξ）为探测器电流冲击响应hd（t）的傅里叶变换。

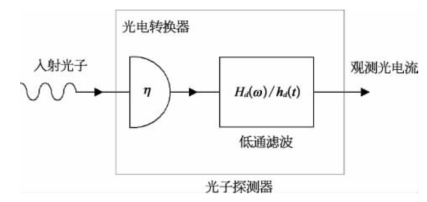
图8-3　光电探测模型

对于APD探测器，光谱密度函数可以表示为［4］

式中mg和分别为APD倍增因子g随机变化的均值和方差，随机变化的均值定义为G=mg，均方根表示为。

光电管可以通过等效电路来表征，其中电路的电阻电容（RC）部分决定器件的频率响应。因此，传递函数为

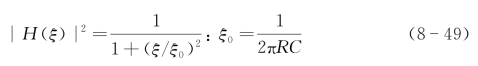
光接收机中存在的噪声主要有6部分［5］，包括量子散粒噪声、光过剩噪声、光背景噪声、光电探测器暗电流噪声、光电管过剩噪声和电子噪声。SAIL被认为在光子受限状态下工作，主要的噪声源是来自总光子数的散粒噪声。因此，PIN的简化噪声模型如图8-4所示，APD的简化噪声模型如图8-5所示。(www.daowen.com)

对于直视SAIL，由于信号光电流中的直流分量可能小于直流暗电流，所以主要散粒噪声来自暗电流。在平衡探测器里使用两个暗电流均为Id的PIN管，噪声的直流分量可以表示为In=2Id。因此噪声的功率谱可以表示为

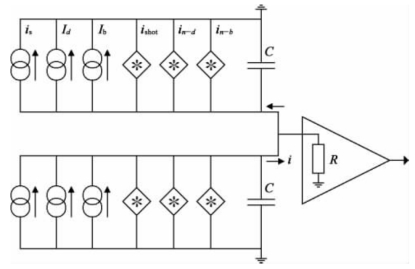
图8-4　PIN的简化噪声模型

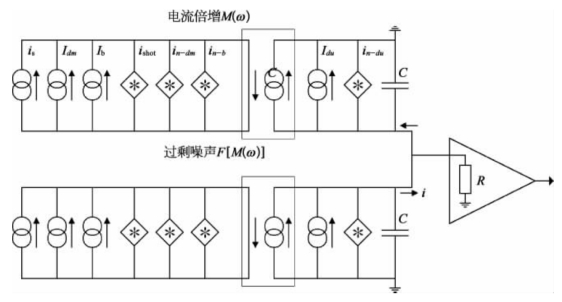
图8-5　APD的简化噪声模型

在平衡探测器里使用两个未倍增暗电流均为Idu和倍增暗电流均为Idm的APD探测器，接收机的噪声直流分量可以表示为，其中，=Idu／M+F（M）Idm／M。因此，等效输入噪声功率谱为

对于侧视SAIL，由于信号光电流中的本振直流分量可能大于直流暗电流，因此主要的散粒噪声来自本振光电流。对于PIN平衡探测器，噪声的直流分量In可以表示为In=IL。因此，噪声的功率谱为

对于APD平衡探测器，接收机的噪声直流分量In可以表示为In=，其中，=ILF（M）／M。因此，等效输入噪声功率谱为