光学正透镜的前焦面上放置透射物体则在后焦面上能够得到输入物体的傅里叶变换频谱，因此对于任意相位分布函数，本节提出在光学傅里叶变换系统中采用准几何近似来得到它的傅里叶变换解析近似解的概念。准几何方法是指采用光线偏折投影传输来研究后焦面上的分布，而不是傅里叶变换所定义的输出是输入函数的全域积分结果。

本节首先给出一维有限宽度相位函数的准几何光学傅里叶变换的一般性操作过程，据此推导了有限宽度相位二次项、相位三次项傅里叶变换的近似解析解，可以看到它与稳相法（见附录A）的结果完全一致，证明了准光学方法的可行性。

上述所有有限宽度相位函数傅里叶变换的近似解析解可以简单地推广到任意相位函数无限宽度的傅里叶变换解，即假定振幅或者窗口函数恒定为1。

准几何光学傅里叶变换方法也可以直接推广到二维相位物体。在物理上比较形象，能够直接理解相位物体产生的频谱过程。

1）光学傅里叶变换原理

本节中的光学傅里叶变换原理源自古德曼的著作［6］，采用单一正透镜可以实现傅里叶变换，在理想状态下，透镜焦距为f，在前焦面上输入函数为s（x，y），在后焦面可以得到它的傅里叶变换S（ξ，η），即理想系统假设下有

式中，E为光场强，1／（jλf）为光学系统引入的长度比例因子。

上述二维光学傅里叶变换系统可以退化为一维光学傅里叶变换系统，在一维状态下前焦面和后焦面函数为光学傅里叶变换：

其中为光学系统引入的长度比例因子。一维有限宽度相位二次项为一维函数，因此必须在一维光学傅里叶变换系统中操作。

2）一维相位函数光学傅里叶变换的准几何光学近似方法

相位变化物体的准几何光学近似是基于光线通过该物体时产生光线的角度偏折［7］。一维相位函数记为exp［jφ（x）］，则光线通过x点产生的偏折角θ1为

如图6-9所示，因此作为光学傅里叶变换系统的输入点A，它通过透镜B点后将到达后焦面的C点，其坐标位置为

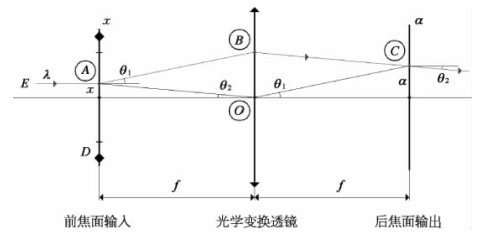
图6-9　准几何光学傅里叶变换原理

输入点A相对于透镜中心点O的视角θ2为

因此光学传输路径A-B-C与入射视场方向O-A和出射视场方向O-C构成一个平行四边形A-B-C-O，出射光线偏折角为-θ2，即偏折为-tanθ2（x）。

为了求得有限宽度一维相位函数光学傅里叶变换，必须求得如下函数因子：

（1）场强比例因子。定义为前焦面x点位置上Δx的微小尺度在后焦面α点位置上Δx的变化尺度之比，即

（2）振幅函数的坐标变换。即

对于窗口宽度函数有

（3）后焦面上相位因子。后焦面α点位置上的光线偏折角为θ2（x），需要首先将坐标x转化为坐标α，即

然后几何求得后焦面上的相位函数，即

（4）准几何光学的近似傅里叶变换即为

为了从光学傅里叶变换中消除场强因子和变换透镜焦距因子得到纯傅里叶变换，还要作如下处理：

（1）从空间坐标变为频谱坐标，这样能够自然消除透镜的焦距因子而获得傅里叶变换表达，即替代变换为

（2）为了消除光学变换的场强因子，需要乘上因子。

最终，一维有限宽度相位函数的准几何光学近似傅里叶变换的结果为

同样，当窗口函数rect（x）≡1时，上述有限宽度相位函数傅里叶变换的近似解析解可以简单地推广到该相位函数在无限宽度时的傅里叶变换解。

上述表达中去除振幅函数或宽度函数即可以简化为一维无限宽度相位函数的准几何光学近似傅里叶变换表达，即无限宽度相位函数的傅里叶变换表达为

这提供了任何相位函数的傅里叶变换的一种简单的近似计算方法。(www.daowen.com)

3）有限宽度相位二次项的准几何光学傅里叶变换解析解

有限宽度相位二次项为，为了光学概念清晰可以采用透镜的表达方法即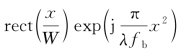，因此有偏折角：

以及

场强比例因子为

有限宽度函数的坐标变换为。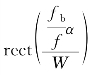

后焦面上光线偏折为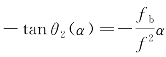，后焦面上的相位函数为积分：

准几何光学的近似傅里叶变换即为

最终得到

或者更为一般性的表达为

事实上，一个相位二次项即一个透镜在傅里叶变换透镜后焦面上会产生离焦，它等同于后焦面上的相位函数。离焦量可以用成像公式fbfx=-f2求得，即有

这与上述结果相同。可见上述偏折角积分法求解相位分布函数方法是可行的。

4）有限宽度相位三次项的准几何光学傅里叶变换解析解

有限宽度相位三次项为，因此有偏折角：

以及

这里可以看出无论x为正或负，α永远为负（A为正）或者α永远为正（A为负），即该函数的频谱是单边带的。需要分两部分即（x＞0）或者（x＜0）进行分析。

（1）对于（x＞0）部分。

场强比例因子包括光场因子消除为

其存在条件为

应当注意x=0为奇点，因为这时。

有限宽度函数的坐标变换为。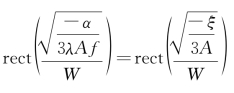

后焦面上光线偏折为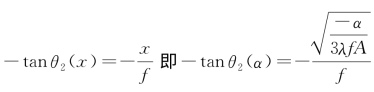，后焦面上的相位函数为积分：

因此得到

（2）对于（x＜0）部分。

同样可以得到

因此最终解为

或者