在真空环境下传输到距离z处的光波场根据傍轴近似表示为

在湍流中，上式变为

称为广义的Huygens-Fresnel原理傍轴近似表达式，其中χ和S分别是湍流影响的振幅项和相位项。由于湍流的随机起伏导致χ和S也分别是随机变量，按照统计场的处理方法，对它们的描述一般仍采用结构函数D或相关函数B来表示。对于相位起伏而言，其结构函数DS（ρ，L）和相关函数BS（ρ，L）分别为

对于各项同性的均匀介质，相关函数和结构函数的描述是等价的，由于是对光波内两点间相位起伏相关程度的统计描述，因此它们经常用于定义光波的相干长度以及计算到达角起伏等。对于涉及光强起伏和像点抖动等光场性质的卫星激光通信应用时，可采用结构函数或相关函数进行分析。然而，对于涉及光学相干处理的合成孔径激光雷达等应用时，需要分析大气湍流对接收光场引入的相位误差，因此必须对相位起伏方差进行分析。

当平均相位差为0，即ρ=0时相位起伏的相关函数其实就是单点上的相位起伏方差：

假设传播路径上湍流谱具有相同形式，即均为kolmogorov谱或von karman谱，则对于平面波，单点相位起伏方差为

式中，f（Kl0）为湍流谱的修正因子项。而球面波的单点相位起伏方差为

可以看出，单点相位起伏方差与湍流谱低频端的形状关系密切。若采用von Karman湍流谱，则平面波的单点相位起伏方差可积分得到

球面波的单点相位起伏方差为

随高度变化的模型通常采用应用较为广泛的Hufnagel-Vally湍流廓线模型：

式中，H为终端海拔高度，的典型值为1.7×10-14m-2／3，v为风速的均方根（RMS）值：

式中，V（H）为Bufton风速模型：(www.daowen.com)

式中，ωs为卫星终端相对于地面观测站的转动速率，vg为地面的风速。在实际的测量中，对于圆形孔径上的相位起伏方差，有

其中，F（γκ）=G（γκ）G*（γκ）为孔径接收较点接收多出的修正因子，G（γκ）为孔径函数的傅里叶变换，它可以表示为Zernike多项式的函数形式。

事实上，由于Zernike多项式在圆域上的正交性，在自适应光学等天文光学应用领域内广泛使用Zernike多项式表征大气湍流为光波波前引入的相位误差。Zernike多项式是在圆域上对径向变量和角度变量的连续函数正交的二维多项式。Zernike多项式的描述较多，形式略有差别，比较通用的是结合Noll的表示法将二维的Zernike多项式表示成只有一个阶次的形式。具有不同阶次值的Zernike多项式分别表征了不同的湍致波前像差，其中1阶对应于波前的整体移动，称为活塞项（piston），2阶和3阶对应于两个正交方向上的倾斜（tip／tilt），也叫线性项，4阶为散焦项（defocus），5阶和6阶对应于像散（astigmatism），散焦和像散也叫二次项，这些低阶项反映了波前的傍轴性质；7阶和8阶对应于慧差（coma），9阶和10阶对应于三瓣叶状像差，11阶及以上对应于各级球差等高阶像差。

在半径为R的圆接收孔径内，湍流导致的畸变光波波前为

根据Zernike的正交特性，可求得各项系数为

当已知各阶Zernike多项式的系数后，可在单位圆域内求得波前的方差为

因此，对于倾斜、散焦和像散等3种常见的低阶像差，有

式中，为波前倾斜的参数，D为接收孔径，r0=为传输的大气相干长度，为波前倾斜相位方差。

对于尺寸为D的孔径接收，若大气湍流累计作用后的大气相干长度为r0，则接收孔径内的总的光波波前相位起伏方差可近似表示为

式中，线性项引起的波前倾斜量为，在解析公式分析中，引入的线性倾斜项表示为，其中x=D／2，令，则波前倾斜角。而二次项引起的波前曲率量为，在解析式分析中，引入的二次曲率项表示为，则引入的波前曲率半径为。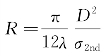

前述分析可以得出3个主要的结论：第一，尽管合成孔径处理过程对于大气湍流导致的光程差变化非常敏感，然而对于光学波段在湍流介质中却是可行的；第二，湍流对合成孔径激光雷达的交轨向分辨率没有影响；第三，合成孔径激光雷达的顺轨向分辨率总是由相干长度为的球面波经过去斜处理后的结构函数确定，大气湍流的折射率结构参数分布的高阶矩以及权重并不影响雷达的成像分辨率。