1）结构和原理

交轨向单棱镜转动方式是在交轨向上采用单棱镜进行转动实现交轨向的线性相位调制，两入射光束经过棱镜折射后产生空间波面相位，其波面变换操控物理模型如图5-10所示，由该模型可获得其棱镜偏折角等效相位面表达。

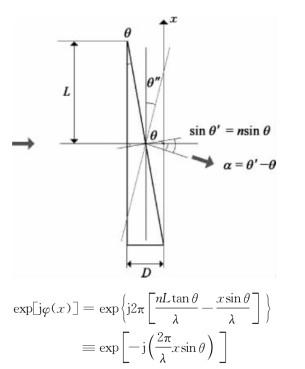
图5-10　旋转单棱镜的波面变换操控物理模型

单棱镜的折射角α可以通过下式获取：

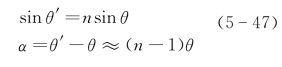
式中，n为单棱镜的折射率，θ为单棱镜的顶角，θ′为出射光束与单棱镜斜面法线的夹角，由折射角求得倾斜波面相位表达式为

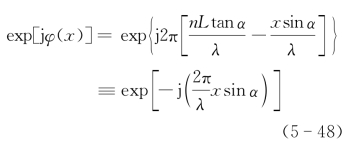
式中，2L为单棱镜的入射面直径，λ为入射光的波长。

2）分析

旋转单棱镜在这个透射式等光程反光场双臂偏振复合干涉结构中的两个窗口中的光程如图5-11所示。

单棱镜沿棱镜中心旋转的旋转角为θ（tn，f），初始时刻θ=0，tn，f=0，且棱镜的顶角写为θp。左通道内光场窗口中心与单棱镜旋转中心线的垂直距离为

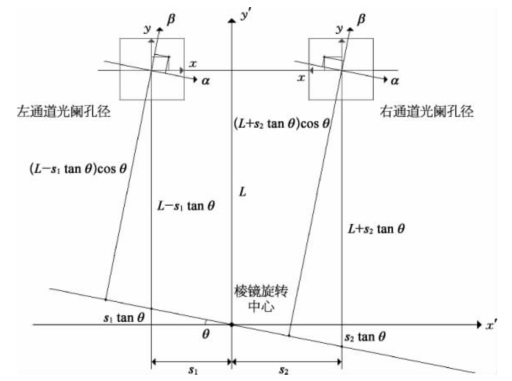
图5-11　透射式旋转棱镜的波面变换操控物理模型

式中，L为棱镜旋转中心与左右通道中心连线的垂直距离，s1为左通道中心与y′轴的垂直距离。在光场窗口内的（x，y）点在旋转的β-坐标系上的投影为β=x sinθ+y cosθ。

因此，（x，y）点等于棱镜旋转中心线的距离为

左通道棱镜的相位方程为(www.daowen.com)

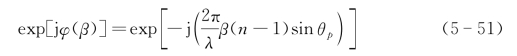
最终左通道经过棱镜后的光场相位为

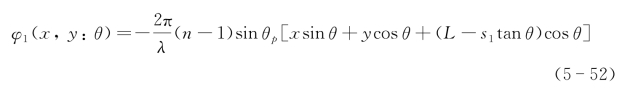
同理，右通道内光场窗口中心相对于棱镜旋转中心线的距离为

同理，（x，y）点等于棱镜旋转中心线的距离为

棱镜的相位方程为

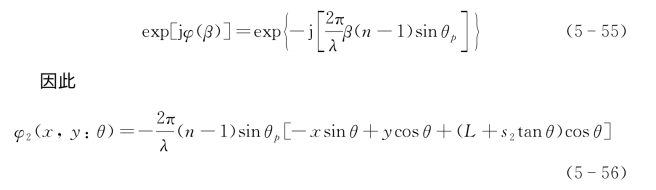
所以交轨向相位差调制函数为

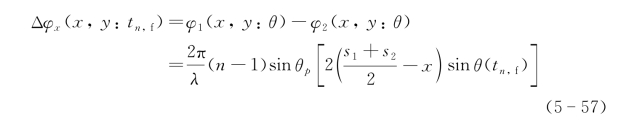
在线性近似下，有

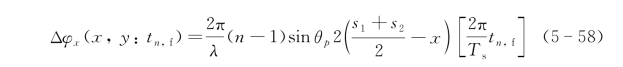
角度旋转速度为

线性相位项调制函数为

这样即获取了交轨向相位线性项调制。其顺轨向的调制与前两种相同，不再讨论。