当发射望远镜采用圆孔径时，如图3-5所示。圆孔径望远镜的物镜和目镜瞳孔均为圆孔，物镜直径为Dt时的孔径函数为

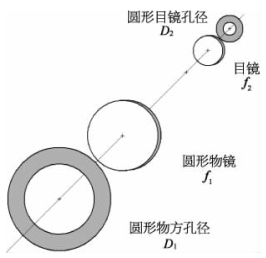
图3-5　圆孔径望远镜结构

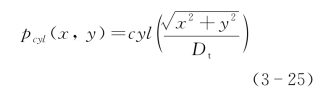
因此不论作为接收或者发射，其相应的方向性函数在目标面上有［1～5］

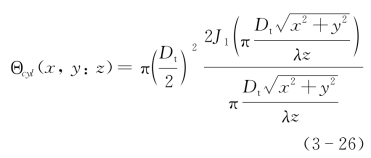
其中主瓣的直径为d0=2.44λz／Dt。

式（3-7）中的Kt，x（x）和Kt，y（y：n Ts）应表示为

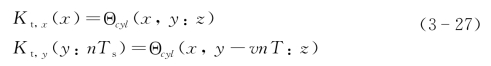
圆形孔径SAIL最终的二维数据收集方程与矩形孔径SAIL一致，见式（3-18），区别在于外差方向函数不同，外差接收方向性函数Θ（xp，yp-vn Ts）为

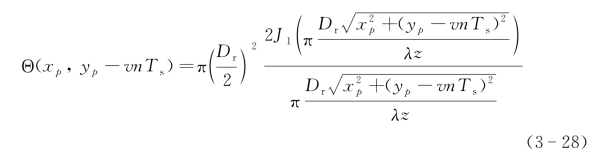
圆形孔径SAIL交轨向的成像分辨率也完全一样，见式（3-22），但顺轨向的成像分辨率与矩形孔径SAIL存在较大的差别。

同样，顺轨向的分辨率与脉冲响应有关，计算中需要对二维艾里斑进行顺轨向的一维傅里叶变换。但运算中对于二维的艾里斑函数进行一维截取的傅里叶变换没有解析解，本节进行近似估算，通过数值计算结果的比较可以看到在艾里斑半径左右，二维艾里斑函数的一维剖面函数能够近似表达为

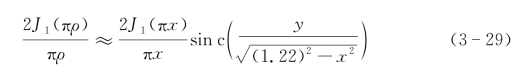
式中，。

其傅里叶变换为

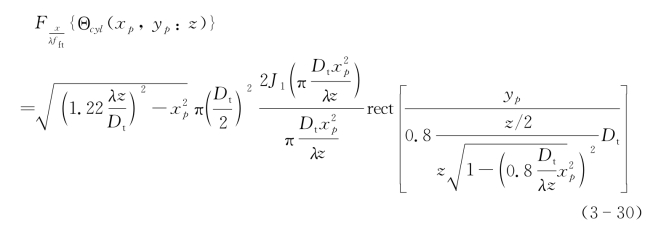
假设Dt=Dr=D，最终得到圆形孔径天线的SAIL成像的顺轨向PSF为（忽略常数项）

式中，L为匹配滤波器宽度，Δy为顺轨向采样间隔，m为顺轨向采样序列。从式（3-31）可以看出顺轨向分辨率与交轨向位置xp相关。

在匹配滤波无失配和无限大窗口的条件下，式（3-31）可化简为

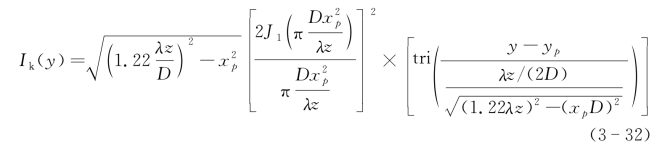
定义这种情况的顺轨向分辨率为理想分辨率。(www.daowen.com)

从PSF得到的是三角形剖面分布，像点零值全宽为

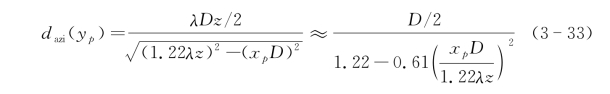
首先考虑运动中心线上的像点尺寸，此时xp=0的像点零值全宽为

可见，圆孔激光合成孔径雷达在中心线上的理想分辨率为0.4D，小于矩形孔径合成孔径雷达顺轨向分辨率0.5D。

目标点在垂直偏离中心线扫描位置（xp≠0）上产生的顺轨向分辨率影响可以根据上述公式用如下扩大因子表达：

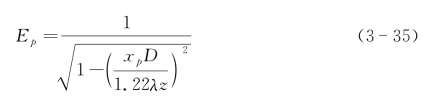
可见扩大1.5倍分辨率尺寸的垂直方向中心偏离为0.75艾里半径。

当空间相位匹配滤波器曲率半径偏离理想值时，会造成顺轨向成像分辨率下降，空间相位匹配滤波器的失配效应可以简化为

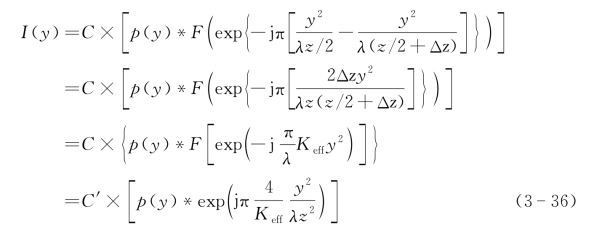
式中，C和C′是常数，p（y）为理想成像PSF，底宽为dy，定义Keff为等效曲率：

可以用稳相法求得失配加宽的成像点零值全宽度的近似解析表达式。最终可求得分辨率尺寸为

因此克服失配所要求的匹配滤波器条件为

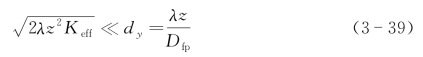
顺轨向数据收集的空间宽度（L）也就是聚焦成像傅里叶变换的积分宽度，空间积分带宽的影响等效于基本成像PSF与带宽响应函数sin c［Lx／（λfft）］的卷积。空间带宽等于圆形光学足趾的艾里斑直径L=2.44λz／D时，可以作为窗口宽度的判据，即

以顺轨向相邻采样的相位变化为π作为判据，得到顺轨向采样间隔须满足：

当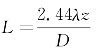时，顺轨向采样间隔有