发射光场的时间相位可以表示为

假设雷达沿顺轨向运动，运动速度为v，激光光源的平均波长为λ，到达目标面的光场复振幅为

式中，τp=2（Z+zp）／c是双程时延，Kt代表发射光场的方向性函数，与发射口径和发射光场有关。

假设目标尺寸为lx×ly，中心坐标在（xp，yp），目标反射率为ρp，可以导出目标面回波在雷达接收平面的光场分布为

式中，Kr，x（x：xp）=Kr，x（x-xp），Kr，y（y：yp：n Ts）=Kr，y［y-（ypvn Ts）］。Kr，x（x：xp）和Kr，y（y：yp：n Ts）为目标区域复散射特性和信道随机干扰等因素决定的附加复振幅项。在此，暂不考虑，因此式（3-9）可简化为

假设本振光场的空间波面为平面波，时间相位与发射激光相同但有不同时延，可以表示为

经过本振光和回波信号光外差相干探测后，得到的交流信号为

式中，τlo为本振光的时延，本振光与回波信号的时延差，表示为Δτp=τp-τlo。当Δτp很小时，发射信号源的频率调谐线性度的影响可以忽略。

为了简化，将所有的光场衰减记为η。接收到的光功率为接收光强在接收望远镜口径内的二维积分，假设接收口径尺寸为，不考虑探测器损失，外差信号可以表示为

式中，Θ（xp，yp-vn Ts）为外差接收方向性函数，表示为

从接收外差信号表达式可以看出，接收信号的强度不仅与发射光场的方向性函数有关，还与接收外差探测的方向性函数有关，两者共同决定了合成孔径激光成像雷达的光学足趾。

光电平衡探测器将光信号转化为电流信号，数字化时的采样时间长度为Tf，采样时间长度应小于脉冲持续时间。假设时域采样窗口为矩形窗，时域采样窗口函数可以表示为rect｛［tn，f-（τp+Tf／2）］／Tf｝。

采用2×4 90°光学桥接器接收，将外差中频信号复数化，考虑到时间采样窗口函数，点目标的雷达方程可以写为(www.daowen.com)

Ks是与系统结构有关的因子。

最终，合成孔径激光成像雷达的二维数据收集方程为

从数据收集方程可以看出，降低时间采样窗口长度可以降低非线性啁啾和时域散斑的影响。

根据数据收集方程，先经过交轨向的一维傅里叶变换和顺轨向匹配滤波，可以得到二维的SAIL图像，表示为

对于点目标，上式可简化为

式中，SR（ξ）是交轨向成像的脉冲响应函数，SA（m）是顺轨向成像的脉冲响应函数。*代表卷积运算。在目标平面上有

在理想情况下，交轨向的脉冲响应为sin c（ξTf），与数据采集时间长度有关。理论上，交轨向半高全宽理论分辨率为

式中，B为SAIL激光光源快时间数据采集时间内的调频带宽。

同样，顺轨向的脉冲响应表示为sin c｛yDft／［λ（Z／2）］｝，与SAIL的光学足趾尺寸Dfp有关，顺轨向零值全宽理论分辨率为

当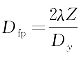时，上式可进一步写为