本节提出了SAIL的二维傅里叶变换成像算法，即对于回波信号进行顺轨向相位二次项历程共轭补偿后直接实施二维傅里叶变换，其特点是把交轨向和顺轨向的二维时间域数据均直接变换到二维频率域的成像输出数据。在此基础上，给出了矩形和圆形孔径的SAIL随交轨向变化的顺轨向成像分辨率解析表达式，结果表明圆形孔径的顺轨向成像分辨率从目标面中心随交轨方向向外逐渐变坏。

合成孔径激光成像雷达的二维傅里叶变换成像算法对所获得的时间函数数据流先进行顺轨向共轭相位二次项补偿，然后进行二维傅里叶变换。二维傅里叶变换的时间坐标为，其中为等效慢时间，而为等效快时间。傅里叶变换窗口宽度为。等效慢时间在回波数据流上的启动时间为ts（K）［-∞≤ts（K）≤∞］，其中定义ts（K）-ts，上述的时间关系和变换关系如图2-7所示。

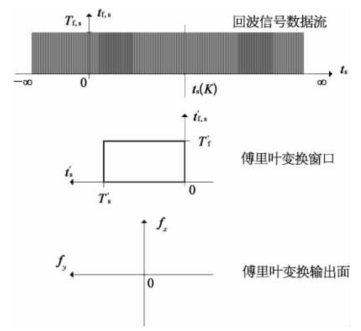
图2-7　傅里叶变换采样窗口与回波信号数据流的关系

共轭相位二次项为

SAIL的光学足趾在矩形孔径时为或者在圆形孔径时为Dfp，应当注意在顺轨向的经历时间为

因此当=2Ts时，该算法对于顺轨向光学足趾的两倍数据进行变换，输出将得到二维图像函数。因此二维成像输出为傅里叶变换：

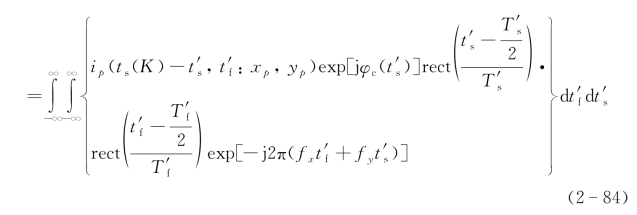
最大截止频率为。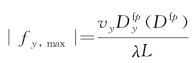

当时，输出像必须定义在fy=0的一维表达上，即有

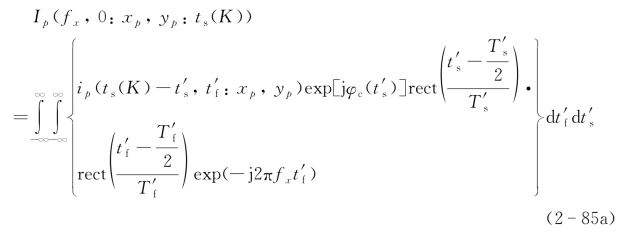
最终，相对于目标点（xp，yp）的输出像为

1）侧视SAIL的二维傅里叶变换成像算法的物理过程

（1）矩形孔径侧视SAIL的成像。

光学发射／接收口径为Dx×Dy，则光学足趾尺寸为2λZ／Dy（零值全宽），考虑了发射光斑和外差接收方向性的光学足趾函数为

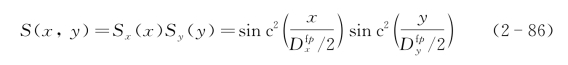
侧视SAIL在结构设计中已经定义了顺轨向分辨率（零值全宽度）为dy=Dy／2，交轨向分辨率（零值全宽度）为，一般要求dx=dy则有=c／DyTf。

因此，傅里叶变换后的成像信号为：

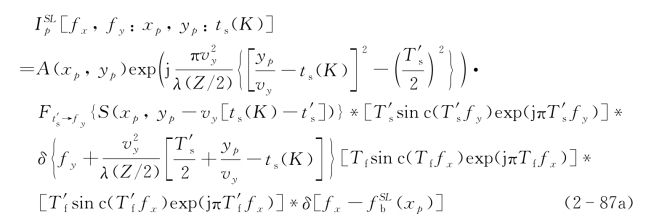
式中符号*表示卷积，其中光学足趾函数的一维傅里叶变换为

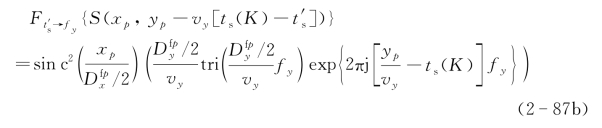
首先讨论顺轨向的成像位置和成像分辨率，由式（2-87a）前一个卷积项表示的顺轨向成像函数可以看到顺轨向成像点位置为

光学足趾函数的一维傅里叶变换决定了顺轨向成像分辨率，其中卷积相当于点扩散函数，其宽度代表成像分辨率，即Δfy，1=2Dyvy／（λZ）=4vy／Dfp（零值全宽）。而傅里叶变换窗口的宽度为（零值全宽）。因此顺轨向成像宽度近似为

式（2-87a）后一个卷积项表示交轨向成像函数，交轨向成像点位置可见为

应当注意侧视SAIL中是单极性的，所以成像只在顺轨向一侧。交轨向成像点的系统设计宽度为Δfx，1=2／Tf，而傅里叶变换窗口尺度决定的成像宽度为（零值全宽）。两个sin c函数的卷积仍然是sin c函数，因此交轨向成像宽度（零值全宽度）最终为

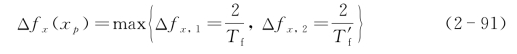
（2）圆孔径侧视SAIL的成像。

圆孔径侧视SAIL成像过程与矩形孔径一致，只需改变光学足趾函数的一维傅里叶变换及其顺轨向分辨率。为了得到近似解析分析，对于二维光学足趾函数可以给出近似表达：

这种近似保持了在x轴和y轴上的函数准确分布，同时第一级零点具有准确的半径Dfp／2。所以

因此对于的傅里叶变换为

显然在顺轨方向上的成像分辨率的零值全宽度为

可以看到由于圆分布函数，在xp=0上由于合成孔径积分长度最大而达到最高成像分辨率，宽度为Δfy（min）=4vy／Dfp。但是随着xp的增加成像分辨率降低，在边缘上因为合成孔径积分长度接近零而分辨率宽度趋向无穷大。

2）直视SAIL的二维傅里叶变换成像算法的物理过程

（1）矩形孔径直视SAIL的成像。(www.daowen.com)

矩形孔径直视SAIL的光学足趾函数是矩形函数，有

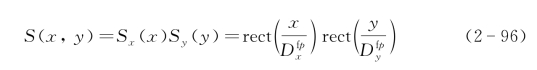
直视SAIL在结构设计中已经定义了交轨向成像分辨率（零值全宽）为dx=（柱面透镜扫描），dx=λ／（2ΔΘ）（反射镜扫描），顺轨向成像分辨率（零值全宽）为。

成像算法的第一步是对于数据流进行顺轨向二次项相位补偿，然后进行二维傅里叶变换。因此傅里叶变换后的成像信号为

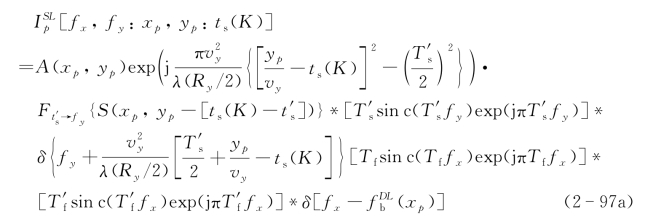
其中光学足趾函数的傅里叶变换为

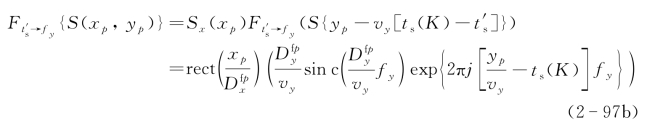
首先讨论顺轨向的成像位置和成像分辨率。由式（2-97a）前一个卷积项表示顺轨向成像函数，可以看到顺轨向成像点位置为

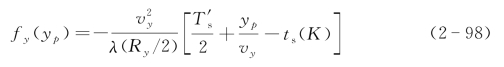
光学足趾函数的一维傅里叶变换决定了顺轨向成像分辨率，其中宽度代表成像分辨率，sin c（Dfpfy／vy）的宽度为Δfy，1=2vy／Dfp（零值全宽），而的宽度为（零值全宽），因此顺轨向成像宽度为

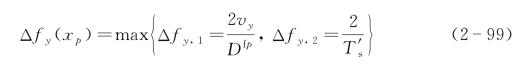
式（2-97a）后一个卷积项表示交轨向成像函数，交轨向成像点位置可见为

应当注意直视SAIL在直视观察时，是双极性的，所以成像在顺轨向两侧。交轨向成像点的系统设计宽度为Δfx，1=2／Tf，而傅里叶变换窗口尺度决定的为成像宽度为（零值全宽），因此交轨向成像宽度（零值全宽）最终为

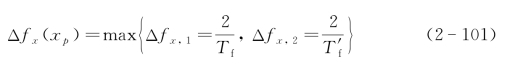
（2）圆孔径直视SAIL的成像。

圆孔径直视SAIL成像过程与矩形孔径一致，只需改变光学足趾函数的一维傅里叶变换及其顺轨向分辨率。为了得到近似解析分析，对于二维光学足趾函数可以给出近似表达：

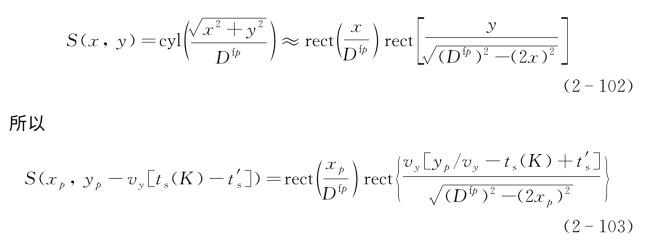
因此对于的傅里叶变换为

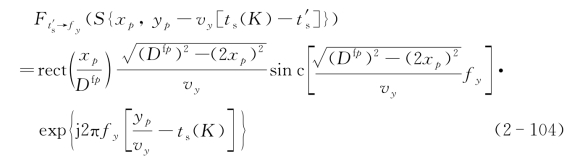
在顺轨向上的成像分辨率的零值全宽度为

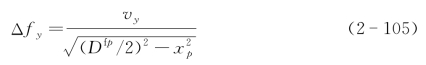
可以看到由于圆分布函数，在xp=0上由于合成孔径积分长度最大而达到最高成像分辨率，宽度为Δfy（min）=2vy／Dfp。但是随着xp的增加成像分辨率降低，在边缘上因为合成孔径积分长度接近零而分辨率宽度趋向无穷大。

3）算法的离散傅里叶变换表达

SAIL的回波数据都是离散化采样取得的，二维傅里叶变换成像算法最终是采样离散傅里叶变换［7］实现的，综合分析了算法的离散傅里叶变换表达。

设定k为顺轨向慢时间采样序列，根据采样定理慢时间采样周期应至少为

因此光学足趾内的慢时间采样数为

交轨向的最大差频频率为，根据采样定理快时间采样周期至少为因此快时间采样数为

参考式（2-74），侧视或者直视SAIL对于第p个目标点得到的回波二维数据可以用时间系列指数表达为ip（k，n（k）：xp，yp）。参考图2-7，令慢时间上的离散傅里叶变换的启动时间指数为K，离散傅里叶变换的窗口函数的时间序列指数为n×m，其中快时间序列指数为n=0，1，…，（N-1），慢时间序列指数为m=K-k，取k=K，K-1，K-2，…，K-（M-1），则m=0，1，2，…，M-1。为方便起见，设定M和N均为奇数。

离散傅里叶变换窗口中的相位二次项补偿函数为

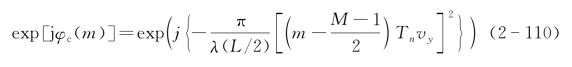
因此离散傅里叶变换后的二维成像输出为

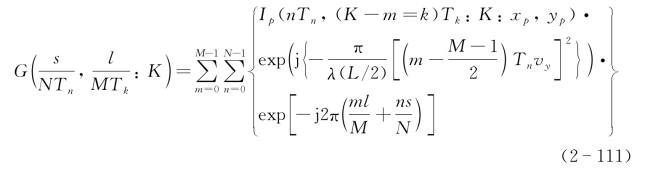
式中，

对于处理图像的二维输出或者一维输出的傅里叶变换窗口宽度的要求，同样地当M=2M′时算法对于顺轨向光学足趾的两倍数据进行变换，将直接得到二维图像输出，而当M=M′时算法对于顺轨向光学足趾的一倍数据进行变换，输出像必须定义在l=0的一维表达上。

4）结论

本节提出了侧视和直视合成孔径激光成像雷达的二维傅里叶变换成像算法，即对于回波信号进行顺轨向共轭相位二次项共轭补偿后直接实施二维傅里叶变换。本节采用连续函数对于矩形和圆形孔径的侧视和直视SAIL进行了算法成像验证，并且分析了矩形和圆形孔径下的成像分辨率，最后给出了离散傅里叶变换的表达形式。本算法的特点是把交轨向和顺轨向的时间域信号数据均直接变换到频率域的成像输出数据，对于侧视和直视SAIL提供了一种新的成像算法。

应当特别注意的是本节给出了圆形孔径SAIL的随交轨向变化的顺轨向成像分辨率的解析表达式，表明顺轨向成像分辨率从目标面中心向外逐渐变坏。因为二维傅里叶变换成像方法和以前的匹配滤波成像算法在物理上是一致的，因此这种顺轨向成像分辨率表达也适用于匹配滤波成像算法。

匹配滤波算法的顺轨向处理是直接在时间域对于相位历程信号进行共轭二次项匹配滤波，而在本算法中顺轨向傅里叶变换处理相当于在频率域中对于相位历程信号谱进行共轭二次项谱的匹配滤波，在信号和信号谱的两个定义域中进行相同的运算却在这两个不同域中得到了完全相同的成像结果，核心原因是相位历程必须是相位二次项，这也进一步证明了SAIL孔径合成的本质是顺轨向上的相位二次项产生。