1）一般性分析

设采用外差探测时，目标回波光场复振幅为

假设本振光为平面波，其复振幅可表示为

式中，

本振光和回波光相干探测后，输出的交流分量为

式中，

对探测面进行积分，可得

其中，若假定积分面积S是中心对称的，在平行光外差探测下Δφ（x，y）具有共轭中心对称（厄米型）性质即倾斜平面波。所以积分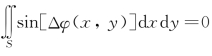，可以忽略不计。

外差探测的方向性函数与积分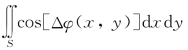有关。

（1）使用矩形孔径，分离变量坐标体系下，积分面积S为Dx×Dy，有外差探测方向性函数为

（2）使用圆形孔径，同样中心复对称，积分面积S为圆孔径，其直径为Dr，有外差探测方向性函数为

其中采用了公式：

及2r0=Dr，即最终圆孔外差方向性函数为

探测面上本振光束垂直入射，回波光束偏角为θ。根据圆对称关系可以假设沿x方向偏转，其归一化干涉条纹的光强为(www.daowen.com)

光电探测器直径为d，则接收能量为积分：

可以得到：

条纹积分能量对比度，即光学外差接收方向性函数，可以定义为ψ=，因此光学外差接收方向性函数为

折算到口径为D的望远镜主镜入瞳，光学外差接收方向性函数为

因此接收视场角为

2）二次相位波面的外差探测效率

探测面上本振光束为垂直入射的平面波，回波为二次项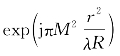，R

为望远镜入瞳的回波波面曲率半径。因此归一化干涉强度为

以方形接收口径为例，在口径d内的积分能量为

球面波产生的外差探测效率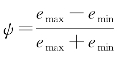，则有

折算到口径为D的望远镜主镜入瞳，球面波产生的外差探测效率函数为

因此ψ=0的消光曲率半径为